Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lipatnikov, A.N.
Sabelnikov, V.A.
Hernández-Pérez, F.E.
Song, W.
and
Im, Hong G.
2020.
A priori DNS study of applicability of flamelet concept to predicting mean concentrations of species in turbulent premixed flames at various Karlovitz numbers.
Combustion and Flame,
Vol. 222,
Issue. ,
p.
370.
Lipatnikov, Andrei N.
and
Sabelnikov, Vladimir A.
2020.
An extended flamelet-based presumed probability density function for predicting mean concentrations of various species in premixed turbulent flames.
International Journal of Hydrogen Energy,
Vol. 45,
Issue. 55,
p.
31162.
Lipatnikov, A. N.
Nilsson, T.
Yu, R.
Bai, X. S.
and
Sabelnikov, V. A.
2021.
Assessment of a flamelet approach to evaluating mean species mass fractions in moderately and highly turbulent premixed flames.
Physics of Fluids,
Vol. 33,
Issue. 4,
Darragh, Ryan
Towery, Colin A. Z.
Meehan, Michael A.
and
Hamlington, Peter E.
2021.
Lagrangian analysis of enstrophy dynamics in a highly turbulent premixed flame.
Physics of Fluids,
Vol. 33,
Issue. 5,
Yu, R.
Nilsson, T.
Fureby, C.
and
Lipatnikov, A.N.
2021.
Evolution equations for the decomposed components of displacement speed in a reactive scalar field.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Lipatnikov, A.N.
and
Sabelnikov, V.A.
2021.
Evaluation of mean species mass fractions in premixed turbulent flames: A DNS study.
Proceedings of the Combustion Institute,
Vol. 38,
Issue. 4,
p.
6413.
Sabelnikov, V. A.
Lipatnikov, A. N.
Nishiki, S.
Dave, H. L.
Hernández Pérez, F. E.
Song, W.
and
Im, Hong G.
2021.
Dissipation and dilatation rates in premixed turbulent flames.
Physics of Fluids,
Vol. 33,
Issue. 3,
Pignatelli, Francesco
Yu, Rixin
Bai, Xue-Song
and
Nogenmyr, Karl-Johan
2021.
Displacement speed analysis of surface propagation in moderately turbulent premixed reacting waves.
Physics of Fluids,
Vol. 33,
Issue. 3,
Lipatnikov, A.N.
Sabelnikov, V.A.
Hernández-Pérez, F.E.
Song, W.
and
Im, Hong G.
2021.
Prediction of mean radical concentrations in lean hydrogen-air turbulent flames at different Karlovitz numbers adopting a newly extended flamelet-based presumed PDF.
Combustion and Flame,
Vol. 226,
Issue. ,
p.
248.
Brouzet, D.
Talei, M.
Brear, M.J.
and
Cuenot, B.
2021.
The impact of chemical modelling on turbulent premixed flame acoustics.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Hatwar, Madwaraj
Nayak, Ashwin S.
Dave, Himanshu L.
Aggarwal, Utkarsh
and
Chaudhuri, Swetaprovo
2021.
Sustainable Development for Energy, Power, and Propulsion.
p.
389.
Lipatnikov, Andrei N.
and
Sabelnikov, Vladimir A.
2022.
Flame folding and conditioned concentration profiles in moderately intense turbulence.
Physics of Fluids,
Vol. 34,
Issue. 6,
Lee, HsuChew
Dai, Peng
Wan, Minping
and
Lipatnikov, Andrei N.
2022.
A DNS study of extreme and leading points in lean hydrogen-air turbulent flames - part II: Local velocity field and flame topology.
Combustion and Flame,
Vol. 235,
Issue. ,
p.
111712.
Suillaud, Edouard
Truffin, Karine
Colin, Olivier
and
Veynante, Denis
2022.
Direct Numerical Simulations of high Karlovitz number premixed flames for the analysis and modeling of the displacement speed..
Combustion and Flame,
Vol. 236,
Issue. ,
p.
111770.
Yakovenko, Ivan
Kiverin, Alexey
and
Melnikova, Ksenia
2022.
Computational Fluid Dynamics Model for Analysis of the Turbulent Limits of Hydrogen Combustion.
Fluids,
Vol. 7,
Issue. 11,
p.
343.
Yuvraj
Song, Wonsik
Dave, Himanshu
Im, Hong G.
and
Chaudhuri, Swetaprovo
2022.
Local flame displacement speeds of hydrogen-air premixed flames in moderate to intense turbulence.
Combustion and Flame,
Vol. 236,
Issue. ,
p.
111812.
Ihme, Matthias
Chung, Wai Tong
and
Mishra, Aashwin Ananda
2022.
Combustion machine learning: Principles, progress and prospects.
Progress in Energy and Combustion Science,
Vol. 91,
Issue. ,
p.
101010.
Buenzli, Pascal R.
and
Simpson, Matthew J.
2022.
Curvature dependences of wave propagation in reaction–diffusion models.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 478,
Issue. 2268,
Chakraborty, Nilanjan
Herbert, Alexander
Ahmed, Umair
Im, Hong G.
and
Klein, Markus
2022.
Assessment of Extrapolation Relations of Displacement Speed for Detailed Chemistry Direct Numerical Simulation Database of Statistically Planar Turbulent Premixed Flames.
Flow, Turbulence and Combustion,
Vol. 108,
Issue. 2,
p.
489.
Yuvraj
Ardebili, Yazdan Naderzadeh
Song, Wonsik
Im, Hong G.
Law, Chung K.
and
Chaudhuri, Swetaprovo
2023.
On flame speed enhancement in turbulent premixed hydrogen-air flames during local flame-flame interaction.
Combustion and Flame,
Vol. 257,
Issue. ,
p.
113017.
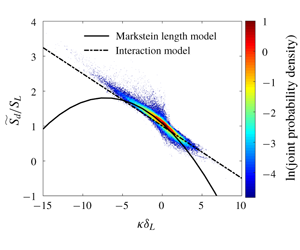
 $O(10)$. However, during the final stage of annihilation of the flame particles in the negatively curved trailing regions, the local structure of the flame no longer resembles a standard premixed flame, even qualitatively. A new interaction model for the flame displacement speed, during these final stages of annihilation of the flame elements, has been derived.
$O(10)$. However, during the final stage of annihilation of the flame particles in the negatively curved trailing regions, the local structure of the flame no longer resembles a standard premixed flame, even qualitatively. A new interaction model for the flame displacement speed, during these final stages of annihilation of the flame elements, has been derived.

