Published online by Cambridge University Press: 08 August 2012
Interaction of turbulent fluctuations with a shock wave plays an important role in many high-speed flow applications. This paper studies the amplification of enstrophy, defined as mean-square fluctuating vorticity, in homogeneous isotropic turbulence passing through a normal shock. Linearized Navier–Stokes equations written in a frame of reference attached to the unsteady shock wave are used to derive transport equations for the vorticity components. These are combined to obtain an equation that describes the evolution of enstrophy across a time-averaged shock wave. A budget of the enstrophy equation computed using results from linear interaction analysis and data from direct numerical simulations identifies the dominant physical mechanisms in the flow. Production due to mean flow compression and baroclinic torques are found to be the major contributors to the enstrophy amplification. Closure approximations are proposed for the unclosed correlations in the production and baroclinic source terms. The resulting model equation is integrated to obtain the enstrophy jump across a shock for a range of upstream Mach numbers. The model predictions are compared with linear theory results for varying levels of vortical and entropic fluctuations in the upstream flow. The enstrophy model is then cast in the form of 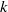 –
– equations and used to compute the interaction of homogeneous isotropic turbulence with normal shocks. The results are compared with available data from direct numerical simulations. The equations are further used to propose a model for the amplification of turbulent viscosity across a shock, which is then applied to a canonical shock–boundary layer interaction. It is shown that the current model is a significant improvement over existing models, both for homogeneous isotropic turbulence and in the case of complex high-speed flows with shock waves.
equations and used to compute the interaction of homogeneous isotropic turbulence with normal shocks. The results are compared with available data from direct numerical simulations. The equations are further used to propose a model for the amplification of turbulent viscosity across a shock, which is then applied to a canonical shock–boundary layer interaction. It is shown that the current model is a significant improvement over existing models, both for homogeneous isotropic turbulence and in the case of complex high-speed flows with shock waves.