Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T14:52:36.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Erosion of a sharp density interface by a turbulent jet at moderate Froude and Reynolds numbers

Published online by Cambridge University Press:  25 January 2018

J. Herault Open the ORCID record for J. Herault [Opens in a new window] ,
G. Facchini  and
M. Le Bars
J. Herault*
Affiliation:
Institut de Radioprotection et de Sûreté Nucléaire (IRSN), 13115 Saint-Paul-lez-Durance, France Aix–Marseille University, CNRS, Centrale Marseille, IRPHE, UMR 7342, 49 rue F. Joliot-Curie, 13013 Marseille, France
G. Facchini
Affiliation:
Aix–Marseille University, CNRS, Centrale Marseille, IRPHE, UMR 7342, 49 rue F. Joliot-Curie, 13013 Marseille, France
M. Le Bars
Affiliation:
Aix–Marseille University, CNRS, Centrale Marseille, IRPHE, UMR 7342, 49 rue F. Joliot-Curie, 13013 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using water–salt water laboratory experiments, we investigate the mechanism of erosion by a turbulent jet impinging onto a density interface, for moderate Reynolds and Froude numbers. The Froude number is defined by 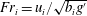$Fr_{i}=u_{i}/\sqrt{b_{i}g^{\prime }}$, with 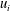$u_{i}$ and 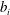$b_{i}$, the typical velocity and width of the jet at the interface, and 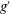$g^{\prime }$ the reduced gravitational acceleration. The Froude number 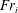$Fr_{i}$ characterizes the competition between inertial forces against the restoring buoyancy force. Contrary to previous observations reporting baroclinic destabilization of the interface, we show that the entrainment, in the range of parameters explored here, is driven by interfacial gravity waves. The waves are generated by the barotropic excitation coming from the turbulent fluctuations of the jet; they are then amplified by a mechanism of wave-induced stress; and they finally break and induce entrainment and mixing. Based on those physical observations, we introduce a scaling model for the entrainment rate, which varies continuously from 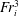$Fr_{i}^{3}$ to an 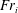$Fr_{i}$ power law from small to large Froude numbers, in agreement with the present and some of the previous laboratory data.

JFM classification

Geophysical and Geological Flows: Stratified flows Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 838 , 10 March 2018 , pp. 631 - 657
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2009 Stratified shear flow instabilities at large Richardson numbers. Phys. Fluids 21 (5), 054108.Google Scholar
Babanin, A. 2011 Breaking and Dissipation of Ocean Surface Waves. Cambridge University Press.Google Scholar
Baines, W. D. 1975 Entrainment by a plume or jet at a density interface. J. Fluid Mech. 68 (2), 309–320.Google Scholar
Baines, W. D., Corriveau, A. F. & Reedman, T. J. 1993 Turbulent fountains in a closed chamber. J. Fluid Mech. 255, 621–646.Google Scholar
Banner, M. L. & Song, J. B. 2002 On determining the onset and strength of breaking for deep water waves. Part II. Influence of wind forcing and surface shear. J. Phys. Oceanogr. 32 (9), 2559–2570.Google Scholar
Breidenthal, R. E. 1992 Entrainment at thin stratified interfaces: the effects of Schmidt, Richardson, and Reynolds numbers. Phys. Fluids 4 (10), 2141–2144.Google Scholar
Cardoso, S. S. S. & Woods, A. W. 1993 Mixing by a turbulent plume in a confined stratified region. J. Fluid Mech. 250, 277–305.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover Publications.Google Scholar
Cotel, A. J. & Breidenthal, R. E. 1996 A model of stratified entrainment using vortex persistence. Appl. Sci. Res. 57 (3–4), 349–366.Google Scholar
Cotel, A. J., Gjestvang, J. A., Ramkhelawan, N. N. & Breidenthal, R. E. 1997 Laboratory experiments of a jet impinging on a stratified interface. Exp. Fluids 23 (2), 155–160.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Ezhova, E., Cenedese, C. & Brandt, L. 2016 Interaction between a vertical turbulent jet and a thermocline. J. Phys. Oceanogr. 46 (11), 3415–3437.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23 (1), 455–493.Google Scholar
Fernando, H. J. S. & Hunt, J. C. R. 1996 Some aspects of turbulence and mixing in stably stratified layers. Dyn. Atmos. Oceans 23 (1), 35–62.Google Scholar
Fischer, H. B., List, J. E., Koh, C. R., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
Holmboe, J. 1962 On the behavior of symmetric waves in stratified shear layers. Geophys. Publ. 24, 67–113.Google Scholar
Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
Janssen, P. 2004 The Interaction of Ocean Waves and Wind. Cambridge University Press.Google Scholar
Khattab, I. S., Bandarkar, F., Fakhree, M. A. A. & Jouyban, A. 2012 Density, viscosity, and surface tension of water + ethanol mixtures from 293 to 323 K. Korean J. Chem. Engng 29 (6), 812–817.Google Scholar
Kumagai, M. 1984 Turbulent buoyant convection from a source in a confined two-layered region. J. Fluid Mech. 147, 105–131.Google Scholar
Lecoanet, D., Le Bars, M., Burns, K. J., Vasil, G. M., Brown, B. P., Quataert, E. & Oishi, J. S. 2015 Numerical simulations of internal wave generation by convection in water. Phys. Rev. E 91 (6), 063016.Google Scholar
Lighthill, M. J. 1962 Physical interpretation of the mathematical theory of wave generation by wind. J. Fluid Mech. 14 (3), 385–398.Google Scholar
Lin, C. C. 1954 Some physical aspects of the stability of parallel flows. Proc. Natl Acad. Sci. USA 40 (8), 741–747.Google Scholar
Lin, Y. J. P. & Linden, P. F. 2005 The entrainment due to a turbulent fountain at a density interface. J. Fluid Mech. 542, 25–52.Google Scholar
Linden, P. F. 1973 The interaction of a vortex ring with a sharp density interface: a model for turbulent entrainment. J. Fluid Mech. 60 (3), 467–480.Google Scholar
List, E. J. 1982 Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14 (1), 189–212.Google Scholar
Meunier, P. & Leweke, T. 2003 Analysis and treatment of errors due to high velocity gradients in particle image velocimetry. Exp. Fluids 35 (5), 408–421.Google Scholar
Miles, J. W. 1957 On the generation of surface waves by shear flows. J. Fluid Mech. 3 (2), 185–204.Google Scholar
Miles, J. W. 1960 On the generation of surface waves by turbulent shear flows. J. Fluid Mech. 7 (3), 469–478.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.Google Scholar
Morland, L. C. & Saffman, P. G. 1993 Effect of wind profile on the instability of wind blowing over water. J. Fluid Mech. 252, 383–398.Google Scholar
Phillips, O. M. 1957 On the generation of waves by turbulent wind. J. Fluid Mech. 2 (5), 417–445.Google Scholar
Shrinivas, A. B. & Hunt, G. R. 2014 Unconfined turbulent entrainment across density interfaces. J. Fluid Mech. 757, 573–598.Google Scholar
Shrinivas, A. B. & Hunt, G. R. 2015 Confined turbulent entrainment across density interfaces. J. Fluid Mech. 779, 116–143.Google Scholar
Shy, S. S. 1995 Mixing dynamics of jet interaction with a sharp density interface. Exp. Therm. Fluid Sci. 10 (3), 355–369.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Sutherland, B. 2010 Internal Gravity Waves. Cambridge University Press.Google Scholar
Woodward, P. R, Herwig, F. & Lin, P.-H. 2014 Hydrodynamic simulations of H entrainment at the top of He-shell flash convection. Astrophys. J. 798 (1), 49.Google Scholar
Young, W. R. & Wolfe, C. L. 2014 Generation of surface waves by shear-flow instability. J. Fluid Mech. 739, 276–307.Google Scholar
Yule, A. J. 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89 (3), 413–432.Google Scholar

Herault et al. supplementary movie

Mixing process in the vicinity of the interface (15 × 20cm2) The dense fluid has been dyed by rhodamine and corresponds to the bright region.

Download Herault et al. supplementary movie(Video)
Video 9.3 MB