Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T17:28:46.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Equatorial inertial instability with full Coriolis force

Published online by Cambridge University Press:  19 July 2017

R. C. Kloosterziel Open the ORCID record for R. C. Kloosterziel [Opens in a new window] ,
G. F. Carnevale  and
P. Orlandi
R. C. Kloosterziel*
Affiliation:
School of Ocean and Earth Science and Technology, University of Hawaii, Honolulu, HI 96822, USA
G. F. Carnevale
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA 92093, USA
P. Orlandi
Affiliation:
Dipartimento di Meccanica e Aeronautica, University of Rome, ‘La Sapienza’, via Eudossiana 18, 00184 Roma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The zonally symmetric inertial instability of oceanic near-equatorial flows is studied through high-resolution numerical simulations. In homogeneous upper layers, the instability of surface-confined westward currents implies potentially fast downward mixing of momentum with a predictable final equilibrium. With increasing Reynolds number, latitudinal scales along the surface associated with the instability become ever smaller and initially the motions are ever more concentrated underneath the surface. The results suggest that even if the upper layer is stratified, it may still be necessary to include the full Coriolis force in the dynamics rather than use the traditional 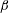$\unicode[STIX]{x1D6FD}$-plane approximation.

JFM classification

Instability: Nonlinear instability Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 69 - 108
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayly, B. J. 1988 Three dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.Google Scholar
Boyd, J. P. & Christidis, Z. D. 1982 Low wavenumber instability on the equatorial beta-plane. Geophys. Res. Lett. 9, 769–772.Google Scholar
Carnevale, G. F., Kloosterziel, R. C. & Orlandi, P. 2013 Inertial and barotropic instabilities of a free current in 3d rotating flow. J. Fluid Mech. 725, 117–151.Google Scholar
Carnevale, G. F., Kloosterziel, R. C., Orlandi, P. & van Sommeren, D. D. J. A. 2011 Predicting the aftermath of vortex breakup in rotating flow. J. Fluid Mech. 669, 90–119.CrossRefGoogle Scholar
Charney, J. G. 1973 Lecture notes on planetary fluid dynamics. In Dynamic Meteorology (ed. Morel, P.), pp. 97–351. Reidel.Google Scholar
Chiswell, S. M. 2016 Mean velocity decomposition and vertical eddy diffusivity of the Pacific Ocean from surface GDP drifters and 1000 m Argo floats. J. Phys. Oceanogr. 46, 1751–1768.CrossRefGoogle Scholar
Clark, P. D. & Haynes, P. H. 1996 Inertial instability on an asymmetric low-latitude flow. Q. J. R. Meteorol. Soc. 122, 151–181.Google Scholar
Dellar, P. J. 2011 Variations on a beta-plane: derivation of non-traditional beta-plane equations from Hamilton’s principle on a sphere. J. Fluid Mech. 674, 115–143.Google Scholar
D’Orgeville, M. & Hua, B. L. 2005 Equatorial inertial-parametric instability of zonally symmetric oscillating shear flows. J. Fluid Mech. 531, 261–291.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dunkerton, T. J. 1981 On the inertial instability of the equatorial middle atmosphere. J. Atmos. Sci. 38, 2354–2364.Google Scholar
Dunkerton, T. J. 1983 A nonsymmetric equatorial inertial instability. J. Atmos. Sci. 40, 807–813.2.0.CO;2>CrossRefGoogle Scholar
Dunkerton, T. J. 1993 Inertial instability of nonparallel flow on an equatorial 𝛽-plane. J. Atmos. Sci. 50, 2744–2758.Google Scholar
Eliassen, A. 1951 Slow thermally or frictionally controlled meridional circulation in a circular vortex. Astrophysica Norvegia 5, 19–60.Google Scholar
Ertel, H. 1942a Ein neuer hydrodynamischer Wirbelsazt. Meteorol. Z. 59, 271–281.Google Scholar
Ertel, H. 1942b Uber des Verhältnis das neuen hydrodynamischen Wirbelsatzes zum Zirkulationssatz von V. Bjerknes. Meteorol. Z. 59, 385–387.Google Scholar
Firing, E. 1987 Deep zonal currents in the central equatorial Pacific. J. Mar. Res. 45, 791–812.Google Scholar
Fjørtoft, R. 1950 Application of integral theorems in deriving criteria of stability for laminar flows and for the baroclinic circular vortex. Geofys. Publ. 17, 1–52.Google Scholar
Fruman, M. D. & Shepherd, T. G. 2008 Symmetric stability of compressible zonal flows on a generalized equatorial 𝛽 plane. J. Atmos. Sci. 65, 1927–1940.CrossRefGoogle Scholar
Gerkema, T., Zimmerman, J. T. F., Maas, L. R. M. & van Haren, H. N. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46, 1–33.Google Scholar
Gill, A. E. 1982 Atmosphere–Ocean Dynamics. Academic.Google Scholar
Griffiths, S. D. 2003a The nonlinear evolution of zonally symmetric equatorial inertial instability. J. Fluid Mech. 474, 245–273.Google Scholar
Griffiths, S. D. 2003b Nonlinear vertical scale selection in equatorial inertial instability. J. Atmos. Sci. 60, 977–990.Google Scholar
Griffiths, S. D. 2008a The limiting form of inertial instability in geophysical flows. J. Fluid Mech. 605, 115–143.Google Scholar
Griffiths, S. D. 2008b Weakly diffusive vertical scale selection for the inertial instability of an arbitrary shear flow. J. Fluid Mech. 594, 265–268.Google Scholar
Grimshaw, R. H. J. 1975 A note on the 𝛽-plane approximation. Tellus A 27, 351–357.Google Scholar
Høiland, E. 1962 Discussion of a hyperbolic equation relating to inertia and gravitational fluid oscillations. Geofys. Publ. 24, 211–227.Google Scholar
Holton, J. R. 1992 An Introduction to Dynamic Meteorology, 3rd edn. Academic.Google Scholar
Hoskins, B. J. 1974 The role of potential vorticity in symmetric stability and instability. Q. J. R. Meteorol. Soc. 100, 480–482.Google Scholar
Hua, B. L., Moore, D. W. & Le Gentil, S. 1997 Inertial nonlinear equilibration of equatorial flows. J. Fluid Mech. 331, 345–371.Google Scholar
Kloosterziel, R. C. & Carnevale, G. F. 2007 Generalized energetics for inertially stable parallel shear flows. J. Fluid Mech. 585, 117–126.Google Scholar
Kloosterziel, R. C. & Carnevale, G. F. 2008 Vertical scale selection in inertial instability. J. Fluid Mech. 594, 249–269.Google Scholar
Kloosterziel, R. C., Carnevale, G. F. & Orlandi, P. 2007a Inertial instability in rotating and stratified fluids: barotropic vortices. J. Fluid Mech. 583, 379–412.CrossRefGoogle Scholar
Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2007b Saturation of inertial instability in rotating planar shear flows. J. Fluid Mech. 583, 413–422.CrossRefGoogle Scholar
Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2015 Saturation of equatorial inertial instability. J. Fluid Mech. 767, 562–594.Google Scholar
LeBlond, P. H. & Mysak, L. A. 1978 Waves in the Ocean. Elsevier.Google Scholar
Lukas, R. & Lindstrom, E. 1991 The mixed layer of the western equatorial Pacific Ocean. J. Geophys. Res. 96, 3343–3357.CrossRefGoogle Scholar
Luyten, J. R. & Swallow, J. C. 1976 Equatorial undercurrents. Deep Sea Res. 23, 999–1001.Google Scholar
Natarov, A. & Richards, K. J. 2009 Three-dimensional instabilities of oscillatory equatorial zonal shear flows. J. Fluid Mech. 623, 59–74.Google Scholar
Ooyama, K. 1966 On the stability of the baroclinic circular vortex: a sufficient condition for instability. J. Atmos. Sci. 23, 43–53.2.0.CO;2>CrossRefGoogle Scholar
Orlandi, P. 2000 Fluid Flow Phenomena: A Numerical Toolkit. Kluwer.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Phillips, N. A. 1966 The equations of motion for a shallow rotating atmosphere and the traditional approximation. J. Atmos. Sci. 23, 626–628.Google Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21, 106601.Google Scholar
Rayleigh, Lord 1916 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Ribstein, B., Plougonven, R. & Zeitlin, V. 2014 Inertial versus baroclinic instability of the Bickley jet in a continuously stratified rotating fluid. J. Fluid Mech. 743, 1–31.Google Scholar
Sawyer, J. S. 1949 The significance of dynamic instability in atmospheric motions. Q. J. R. Meteorol. Soc. 75, 364–374.Google Scholar
Sipp, D. & Jacquin, L. 2000 Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 12 (7), 1740–1748.Google Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11, 305–322.Google Scholar
Solberg, H. 1936 Le mouvement d’inertie de l’atmosphère stable et son rôle dans la théorie des cyclones. In Sixth Assembly, Edinburgh, pp. 66–82. Union Géodésique et Géophysique Internationale.Google Scholar
Tort, M., Dubos, T., Bouchut, F. & Zeitlin, V. 2014 Consistent shallow-water equations on the rotating sphere with complete Coriolis force and topography. J. Fluid Mech. 748, 289–821.Google Scholar
Tort, M., Ribstein, B. & Zeitlin, V. 2016 Symmetric and asymmetric inertial instability of zonal jets on the f-plane with complete Coriolis force. J. Fluid Mech. 788, 274–301.CrossRefGoogle Scholar
Veronis, G. 1963 On the approximations involved in transforming the equations of motion from a spherical surface to the 𝛽-plane: barotropic systems. J. Mar. Res. 21 (2), 110–124.Google Scholar
Yanai, M. & Tokiaka, T. 1969 Axially symmetric meridional motions in the baroclinic circular vortex: a numerical experiment. J. Met. Soc. Japan 47 (3), 183–197.Google Scholar