Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T13:21:45.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Entrainment and mixed layer dynamics of a surface-stress-driven stratified fluid

Published online by Cambridge University Press:  28 January 2015

G. E. Manucharyan  and
C. P. Caulfield
G. E. Manucharyan*
Affiliation:
Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider experimentally an initially quiescent and linearly stratified fluid with buoyancy frequency 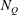$N_{Q}$ in a cylinder subject to surface-stress forcing from a disc of radius 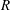$R$ spinning at a constant angular velocity 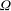${\rm\Omega}$. We observe the growth of the disc-adjacent turbulent mixed layer bounded by a sharp primary interface with a constant characteristic thickness 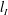$l_{I}$. To a good approximation the depth of the forced mixed layer scales as 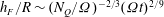$h_{F}/R\sim (N_{Q}/{\rm\Omega})^{-2/3}({\rm\Omega}t)^{2/9}$. Generalising the previous arguments and observations of Shravat et al. (J. Fluid Mech., vol. 691, 2012, pp. 498–517), we show that such a deepening rate is consistent with three central assumptions that allow us to develop a phenomenological energy balance model for the entrainment dynamics. First, the total kinetic energy of the deepening mixed layer 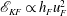$\mathscr{E}_{KF}\propto h_{F}u_{F}^{2}$, where 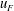$u_{F}$ is a characteristic velocity scale of the turbulent motions within the forced layer, is essentially independent of time and the buoyancy frequency 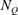$N_{Q}$. Second, the scaled entrainment parameter 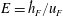$E={\dot{h}}_{F}/u_{F}$ depends only on the local interfacial Richardson number 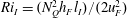$Ri_{I}=(N_{Q}^{2}h_{F}l_{I})/(2u_{F}^{2})$. Third, the potential energy increase (due to entrainment, mixing and homogenisation throughout the deepening mixed layer) is driven by the local energy input at the interface, and hence is proportional to the third power of the characteristic velocity 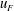$u_{F}$. We establish that internal consistency between these assumptions implies that the rate of increase of the potential energy (and hence the local mass flux across the primary interface) decreases with 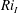$Ri_{I}$. This observation suggests, as originally argued by Phillips (Deep-Sea Res., vol. 19, 1972, pp. 79–81), that the mixing in the vicinity of the primary interface leads to the spontaneous appearance of secondary partially mixed layers, and we observe experimentally such secondary layers below the primary interface.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 653 - 667
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J., Llewellyn Smith, S. G. & Young, W. R. 1998 Dynamics of interfaces and layers in a stratified turbulent fluid. J. Fluid Mech. 355, 329–358.Google Scholar
Boyer, D. L., Davies, P. A. & Guo, Y. 1997 Mixing of a two-layer stratified fluid by a rotating disc. Fluid Dyn. Res. 21, 381–401.Google Scholar
Davies, P. A., Guo, Y., Boyer, D. L. & Folkard, A. M. 1995 The flow generated by the rotation of a horizontal disc in a stratified fluid. Fluid Dyn. Res. 17, 27–47.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23, 455–493.Google Scholar
Ferrari, R. & Wunsch, C. 2009 Ocean circulation kinetic energy: reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 41, 253–282.Google Scholar
Holford, J. M. & Linden, P. F. 1999 Turbulent mixing in a stratified fluid. Dyn. Atmos. Ocean. 30, 173–198.CrossRefGoogle Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.CrossRefGoogle Scholar
Kato, H. & Phillips, O. M. 1969 On the penetration of a turbulent layer into stratified fluid. J. Fluid Mech. 37, 643–655.Google Scholar
Kit, E., Berent, E. & Vajda, M. 1980 Vertical mixing induced by wind and a rotating screen in a stratified fluid in a channel. J. Hydraul. Res. 18, 35–57.CrossRefGoogle Scholar
Large, W. G., McWilliams, J. C. & Doney, S. C. 1994 Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–403.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13, 3–23.Google Scholar
Munro, R. J. & Davies, P. A. 2006 The flow generated in a continuously stratified rotating fluid by the differential rotation of a plane horizontal disc. Fluid Dyn. Res. 38, 522–538.Google Scholar
Munro, R. J., Foster, M. R. & Davies, P. A. 2010 Instabilities in the spin-up of a rotating, stratified fluid. Phys. Fluids 22, 054108.Google Scholar
Oglethorpe, R. L. F., Caulfield, C. P. & Woods, A. W. 2013 Spontaneous layering in stratified turbulent Taylor–Couette flow. J. Fluid Mech. 721, R3.Google Scholar
Park, Y.-G., Whitehead, J. A. & Gnanadeskian, A. 1994 Turbulent mixing in stratified fluids: layer formation and energetics. J. Fluid Mech. 279, 279–311.CrossRefGoogle Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid – is it unstable? Deep-Sea Res. 19, 79–81.Google Scholar
Shravat, A., Cenedese, C. & Caulfield, C. P. 2012 Entrainment and mixing dynamics of surface-stress-driven stratified flow in a cylinder. J. Fluid Mech. 691, 498–517. Referred to herein as SCC12.Google Scholar
Turner, J. S. 1968 The influence of molecular diffusivity on turbulent entrainment across a density interface. J. Fluid Mech. 33, 639–656.Google Scholar
Woods, A. W., Caulfield, C. P., Landel, J. R. & Kuesters, A. 2010 Non-invasive turbulent mixing across a density interface in a turbulent Taylor–Couette flow. J. Fluid Mech. 663, 347–357.CrossRefGoogle Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.CrossRefGoogle Scholar