Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-03T01:00:03.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Entrainment across a sheared density interface in a cavity flow

Published online by Cambridge University Press:  29 November 2017

N. Williamson Open the ORCID record for N. Williamson [Opens in a new window] ,
M. P. Kirkpatrick  and
S. W. Armfield
N. Williamson*
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, New South Wales 2006, Australia
M. P. Kirkpatrick
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, New South Wales 2006, Australia
S. W. Armfield
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, New South Wales 2006, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The entrainment of fluid across a sheared density interface has been examined experimentally in a purging cavity flow. In this flow, a long straight cavity with sloped entry and exit boundaries is located in the base of a straight open channel. Dense cavity fluid is entrained from the cavity into the turbulent overflow. The cavity geometry has been designed to ensure there is no separation of the overflow in the cavity region, with the goal of avoiding cavity-specific entrainment mechanisms as have been encountered in most previous experiments using similar arrangements. Results are obtained over a bulk Richardson number range 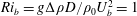$Ri_{b}=g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}D/\unicode[STIX]{x1D70C}_{0}U_{b}^{2}=1$ to 19, where 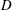$D$ and 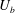$U_{b}$ are the depth of the mixed layer and bulk velocity in the cavity, respectively. The experiments cover the Reynolds number range 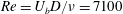$Re=U_{b}D/\unicode[STIX]{x1D708}=7100$ to 15 100 and interface length to mixed layer depth ratios of 2.4 to 16. Particle image velocimetry and laser induced fluorescence measurements indicate the flow regime over this entire range is one dominated by the Holmboe wave instability. The non-dimensional entrainment rate, 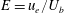$E=u_{e}/U_{b}$, is shown to scale with the bulk Richardson number. We find that the entrainment scaling 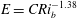$E=CRi_{b}^{-1.38}$ applies over the entire experimental range, with no apparent dependence on interface length. The exponent in the scaling is similar to previous non-cavity-based sheared interface flows, however, the constant 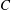$C$ is up to an order of magnitude smaller. Close agreement is, however, obtained by instead correlating entrainment with the local gradient Richardson number centred on the interface, rather than bulk quantities. We obtain 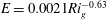$E=0.0021Ri_{g}^{-0.63}$ for data over 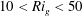$10<Ri_{g}<50$, where 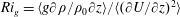$Ri_{g}=\langle g\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x2202}z\rangle /\langle (\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}z)^{2}\rangle$. The density interface is much thinner and therefore more stable in the present flow configuration compared with other published results for the same bulk Richardson number. We suggest that our configuration ensures a sharp mixing layer profile at the upstream end of the cavity even at relatively low bulk Richardson numbers of 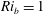$Ri_{b}=1$ and that the reduced mixing in the Holmboe wave regime allows the interface to retain its sharp character over the cavity length, resulting in weak sensitivity to cavity length.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 999 - 1021
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, G. 1988 Turbulence and Mixing in Stratified Tidal Flows, pp. 149–180. Springer.Google Scholar
Baratian-Ghorghi, Z. & Kaye, N. B. 2013 Modeling the purging of dense fluid from a street canyon driven by an interfacial mixing flow and skimming flow. Phys. Fluids 25 (7), 076603.CrossRefGoogle Scholar
Browand, F. K. & Winant, C. D. 1973 Laboratory observations of shear-layer instability in a stratified fluid. Boundary-Layer Meteorol. 5 (1–2), 67–77.CrossRefGoogle Scholar
Carpenter, J. R., Lawrence, G. A. & Smyth, W. D. 2007 Evolution and mixing of asymmetric Holmboe instabilities. J. Fluid Mech. 582, 103–132.CrossRefGoogle Scholar
Carpenter, J. R., Tedford, E. W., Rahmani, M. & Lawrence, G. A. 2010 Holmboe wave fields in simulation and experiment. J. Fluid Mech. 648, 205–223.CrossRefGoogle Scholar
Chang, K., Constantinescu, G. & Park, S.-O. 2006 Analysis of the flow and mass transfer processes for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer. J. Fluid Mech. 561, 113–145.CrossRefGoogle Scholar
Christodoulou, G. C. 1986 Interfacial mixing in stratified flows. J. Hydraul. Res. 24 (2), 77–92.Google Scholar
Chu, V. H. & Baddour, R. E. 1984 Turbulent gravity-stratified shear flows. J. Fluid Mech. 138, 353–378.Google Scholar
Deardorff, J. W. & Willis, G. E. 1982 Dependence of mixed-layer entrainment on shear stress and velocity jump. J. Fluid Mech. 115, 123–149.CrossRefGoogle Scholar
Deardorff, J. W. & Yoon, S.-C. 1984 On the use of an annulus to study mixed-layer entrainment. J. Fluid Mech. 142, 97–120.Google Scholar
Debler, W. & Armfield, S. W. 1997 The purging of saline water from rectangular and trapezoidal cavities by an overflow of turbulent sweet water. J. Hydraul. Res. 35 (1), 43–62.Google Scholar
Debler, W. & Imberger, J. 1996 Flushing criteria in estuarine and laboratory experiments. J. Hydraul. Engng 122 (12), 728–734.Google Scholar
Fernando, H. J. S., Zajic, D., Di Sabatino, S., Dimitrova, R., Hedquist, B. & Dallman, A. 2010 Flow, turbulence, and pollutant dispersion in urban atmospheres. Phys. Fluids 22 (5), 051301.Google Scholar
Gillam, N. L., Armfield, S. W. & Kirkpatrick, M. P. 2009 Influence of a channel bend on the purging of saline fluid from a cavity by an overflow of fresh water. ANZIAM J. 50, C990–C1003.Google Scholar
Hewitt, G. F.1960 Tables of the resistivity of aqueous sodium chloride solutions. Tech. Rep. AERE-R-3497. United Kingdom Atomic Energy Authority Research Group, Atomic Energy Research Establishment, Harwell, Berks, England.Google Scholar
Hogg, A. M. & Ivey, G. N. 2003 The Kelvin–Helmholtz to Holmboe instability transition in stratified exchange flows. J. Fluid Mech. 477, 339–362.Google Scholar
Holmboe, J. 1962 On the behavior of symmetric waves in stratified shear layers. Geophys. Publ. 24, 67–113.Google Scholar
Kantha, L. H., Phillips, O. M. & Azad, R. S. 1977 On turbulent entrainment at a stable density interface. J. Fluid Mech. 79 (4), 753–768.CrossRefGoogle Scholar
Kato, H. & Phillips, O. M. 1969 On the penetration of a turbulent layer into stratified fluid. J. Fluid Mech. 37 (4), 643–655.CrossRefGoogle Scholar
Kirkpatrick, M. P. & Armfield, S. W. 2005 Experimental and large eddy simulation results for the purging of salt water from a cavity by an overflow of fresh water. Intl J. Heat Mass Transfer 48 (2), 341–359.CrossRefGoogle Scholar
Kirkpatrick, M. P., Armfield, S. W. & Williamson, N. 2012 Shear driven purging of negatively buoyant fluid from trapezoidal depressions and cavities. Phys. Fluids 24 (2), 025106.Google Scholar
Lofquist, K. 1960 Flow and stress near an interface between stratified liquids. Phys. Fluids 3 (2), 158–175.Google Scholar
Narimousa, S. & Fernando, H. J. S. 1987 On the sheared density interface of an entraining stratified fluid. J. Fluid Mech. 174, 1–22.Google Scholar
Narimousa, S., Long, R. R. & Kitaigorodskii, S. A. 1986 Entrainment due to turbulent shear flow at the interface of a stably stratified fluid. Tellus A 38A (1), 76–87.Google Scholar
Price, J. F. 1979 On the scaling of stress-driven entrainment experiments. J. Fluid Mech. 90 (3), 509–529.CrossRefGoogle Scholar
Salehipour, H., Caulfield, C. P. & Peltier, W. R. 2016 Turbulent mixing due to the Holmboe wave instability at high Reynolds number. J. Fluid Mech. 803, 591–621.Google Scholar
Scranton, D. R. & Lindberg, W. R. 1983 An experimental study of entraining, stress-driven, stratified flow in an annulus. Phys. Fluids 26 (5), 1198–1205.CrossRefGoogle Scholar
Smyth, W. D., Carpenter, J. R. & Lawrence, G. A. 2007 Mixing in symmetric Holmboe waves. J. Phys. Oceanogr. 37 (6), 1566–1583.Google Scholar
Smyth, W. D., Klaassen, G. P. & Peltier, W. R. 1988 Finite amplitude Holmboe waves. Geophys. Astrophys. Fluid Dyn. 43 (2), 181–222.Google Scholar
Smyth, W. D. & Winters, K. B. 2003 Turbulence and mixing in Holmboe waves. J. Phys. Oceanogr. 33 (4), 694–711.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2004 Shear-induced mixing and transport from a rectangular cavity. J. Fluid Mech. 520, 23–49.Google Scholar
Sullivan, G. D. & List, E. J. 1994 On mixing and transport at a sheared density interface. J. Fluid Mech. 273, 213–239.Google Scholar
Tedford, E. W., Pieters, R. & Lawrence, G. A. 2009 Symmetric Holmboe instabilities in a laboratory exchange flow. J. Fluid Mech. 636, 137–153.CrossRefGoogle Scholar
Xuequan, E. & Hopfinger, E. J. 1986 On mixing across an interface in stably stratified fluid. J. Fluid Mech. 166, 227–244.Google Scholar

Williamson et al. supplementary movie

Laser induced fluorescence image sequence for flow at Ri_b=4.1, Ri_g=27 and Re=7100. The images are presented in false colour, which indicates fluid density. Flow is from right to left.

Download Williamson et al. supplementary movie(Video)
Video 12.1 MB