Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-19T16:13:16.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy spectra power laws and structures

Published online by Cambridge University Press:  06 March 2009

P. ORLANDI
P. ORLANDI*
Affiliation:
Dipartimento di Meccanica e Aeronautica, Università La Sapienza, Via Eudosiana 16, I-00184, Roma
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of two inviscid flows, the Taylor–Green flow and two orthogonal interacting Lamb dipoles, together with the DNS of forced isotropic turbulence, were performed to generate data for a comparative study. The isotropic turbulent field was considered after the transient and, in particular, when the velocity derivative skewness oscillates around −0.5. At this time, Rλ ≈ 257 and a one decade wide k−5/3 range was present in the energy spectrum. For the inviscid flows the fields were considered when a wide k−3 range was achieved. This power law spectral decay corresponds to infinite enstrophy and is considered one of the requirements to demonstrate that the Euler equations lead to a finite time singularity (FTS). 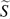Flow visualizations and statistics of the strain rate tensor and vorticity components in the principal axes of the strain rate tensor (λ, 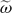λ) were used to classify structures. The key role of the intermediate component 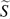2 is demonstrated by its good correlation with enstrophy production. Filtering of the fields shows that the slope of the power law is directly connected to self-similar structures, whose radius of curvature is smaller the steeper the spectrum.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 623 , 25 March 2009 , pp. 353 - 374
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alvelius, K. 1999 Random forcing of three-dimensional homogeneous turbulence. Phys. Fluids 11, 1880–1889.CrossRefGoogle Scholar
Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.CrossRefGoogle Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005 Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101.CrossRefGoogle Scholar
Cichowlas, C. & Brachet, M. 2005 Evolution of complex singularities in KidaPelz and Taylor—Green inviscid flows. Fluid Dyn. Res. 36, 239–248.CrossRefGoogle Scholar
Cichowlas, C., Debbashn, F. & Brachet, M. 2006 Evolution of complex singularities and Kolmogorov scaling in truncated three-dimensional Euler flows. In IUTAM Symposium on Elementary Vortices and Coherent Structures: Significance in Turbulence Dynamics, pp. 319–328. Springer.CrossRefGoogle Scholar
Crocco, L. & Orlandi, P. 1985 A transformation for the energy-transfer term in isotropic turbulence. J. Fluid Mech. 161, 405–424.CrossRefGoogle Scholar
Domaradzki, J. & Rogallo, R. S. 1990 Local energy transfer and nonlocal interactions in homogeneous, isotropic turbulence. Phys. Fluids A 2, 413–426.CrossRefGoogle Scholar
Duponcheel, M., Orlandi, P. & Winckelmans, G. 2008 Time-reversibility of the Euler equations as a benchmark for energy conserving schemes. J. Comput. Phys. 227, 8736–8752.CrossRefGoogle Scholar
Gotoh, T. Fukayama, D., & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14 (3), 1065–1081.CrossRefGoogle Scholar
Grafke, T., Homan, H., Dreher, J. & Grauer, R. 2007 Numerical simulations of possible finite time singularities in the incompressible Euler equations: comparison of numerical methods. ArXiv:0711.2284v1 physics.flu-dyn.Google Scholar
Holm, D. D. & Kerr, R. M. 2007 Helicity in the formation of turbulence. Phys. Fluids 19, 025101.CrossRefGoogle Scholar
Horiuti, K. & Fujisawa, Y. 2008 The multi-mode stretched spiral vortex in homogeneous isotropic turbulence. J. Fluid Mech. 595, 341–366.CrossRefGoogle Scholar
Horiuti, K. & Takagi, Y. 2005 Identification method for vortex sheet structures in turbulent flows. Phys. Fluids 17, 121703.CrossRefGoogle Scholar
Hou, T. Y. & Li, R. 2006 Dynamic depletion of vortex stretching and non-blowup of the 3-D incompressible Euler equations. J. Nonlinear Sci. 16, 639–664.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2005 Energy spectrum in the near dissipation range of high resolution direct numerical simulation of turbulence. J. Phys. Soc. Jpn 74, 1464–1471.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Kaneda, Y. Ishihara, T., Yokokawa, M. Itakura, K. & Uno, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box. Phys. Fluids 15, L21.CrossRefGoogle Scholar
Kerr, R. M. 1987 Histograms of helicity and strain in numerical turbulence. Phys. Rev. Lett. 59, 783–786.CrossRefGoogle ScholarPubMed
Kerr, R. M. 1993 Evidence for a singularity of the three-dimensional, incompressible Euler equations. Phys. Fluids A 5, 1725–1746.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 [1991] The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl Akad. Nauk SSSR 30, 301–305. English translation in Proc. R. Soc. Lond. A 434, 9–13.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Moisy, F., & Jimenez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.CrossRefGoogle Scholar
Orlandi, P. 2000. Fluid Flow Phenomena: A Numerical Toolkit. Kluwer Academic Publishers.CrossRefGoogle Scholar
Orlandi, P., & Carnevale, G. F. 2007 Nonlinear amplification of vorticity in inviscid interaction of orthogonal Lamb dipoles. Phys. Fluids 19 (5), 057106.CrossRefGoogle Scholar
Paczuski, M. & Bak, P. 1999 Self-organization of complex systems. ArXiv: cond-mat/9906077.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
She, Z. S., Jackson, E. & Orszag, S. A. 1991 Structure and dynamics of homogeneous turbulence:models and simulations. Proc. R. Soc. Lond. A 434, 101–124.Google Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.CrossRefGoogle Scholar