Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T09:16:41.045Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy spectra in turbulent bubbly flows

Published online by Cambridge University Press:  15 February 2016

Vivek N. Prakash ,
J. Martínez Mercado ,
Leen van Wijngaarden ,
E. Mancilla ,
Y. Tagawa ,
Detlef Lohse  and
Chao Sun
Vivek N. Prakash
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Department of Bioengineering, Stanford University, Stanford, CA 94305, USA
J. Martínez Mercado
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Leen van Wijngaarden
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
E. Mancilla
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Instituto de Investigaciones en Materiales, Universidad Nacional Autónoma de México, México Distrito Federal 04510, México
Y. Tagawa
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Department of Mechanical Systems Engineering, Tokyo University of Agriculture and Technology, 1848588, Koganei-city, Tokyo, Japan
Detlef Lohse
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Max Planck Institute for Dynamics and Self-Organization, D-37077 Göttingen, Germany
Chao Sun*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Center for Combustion Energy and Department of Thermal Engineering, Tsinghua University, Beijing 100084, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

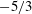We conduct experiments in a turbulent bubbly flow to study the nature of the transition between the classical $-5/3$ energy spectrum scaling for a single-phase turbulent flow and the 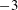$-3$ scaling for a swarm of bubbles rising in a quiescent liquid and of bubble-dominated turbulence. The bubblance parameter (Lance & Bataille J. Fluid Mech., vol. 222, 1991, pp. 95–118; Rensen et al., J. Fluid Mech., vol. 538, 2005, pp. 153–187), which measures the ratio of the bubble-induced kinetic energy to the kinetic energy induced by the turbulent liquid fluctuations before bubble injection, is often used to characterise bubbly flow. We vary the bubblance parameter from 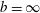$b=\infty$ (pseudoturbulence) to 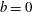$b=0$ (single-phase flow) over 2–3 orders of magnitude (0.01–5) to study its effect on the turbulent energy spectrum and fluctuations in liquid velocity. The probability density functions (PDFs) of the fluctuations in liquid velocity show deviations from the Gaussian profile for 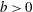$b>0$, i.e. when bubbles are present in the system. The PDFs are asymmetric with higher probability in the positive tails. The energy spectra are found to follow the 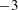$-3$ scaling at length scales smaller than the size of the bubbles for bubbly flows. This 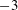$-3$ spectrum scaling holds not only in the well-established case of pseudoturbulence, but surprisingly in all cases where bubbles are present in the system (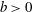$b>0$). Therefore, it is a generic feature of turbulent bubbly flows, and the bubblance parameter is probably not a suitable parameter to characterise the energy spectrum in bubbly turbulent flows. The physical reason is that the energy input by the bubbles passes over only to higher wavenumbers, and the energy production due to the bubbles can be directly balanced by the viscous dissipation in the bubble wakes as suggested by Lance & Bataille (1991). In addition, we provide an alternative explanation by balancing the energy production of the bubbles with viscous dissipation in the Fourier space.

JFM classification

Multiphase and Particle-laden Flows: Gas/liquid flow Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 174 - 190
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van den Berg, T. H., Wormgoor, W. D., Luther, S. & Lohse, D. 2011 Phase-sensitive constant temperature anemometry. Macromol. Mater. Engng 296, 230–237.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
Cui, Z. & Fan, L. S. 2004 Turbulence energy distributions in bubbling gas–liquid and gas–liquid–solid flow systems. Chem. Engng Sci. 59, 1755–1766.CrossRefGoogle Scholar
Deckwer, B. D. 1992 Bubble Column Reactors, 1st edn. Wiley.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of freely rising or falling bodies. Annu. Rev. Fluid Mech. 44, 97–121.Google Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly water–air flow. J. Fluid Mech. 222, 95–118.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.Google Scholar
Martinez Mercado, J., Chehata, D., van Gils, D. P. M., Sun, C. & Lohse, D. 2010 On bubble clustering and energy spectra in pseudo-turbulence. J. Fluid Mech. 650, 287–306.CrossRefGoogle Scholar
Martinez Mercado, J., Palacios Morales, C. & Zenit, R. 2007 Measurements of pseudoturbulence intensity in monodispersed bubbly liquids for $10<Re<500$ . Phys. Fluids 19, 103302.Google Scholar
Martinez Mercado, J., Prakash, V. N., Tagawa, Y., Sun, C. & Lohse, D. 2012 Lagrangian statistics of light particles in turbulence. Phys. Fluids 24, 055106.Google Scholar
Mazzitelli, I. & Lohse, D. 2009 Evolution of energy in flow driven by rising bubbles. Phys. Rev. E 79, 066317.Google Scholar
Mendez-Diaz, S., Serrano-Garcia, J. C., Zenit, R. & Hernandez-Cordero, J. A. 2013 Power spectral distributions of pseudo-turbulent bubbly flows. Phys. Fluids 25, 043303.Google Scholar
Mudde, R. F., Groen, J. S. & van der Akker, H. E. A. 1997 Liquid velocity field in a bubble column: LDA experiments. Chem. Engng Sci. 52, 4217–4224.Google Scholar
Poorte, R. E. G. & Biesheuvel, A. 2002 Experiments on the motion of gas bubbles in turbulence generated by an active grid. J. Fluid Mech. 461, 127–154.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prakash, V. N., Tagawa, Y., Calzavarini, E., Martinez Mercado, J., Toschi, F., Lohse, D. & Sun, C. 2012 How gravity and size affect the acceleration statistics of bubbles in turbulence. New J. Phys. 14, 105017.Google Scholar
Rensen, J., Luther, S. & Lohse, D. 2005 The effects of bubbles on developed turbulence. J. Fluid Mech. 538, 153–187.Google Scholar
Riboux, G., Legendre, D. & Risso, F. 2013 A model of bubble-induced turbulence based on large-scale wake interactions. J. Fluid Mech. 719, 362–387.Google Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.Google Scholar
Risso, F. 2011 Theoretical model for $k^{-3}$ spectra in dispersed multiphase flows. Phys. Fluids 23, 011701.Google Scholar
Risso, F. & Ellingsen, K. 2002 Velocity fluctuations in a homogeneous dilute dispersion of high-Reynolds-number rising bubbles. J. Fluid Mech. 453, 395–410.Google Scholar
Risso, F., Roig, V., Amoura, Z., Riboux, G. & Billet, A. M. 2008 Wake attenuation in large Reynolds number dispersed two-phase flows. Phil. Trans. R. Soc. Lond. A 366, 2177–2190.Google ScholarPubMed
Roghair, I., Martínez Mercado, J., Van Sint Annaland, M., Kuipers, J. A. M., Sun, C. & Lohse, D. 2011 Energy spectra and bubble velocity distributions in pseudo-turbulence: numerical simulations versus experiments. Intl J. Multiphase Flow 37, 1–6.Google Scholar
Zenit, R., Koch, D. L. & Sangani, A. S. 2001 Measurements of the average properties of a suspension of bubbles rising in a vertical channel. J. Fluid Mech. 429, 307–342.Google Scholar