Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T08:01:08.045Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy exchanges in the flow past a cylinder with a leeward control rod

Published online by Cambridge University Press:  03 May 2022

Neelakash Biswas Open the ORCID record for Neelakash Biswas [Opens in a new window] ,
Murilo M. Cicolin Open the ORCID record for Murilo M. Cicolin [Opens in a new window]  and
Oliver R.H. Buxton Open the ORCID record for Oliver R.H. Buxton [Opens in a new window]
Neelakash Biswas*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
Murilo M. Cicolin
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK Escola Politécnica, University of São Paulo, Brazil
Oliver R.H. Buxton
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the energy exchanges between coherent structures and the mean flow in the wake of a cylinder in the presence of a leeward control rod using particle image velocimetry data at Reynolds number ($Re$) $20\times 10^3$. The shedding of the control rod depends on the oncoming shear layer and hence the downstream interaction of the main cylinder's and control rod's wake strongly depends on the control rod's setting angle ($\theta$). 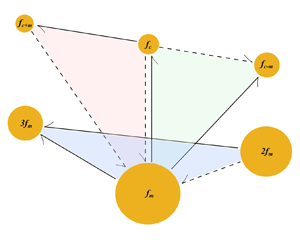In this work we study this interaction between the shedding modes from the cylinder and control rod at different $\theta$. New secondary coherent motions with distinct characteristic frequencies appear in the flow field aside from the frequencies associated with the sheddings of the control rod, the main cylinder and its harmonics. A multiscale triple decomposition method is applied to extract the coherent modes associated with each of these frequencies, and the dynamics of the modes are studied using kinetic energy budget equations. The primary shedding modes of the control rod and main cylinder, as well as the harmonics of the main cylinder's shedding modes, are found to be primarily energised by the mean flow at this $Re$, while the secondary modes are almost entirely energised by the primary modes, similar to the findings of Baj & Buxton (Phys. Rev. Fluids, vol. 2, issue 11, 2017, 114607) for a different multiscale flow configuration. The remarkable similarity in the energy exchange process forming the secondary coherent modes, observed in two different studies, hints at a possible universality in the formation process of these secondary structures in a multiscale flow.

JFM classification

Wakes/Jets: Wakes Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 941 , 25 June 2022 , A36
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alam, M.M., Moriya, M. & Sakamoto, H. 2003 Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. J. Fluids Struct. 18 (3–4), 325–346.CrossRefGoogle Scholar
Baj, P., Bruce, P.J. & Buxton, O.R. 2015 The triple decomposition of a fluctuating velocity field in a multiscale flow. Phys. Fluids 27 (7), 075104.CrossRefGoogle Scholar
Baj, P. & Buxton, O.R. 2017 Interscale energy transfer in the merger of wakes of a multiscale array of rectangular cylinders. Phys. Rev. Fluids 2 (11), 114607.CrossRefGoogle Scholar
Baj, P. & Buxton, O.R. 2019 Passive scalar dispersion in the near wake of a multi-scale array of rectangular cylinders. J. Fluid Mech. 864, 181–220.CrossRefGoogle Scholar
Bearman, P. & Wadcock, A. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61 (3), 499–511.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108 (16), 164501.CrossRefGoogle ScholarPubMed
Bingham, C., Morton, C. & Martinuzzi, R.J. 2018 Influence of control cylinder placement on vortex shedding from a circular cylinder. Exp. Fluids 59 (10), 158.CrossRefGoogle Scholar
Browne, L., Antonia, R. & Shah, D. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307–326.CrossRefGoogle Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
Cicolin, M., Buxton, O., Assi, G. & Bearman, P. 2021 The role of separation on the forces acting on a circular cylinder with a control rod. J. Fluid Mech. 915, A33.CrossRefGoogle Scholar
Dalton, C., Xu, Y. & Owen, J. 2001 The suppression of lift on a circular cylinder due to vortex shedding at moderate Reynolds numbers. J. Fluids Struct. 15 (3–4), 617–628.CrossRefGoogle Scholar
Dipankar, A., Sengupta, T. & Talla, S. 2007 Suppression of vortex shedding behind a circular cylinder by another control cylinder at low Reynolds numbers. J. Fluid Mech. 573, 171–190.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. 2012 Particle image velocimetry study of fractal-generated turbulence. J. Fluid Mech. 711, 306–336.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. 2015 The energy cascade in near-field non-homogeneous non-isotropic turbulence. J. Fluid Mech. 771, 676–705.CrossRefGoogle Scholar
Hinze, J. 1975 Turbulence, McGraw-Hill classic textbook reissue series. McGraw-Hill. ISBN 9780070290372.Google Scholar
Hussain, A.F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Hussain, A.K.M.F. & Reynolds, W.C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41 (2), 241–258.CrossRefGoogle Scholar
Jin, B., Symon, S. & Illingworth, S.J. 2021 Energy transfer mechanisms and resolvent analysis in the cylinder wake. Phys. Rev. Fluids 6 (2), 024702.CrossRefGoogle Scholar
Laizet, S. & Vassilicos, J. 2012 Fractal space-scale unfolding mechanism for energy-efficient turbulent mixing. Phys. Rev. E 86 (4), 046302.CrossRefGoogle ScholarPubMed
Lam, K.M., Wong, P. & Ko, N.W.M. 1993 Interaction of flows behind two circular cylinders of different diameters in side-by-side arrangement. Expl Therm. Fluid Sci. 7 (3), 189–201.CrossRefGoogle Scholar
Lekoudis, S. & Sengupta, T. 1986 Two-dimensional turbulent boundary layers over rigid and moving swept wavy surfaces. Phys. Fluids 29 (4), 964–970.CrossRefGoogle Scholar
Liu, X. & Thomas, F.O. 2004 Measurement of the turbulent kinetic energy budget of a planar wake flow in pressure gradients. Exp. Fluids 37, 469–482.CrossRefGoogle Scholar
Mazellier, N. & Vassilicos, J. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22 (7), 075101.CrossRefGoogle Scholar
Mittal, S. & Raghuvanshi, A. 2001 Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Intl J. Numer. Meth. Fluids 35 (4), 421–447.3.0.CO;2-M>CrossRefGoogle Scholar
Monkewitz, P. & Nguyen, L. 1987 Absolute instability in the near-wake of two-dimensional bluff bodies. J. Fluids Struct. 1 (2), 165–184.CrossRefGoogle Scholar
Morris, E.M., Biswas, N., Aleyasin, S.S. & Tachie, M.F. 2021 Particle image velocimetry measurements of turbulent jets issuing from twin elliptic nozzles with various orientations. Trans. ASME J. Fluids Engng 143 (2), 021501.CrossRefGoogle Scholar
Panchapakesan, N.R. & Lumley, J.L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.CrossRefGoogle Scholar
Parezanović, V. & Cadot, O. 2012 Experimental sensitivity analysis of the global properties of a two-dimensional turbulent wake. J. Fluid Mech. 693, 115–149.CrossRefGoogle Scholar
Parezanović, V., Monchaux, R. & Cadot, O. 2015 Characterization of the turbulent bistable flow regime of a 2 D bluff body wake disturbed by a small control cylinder. Exp. Fluids 56 (1), 12.CrossRefGoogle Scholar
Portela, F.A., Papadakis, G. & Vassilicos, J. 2017 The turbulence cascade in the near wake of a square prism. J. Fluid Mech. 825, 315–352.CrossRefGoogle Scholar
Prasad, A. & Williamson, C.H. 1997 Three-dimensional effects in turbulent bluff-body wakes. J. Fluid Mech. 343, 235–265.CrossRefGoogle Scholar
Reynolds, W. & Hussain, A. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.CrossRefGoogle Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10 (3), 345–356.CrossRefGoogle Scholar
Sakamoto, H. & Haniu, H. 1994 Optimum suppression of fluid forces acting on a circular cylinder. J. Fluids Eng. 116 (2), 221–227.CrossRefGoogle Scholar
Schmid, P.J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Sengupta, T. & Lekoudis, S. 1985 Calculation of two-dimensional turbulent boundary layers over rigid and moving wavy surfaces. AIAA J. 23 (4), 530–536.CrossRefGoogle Scholar
Sengupta, T.K., Singh, N. & Suman, V. 2010 Dynamical system approach to instability of flow past a circular cylinder. J. Fluid Mech. 656, 82–115.CrossRefGoogle Scholar
Song, F.-L., Lu, W.-T. & Kuo, C.-H. 2013 Interactions of lock-on wake behind side-by-side cylinders of unequal diameter at Reynolds number 600. Expl Therm. Fluid Sci. 44, 736–748.CrossRefGoogle Scholar
Strykowski, P.J. & Sreenivasan, K.R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
Williamson, C.H. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Wynn, A., Pearson, D., Ganapathisubramani, B. & Goulart, P.J. 2013 Optimal mode decomposition for unsteady flows. J. Fluid Mech. 733, 473–503.CrossRefGoogle Scholar
Yang, X. & Zebib, A. 1989 Absolute and convective instability of a cylinder wake. Phys. Fluids A: Fluid Dyn. 1 (4), 689–696.CrossRefGoogle Scholar
Yildirim, I., Rindt, C. & Steenhoven, A. 2010 Vortex dynamics in a wire-disturbed cylinder wake. Phys. Fluids 22 (9), 094101.CrossRefGoogle Scholar
Zhang, H.-Q., Fey, U., Noack, B.R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.CrossRefGoogle Scholar