Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-20T01:28:29.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Electrohydrodynamic rotation of drops at large electric Reynolds numbers

Published online by Cambridge University Press:  11 January 2016

Ehud Yariv  and
Itzchak Frankel
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
Itzchak Frankel
Affiliation:
Department of Aerospace Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When subject to sufficiently strong electric fields, particles and drops suspended in a weakly conducting liquid exhibit spontaneous rotary motion. This so-called Quincke rotation is a fascinating example of nonlinear symmetry-breaking phenomena. To illuminate the rotation of liquid drops we here analyse the asymptotic limit of large electric Reynolds numbers, 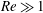$\mathit{Re}\gg 1$, within the framework of a two-dimensional Taylor–Melcher electrohydrodynamic model. A non-trivial dominant balance in this singular limit results in both the fluid velocity and surface-charge density scaling as 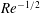$\mathit{Re}^{-1/2}$. The flow is governed by a self-contained nonlinear boundary-value problem that does not admit a continuous fore–aft symmetric solution, thus necessitating drop rotation. Furthermore, thermodynamic arguments reveal that a fore–aft asymmetric solution exists only when charge relaxation within the suspending liquid is faster than that in the drop. The flow problem possesses both mirror-image (with respect to the direction of the external field) and flow-reversal symmetries; it is transformed into a universal one, independent of the ratios of electric conductivities and dielectric permittivities in the respective drop phase and suspending liquid phase. The rescaled angular velocity is found to depend weakly upon the viscosity ratio. The corresponding numerical solutions of the exact equations indeed collapse at large 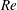$\mathit{Re}$ upon the asymptotically calculated universal solution.

JFM classification

Drops and Bubbles: Drops and Bubbles Drops and Bubbles: Electrohydrodynamic effects Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , R2
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O. & Bartolo, D. 2013 Emergence of macroscopic directed motion in populations of motile colloids. Nature 503 (7474), 95–98.Google Scholar
Cēbers, A. 2004 Bistability and negative viscosity for a suspension of insulating particles in an electric field. Phys. Rev. Lett. 92 (3), 034501.Google Scholar
Das, D. & Saintillan, D. 2013 Electrohydrodynamic interaction of spherical particles under Quincke rotation. Phy. Rev. E 87 (4), 043014.Google Scholar
Feng, J. Q. 2002 A 2D electrohydrodynamic model for electrorotation of fluid drops. J. Colloid Interface Sci. 246 (1), 112–121.Google Scholar
Ha, J.-W. & Yang, S.-M. 2000 Electrohydrodynamics and electrorotation of a drop with fluid less conductive than that of the ambient fluid. Phys. Fluids 12 (4), 764–772.Google Scholar
He, H., Salipante, P. F. & Vlahovska, P. M. 2013 Electrorotation of a viscous droplet in a uniform direct current electric field. Phys. Fluids 25 (3), 032106.Google Scholar
Jones, T. B. 1984 Quincke rotation of spheres. IEEE Trans. Ind. Applics. 4, 845–849.Google Scholar
Krause, S. & Chandratreya, P. 1998 Electrorotation of deformable fluid droplets. J. Colloid Interface Sci. 206 (1), 10–18.Google Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2015 Nonlinear electrohydrodynamics of slightly deformed oblate drops. J. Fluid Mech. 774, 245–266.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.CrossRefGoogle Scholar
Lemaire, E. & Lobry, L. 2002 Chaotic behavior in electro-rotation. Physica A 314 (1), 663–671.Google Scholar
Lemaire, E., Lobry, L., Pannacci, N. & Peters, F. 2008 Viscosity of an electro-rheological suspension with internal rotations. J. Rheol. 52 (3), 769–783.Google Scholar
Lobry, L. & Lemaire, E. 1999 Viscosity decrease induced by a DC electric field in a suspension. J. Electrostat. 47 (1), 61–69.Google Scholar
Melcher, J. R. & Taylor, G. I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1 (1), 111–146.Google Scholar
Pannacci, N., Lemaire, E. & Lobry, L. 2007a Rheology and structure of a suspension of particles subjected to Quincke rotation. Rheol. Acta 46 (7), 899–904.Google Scholar
Pannacci, N., Lobry, L. & Lemaire, E. 2007b How insulating particles increase the conductivity of a suspension. Phys. Rev. Lett. 99 (9), 094503.Google Scholar
Peters, F., Lobry, L. & Lemaire, E. 2005 Experimental observation of Lorenz chaos in the Quincke rotor dynamics. Chaos 15 (1), 013102.Google Scholar
Quincke, G. 1896 Ueber Rotationen im constanten electrischen Felde. Ann. Phys. Chem. 59, 417–486.Google Scholar
Salipante, P. F. & Vlahovska, P. M. 2010 Electrohydrodynamics of drops in strong uniform dc electric fields. Phys. Fluids 22, 112110.Google Scholar
Salipante, P. F. & Vlahovska, P. M. 2013 Electrohydrodynamic rotations of a viscous droplet. Phys. Rev. E 88 (4), 043003.Google Scholar
Taylor, G. 1966 Studies in electrohydrodynamics. I. The circulation produced in a drop by electrical field. Proc. R. Soc. Lond. A 291 (1425), 159–166.Google Scholar
Yariv, E. 2006 ‘Force-free’ electrophoresis? Phys. Fluids 18, 031702.Google Scholar
Yeo, K., Lushi, E. & Vlahovska, P. M. 2015 Collective dynamics in a binary mixture of hydrodynamically coupled microrotors. Phys. Rev. Lett. 114 (18), 188301.Google Scholar