Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T00:37:16.576Z Has data issue: false hasContentIssue false
  • English
  • Français

The effects of surface tension on the initial development of a free surface adjacent to an accelerated plate

Published online by Cambridge University Press:  30 June 2015

J. Uddin  and
D. J. Needham
J. Uddin*
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
D. J. Needham
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When a vertical rigid plate is uniformly accelerated horizontally from rest into an initially stationary layer of inviscid incompressible fluid, the free surface will undergo a deformation in the locality of the contact point. This deformation of the free surface will, in the early stages, cause a jet to rise up the plate. An understanding of the local structure of the free surface in the early stages of motion is vital in many situations, and has been developed in detail by King & Needham (J. Fluid Mech., vol. 268, 1994, pp. 89–101). In this work we consider the effects of introducing weak surface tension, characterized by the inverse Weber number 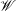$\mathscr{W}$, into the problem considered by King & Needham. Our approach is based upon matched asymptotic expansions as 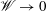$\mathscr{W}\rightarrow 0$. It is found that four asymptotic regions are needed to describe the problem. The three largest regions have analytical solutions, whilst a numerical method based on finite differences is used to solve the time-dependent harmonic boundary value problem in the last region. Our results identify the local structure of the jet near the vicinity of the contact point, and we highlight a number of key features, including the height of this jet as well as its thickness and strength. We also present some preliminary experimental results that capture the spatial structure near the contact point, and we then show promising comparisons with the theoretical results obtained within this paper.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Wakes/Jets: Jets Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 37 - 73
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chwang, A. T. 1983 Nonlinear hydrodynamic pressure on an accelerating plate. Phys. Fluids 26, 383–387.Google Scholar
Greenhow, M. 1993 A complex variable method for the floating body boundary value problem. J. Comput. Appl. Maths 46, 115.CrossRefGoogle Scholar
Howison, S. D., Ockendon, J. R., Oliver, J. M., Purvis, R. & Smith, F. T. 2005 Droplet impact on a thin fluid layer. J. Fluid Mech. 542, 1.CrossRefGoogle Scholar
Iafrati, A. & Korobkin, A. 2004 Initial stage of flat plate impact onto liquid free surface. Phys. Fluids 16, 2214.Google Scholar
Joo, S. W., Schultz, W. W. & Messiter, A. F. 1990 An analysis of the initial value wavemaker problem. J. Fluid Mech. 214, 161–183.Google Scholar
King, A. C. & Needham, D. J. 1994 The initial development of a jet caused by fluid, body and free-surface interaction. Part 1. A uniformly accelerating plate. J. Fluid Mech. 268, 89–101.Google Scholar
Korobkin, A. A. & Pukhnachov, V. V. 1988 Initial stage of water impact. Annu. Rev. Fluid Mech. 20, 159–185.Google Scholar
Korsukova, E.2014 An experimental study of the initial evolution of a fluid’s free surface when displaced by an accelerating plate. PhD thesis, Department of Civil Engineering, University of Nottingham.Google Scholar
Liu, D. & Lin, P. 2009 Three-dimensional liquid sloshing in a tank with baffles. Ocean Engng 36, 202–212.Google Scholar
Needham, D. J., Billingham, J. & King, A. C. 2007 The initial development of a jet caused by fluid, body and free-surface interaction. Part 2. An impulsively moved plate. J. Fluid Mech. 67, 67–84.Google Scholar
Needham, D. J., Chamberlain, P. G. & Billingham, J. 2008 The initial development of a jet caused by fluid, body and free-surface interaction. Part 3. An inclined accelerating plate. Q. J. Mech. Appl. Maths 61, 581–614.Google Scholar
Norkin, M. & Korobkin, A. 2011 The motion of the free-surface separation point during the initial stage of horizontal impulsive displacement of a floating circular cylinder. J. Engng Maths 70, 239–254.Google Scholar
Purvis, R. & Smith, F. T. 2005 Droplet impact on water layers: post impact analysis and computations. Proc. R. Soc. Lond. A 363, 1209–1221.Google Scholar
Rebouillat, S. & Liksonov, D. 2010 Fluid–structure interaction in partially filled liquid containers: a comparative review of numerical approaches. Comput. Fluids 39 (5), 739–746.Google Scholar
Roberts, A. J. 1987 Transient free-surface flows generated by a moving vertical plate. Q. J. Appl. Maths 40, 129–158.CrossRefGoogle Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. Parabolic.Google Scholar
Veldman, A. E. P., Gerrits, J., Luppes, R., Helder, J. A. & Vreeburg, J. P. B. 2007 The numerical simulation of liquid sloshing on board spacecraft. J. Comput. Phys. 224, 82–99.Google Scholar