Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T06:32:02.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of streamwise-elongated and spanwise-periodic surface roughness elements on boundary-layer instability

Published online by Cambridge University Press:  27 July 2020

Csaba B. Kátai Open the ORCID record for Csaba B. Kátai [Opens in a new window]  and
Xuesong Wu Open the ORCID record for Xuesong Wu [Opens in a new window]
Csaba B. Kátai*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, LondonSW7 2AZ, UK
Xuesong Wu
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, LondonSW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

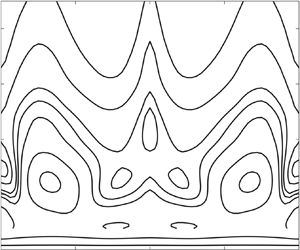
We investigate the impact on the boundary-layer stability of spanwise-periodic, streamwise-elongated surface roughness elements. Our interest is in their effects on the so-called lower-branch Tollmien–Schlichting modes, and so the spanwise spacing of the elements is taken to be comparable with the spanwise wavelength of the latter, which is of $O(R^{-3/8} L)$, where $L$ is the dimensional length from the leading edge of the flat plate to the surface roughness, and $R$ is the Reynolds number based on $L$. The streamwise length is much longer, consistent with experimental set-ups. The roughness height is chosen such that the wall shear is altered by $O(1)$. From the generic triple-deck theory for three-dimensional roughness elements with both the streamwise and spanwise length scales being of $O(R^{-3/8 }L)$, we derived the relevant governing equations by appropriate rescaling. The resulting equations are nonlinear but parabolic because the pressure gradient in the streamwise direction is negligible while in the spanwise direction it is completely determined by the roughness shape. Appropriate upstream, boundary and matching conditions are derived for the problem. Owing to the parabolicity, the equations are solved efficiently using a marching method to obtain the streaky flow. The instability of the streaky flow is shown to be controlled by the spanwise-dependent (periodic) wall shear. Two- and weakly three-dimensional lower-frequency modes are found to be stabilised by the streaks, confirming previous experimental findings, while stronger three-dimensional and higher-frequency modes are destabilised. Among the three roughness shapes considered, the roughness elements in the form of hemispherical caps are found to be most effective for a given height. A resonant subharmonic interaction was found to occur for modes with spanwise wavelength twice that of the roughness elements.

JFM classification

Boundary Layers: Boundary layer stability Flow Control: Instability control Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 899 , 25 September 2020 , A34
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Courier Corporation.Google Scholar
Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.CrossRefGoogle Scholar
Bagheri, S. & Hanifi, A. 2007 The stabilizing effect of streaks on Tollmien–Schlichting and oblique waves: A parametric study. Phys. Fluids 19 (7), 078103.CrossRefGoogle Scholar
Brown, S. N. 1985 Marginal separation of a three-dimensional boundary layer on a line of symmetry. J. Fluid Mech. 158, 95–111.CrossRefGoogle Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14 (8), L57–L60.CrossRefGoogle Scholar
Cossu, C. & Brandt, L. 2004 On Tollmien–Schlichting-like waves in streaky boundary layers. Eur. J. Mech. B/Fluids 23 (6), 815–833.CrossRefGoogle Scholar
Denissen, N. A. & White, E. B. 2013 Secondary instability of roughness-induced transient growth. Phys. Fluids 25 (11), 114108.CrossRefGoogle Scholar
Downs, R. S. & Fransson, J. H. M. 2014 Tollmien–Schlichting wave growth over spanwise-periodic surface patterns. J. Fluid Mech. 754, 39–74.CrossRefGoogle Scholar
Duck, P. W. & Burggraf, O. R. 1986 Spectral solutions for three-dimensional triple-deck flow over surface topography. J. Fluid Mech. 162, 1–22.CrossRefGoogle Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2004 Experimental and theoretical investigation of the nonmodal growth of steady streaks in a flat plate boundary layer. Phys. Fluids 16 (10), 3627–3638.CrossRefGoogle Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17 (5), 054110.CrossRefGoogle Scholar
Fransson, J. H. M. & Talamelli, A. 2012 On the generation of steady streamwise streaks in flat-plate boundary layers. J. Fluid Mech. 698, 211–234.CrossRefGoogle Scholar
Fransson, J. H. M., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96 (6), 064501.CrossRefGoogle ScholarPubMed
Gad-el Hak, M. 2000 Transition Control, pp. 104–119. Cambridge University Press.Google Scholar
Goldstein, M. E., Sescu, A., Duck, P. W. & Choudhari, M. 2010 The long range persistence of wakes behind a row of roughness elements. J. Fluid Mech. 644, 123–163.CrossRefGoogle Scholar
Goldstein, M. E., Sescu, A., Duck, P. W. & Choudhari, M. 2016 Nonlinear wakes behind a row of elongated roughness elements. J. Fluid Mech. 796, 516–557.CrossRefGoogle Scholar
Govindarajan, R. & Narasimha, R. 1997 A low-order theory for stability of non-parallel boundary layer flows. Proc. R. Soc. Lond. A 453 (1967), 2537–2549.CrossRefGoogle Scholar
Green, J. E. 2008 Laminar flow control – back to the future? AIAA Paper 2008-3738. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Hall, P. & Horseman, N. J. 1991 The linear inviscid secondary instability of longitudinal vortex structures in boundary layers. J. Fluid Mech. 232, 357–375.CrossRefGoogle Scholar
Hall, P. & Smith, F. T. 1990 Near-planar TS waves and longitudinal vortices in channel flow: Nonlinear interaction and focussing. In Instability and Transition (ed. Hussaini, M. Y. and Voigt, R. G.), pp.5–39. Springer.Google Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20 (1), 487–526.CrossRefGoogle Scholar
Joslin, R. D. 1998 Aircraft laminar flow control. Annu. Rev. Fluid Mech. 30 (1), 1–29.CrossRefGoogle Scholar
Kátai, C. B. 2020 Asymptotic description of transitional and turbulent flows: Effects of surface roughness on the boundary layer and the evolution of coherent structures in free shear flows. PhD thesis, Imperial College London.Google Scholar
Klebanoff, P. S. & Tidstrom, K. D. 1972 Mechanism by which a two-dimensional roughness element induces boundary-layer transition. Phys. Fluids 15 (7), 1173–1188.CrossRefGoogle Scholar
Li, F. & Malik, M. R. 1995 Fundamental and subharmonic secondary instabilities of Görtler vortices. J. Fluid Mech. 297, 77–100.CrossRefGoogle Scholar
Lin, C. C. 1945 On the stability of two-dimensional parallel flows. Part 3. Stability in a viscous fluid. Q. Appl. Maths 3 (4), 277–301.CrossRefGoogle Scholar
Luchini, P. 2000 Reynolds-number-independent instability of the boundary layer over a flat surface: Optimal perturbations. J. Fluid Mech. 404, 289–309.CrossRefGoogle Scholar
Messiter, A. F. 1970 Boundary-layer flow near the trailing edge of a flat plate. SIAM J. Appl. Maths 18 (1), 241–257.CrossRefGoogle Scholar
Muller, D. E. 1956 A method for solving algebraic equations using an automatic computer. Math. Tables Aids Comput. 10 (56), 208–215.CrossRefGoogle Scholar
Nayfeh, A. H., Ragab, S. A. & Al-Maaitah, A. A. 1988 Effect of bulges on the stability of boundary layers. Phys. Fluids 31 (4), 796–806.CrossRefGoogle Scholar
Neiland, V. Y. 1969 Theory of laminar boundary layer separation in supersonic flow. Fluid Dyn. 4 (4), 33–35.Google Scholar
Orszag, S. A. 1971 On the elimination of aliasing in finite-difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 28 (6), 1074–1074.2.0.CO;2>CrossRefGoogle Scholar
Piot, E., Casalis, G. & Rist, U. 2008 Stability of the laminar boundary layer flow encountering a row of roughness elements: Biglobal stability approach and DNS. Eur. J. Mech. B/Fluids 27 (6), 684–706.CrossRefGoogle Scholar
Prandtl, L. 1938 Zur Berechnung der Grenzschichten. Z. Angew. Math. Mech. 18 (1), 77–82.CrossRefGoogle Scholar
Reed, H. L. & Nayfeh, A. H. 1986 Numerical-perturbation technique for stability of flat-plate boundary layers with suction. AIAA J. 24 (2), 208–214.CrossRefGoogle Scholar
Reynolds, G. A. & Saric, W. S. 1986 Experiments on the stability of the flat-plate boundary layer with suction. AIAA J. 24 (2), 202–207.CrossRefGoogle Scholar
Ricco, P., Luo, J. & Wu, X. 2011 Evolution and instability of unsteady nonlinear streaks generated by free-stream vortical disturbances. J. Fluid Mech. 677, 1–38.CrossRefGoogle Scholar
Rozhko, S. B. & Ruban, A. I. 1987 Longitudinal-transverse interaction in a three-dimensional boundary layer. Fluid Dyn. 22 (3), 362–371.CrossRefGoogle Scholar
Rozhko, S. B., Ruban, A. I. & Timoshin, S. N. 1988 Interaction of a three-dimensional boundary layer with an extensive obstacle. Fluid Dyn. 23 (1), 30–37.CrossRefGoogle Scholar
Ruban, A. I. 1982 Asymptotic theory of short separation regions on the leading edge of a slender airfoil. Fluid Dyn. 17 (1), 33–41.CrossRefGoogle Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34 (1), 291–319.CrossRefGoogle Scholar
Sattarzadeh, S. S., Fransson, J. H. M., Talamelli, A. & Fallenius, B. E. G. 2014 Consecutive turbulence transition delay with reinforced passive control. Phys. Rev. E 89 (6), 061001.CrossRefGoogle ScholarPubMed
Shahinfar, S., Fransson, J. H. M., Sattarzadeh, S. S. & Talamelli, A. 2013 Scaling of streamwise boundary layer streaks and their ability to reduce skin-friction drag. J. Fluid Mech. 733, 1–32.CrossRefGoogle Scholar
Shahinfar, S., Sattarzadeh, S. S. & Fransson, J. H. M. 2014 Passive boundary layer control of oblique disturbances by finite-amplitude streaks. J. Fluid Mech. 749, 1–36.CrossRefGoogle Scholar
Shahinfar, S., Sattarzadeh, S. S., Fransson, J. H. M. & Talamelli, A. 2012 Revival of classical vortex generators now for transition delay. Phys. Rev. Lett. 109 (7), 074501.CrossRefGoogle ScholarPubMed
Siconolfi, L., Camarri, S. & Fransson, J. H. M. 2015 Stability analysis of boundary layers controlled by miniature vortex generators. J. Fluid Mech. 784, 596–618.CrossRefGoogle Scholar
Smith, F. T. 1979 a Instability of flow through pipes of general cross-section. Part 1. Mathematika 26 (2), 187–210.CrossRefGoogle Scholar
Smith, F. T. 1979 b On the non-parallel flow stability of the Blasius boundary layer. Proc. R. Soc. Lond. A 366, 91–109.Google Scholar
Smith, F. T., Brighton, P. W. M., Jackson, P. S. & Hunt, J. C. R. 1981 On boundary-layer flow past two-dimensional obstacles. J. Fluid Mech. 113, 123–152.CrossRefGoogle Scholar
Smith, F. T., Sykes, R. I. & Brighton, P. W. M. 1977 A two-dimensional boundary layer encountering a three-dimensional hump. J. Fluid Mech. 83 (1), 163–176.CrossRefGoogle Scholar
Stewartson, K. & Simpson, C. J. 1982 On a singularity initiating a boundary-layer collision. Q. J. Mech. Appl. Maths 35 (1), 1–16.CrossRefGoogle Scholar
Stewartson, K., Smith, F. T. & Kaups, K. 1982 Marginal separation. Stud. Appl. Maths 67 (1), 45–61.CrossRefGoogle Scholar
Stewartson, K. & Williams, P. G. 1969 Self-induced separation. Proc. R. Soc. Lond. A 312, 181–206.Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. The Parabolic Press.Google Scholar
Walsh, M. J. 1982 Turbulent boundary layer drag reduction using riblets. AIAA Paper 82-0169. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Walton, A. G. 1996 Strongly nonlinear vortex–Tollmien–Schlichting–wave interactions in the developing flow through a circular pipe. J. Fluid Mech. 319, 77–107.CrossRefGoogle Scholar
Walton, A. G. & Patel, R. A. 1998 On the neutral stability of spanwise-periodic boundary-layer and triple-deck flows. Q. J. Mech. Appl. Maths 51 (2), 311–328.CrossRefGoogle Scholar
White, E. B. 2002 Transient growth of stationary disturbances in a flat plate boundary layer. Phys. Fluids 14 (12), 4429–4439.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: Transmission coefficient as an eigenvalue. J. Fluid Mech. 794, 68–108.CrossRefGoogle Scholar
Wu, X. & Hogg, L. W. 2006 Acoustic radiation of Tollmien–Schlichting waves as they undergo rapid distortion. J. Fluid Mech. 550, 307–347.CrossRefGoogle Scholar
Xu, H., Lombard, J.-E. W. & Sherwin, S. J. 2017 a Influence of localised smooth steps on the instability of a boundary layer. J. Fluid Mech. 817, 138–170.CrossRefGoogle Scholar
Xu, H., Mughal, S. M., Gowree, E. R., Atkin, C. J. & Sherwin, S. J. 2017 b Destabilisation and modification of Tollmien–Schlichting disturbances by a three-dimensional surface indentation. J. Fluid Mech. 819, 592–620.CrossRefGoogle Scholar
Xu, H., Sherwin, S. J., Hall, P. & Wu, X. 2016 The behaviour of Tollmien–Schlichting waves undergoing small-scale localised distortions. J. Fluid Mech. 792, 499–525.CrossRefGoogle Scholar