Published online by Cambridge University Press: 01 August 2019
The influence of the nozzle-exit boundary-layer profile on high-subsonic jets is investigated by performing compressible large-eddy simulations (LES) for three isothermal jets at a Mach number of 0.9 and a diameter-based Reynolds number of 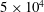 $5\times 10^{4}$, and by conducting linear stability analyses from the mean-flow fields. At the exit section of a pipe nozzle, the jets exhibit boundary layers of momentum thickness of approximately 2.8 % of the nozzle radius and a peak value of turbulence intensity of 6 %. The boundary-layer shape factors, however, vary and are equal to 2.29, 1.96 and 1.71. The LES flow and sound fields differ significantly between the first jet with a laminar mean exit velocity profile and the two others with transitional profiles. They are close to each other in these two cases, suggesting that similar results would also be obtained for a jet with a turbulent profile. For the two jets with non-laminar profiles, the instability waves in the near-nozzle region emerge at higher frequencies, the mixing layers spread more slowly and contain weaker low-frequency velocity fluctuations and the noise levels in the acoustic field are lower by 2–3 dB compared to the laminar case. These trends can be explained by the linear stability analyses. For the laminar boundary-layer profile, the initial shear-layer instability waves are most strongly amplified at a momentum-thickness-based Strouhal number
$5\times 10^{4}$, and by conducting linear stability analyses from the mean-flow fields. At the exit section of a pipe nozzle, the jets exhibit boundary layers of momentum thickness of approximately 2.8 % of the nozzle radius and a peak value of turbulence intensity of 6 %. The boundary-layer shape factors, however, vary and are equal to 2.29, 1.96 and 1.71. The LES flow and sound fields differ significantly between the first jet with a laminar mean exit velocity profile and the two others with transitional profiles. They are close to each other in these two cases, suggesting that similar results would also be obtained for a jet with a turbulent profile. For the two jets with non-laminar profiles, the instability waves in the near-nozzle region emerge at higher frequencies, the mixing layers spread more slowly and contain weaker low-frequency velocity fluctuations and the noise levels in the acoustic field are lower by 2–3 dB compared to the laminar case. These trends can be explained by the linear stability analyses. For the laminar boundary-layer profile, the initial shear-layer instability waves are most strongly amplified at a momentum-thickness-based Strouhal number 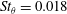 $St_{\unicode[STIX]{x1D703}}=0.018$, which is very similar to the value obtained downstream in the mixing-layer velocity profiles. For the transitional profiles, on the contrary, they predominantly grow at higher Strouhal numbers, around
$St_{\unicode[STIX]{x1D703}}=0.018$, which is very similar to the value obtained downstream in the mixing-layer velocity profiles. For the transitional profiles, on the contrary, they predominantly grow at higher Strouhal numbers, around 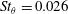 $St_{\unicode[STIX]{x1D703}}=0.026$ and 0.032, respectively. As a consequence, the instability waves rapidly vanish during the boundary-layer/shear-layer transition in the latter cases, but continue to grow over a large distance from the nozzle in the former case, leading to persistent large-scale coherent structures in the mixing layers for the jet with a laminar exit velocity profile.
$St_{\unicode[STIX]{x1D703}}=0.026$ and 0.032, respectively. As a consequence, the instability waves rapidly vanish during the boundary-layer/shear-layer transition in the latter cases, but continue to grow over a large distance from the nozzle in the former case, leading to persistent large-scale coherent structures in the mixing layers for the jet with a laminar exit velocity profile.