Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T19:56:06.131Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of matrix viscoelasticity on the lateral migration of a deformable drop in a wall-bounded shear

Published online by Cambridge University Press:  21 June 2013

Swarnajay Mukherjee  and
Kausik Sarkar
Swarnajay Mukherjee
Affiliation:
Department of Mechanical Engineering, University of Delaware, Newark, DE 19716, USA
Kausik Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, George Washington University, Washington, DC 20052, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of a drop deforming, orienting and moving in a shear flow of a viscoelastic liquid near a wall is numerically investigated using a front-tracking finite-difference method and a semi-analytic theory. The viscoelasticity is modelled using the modified FENE-CR constitutive equation. In a Newtonian system, deformation in a drop breaks the reversal symmetry of the system resulting in a migration away from the wall. This study shows that the matrix elasticity reduces the migration velocity, the reduction scaling approximately linearly with viscoelasticity (product of the Deborah number De and the ratio of polymer viscosity to total viscosity 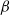$\beta $). Similar to a Newtonian system, for small Deborah numbers, the dynamics quickly reaches a quasi-steady state where deformation, inclination, as well as migration and slip velocities become independent of the initial drop–wall separation. They all approximately scale inversely with the square of the instantaneous separation except for deformation which scales inversely with the cube of separation. The deformation shows a non-monotonic variation with increasing viscoelasticity similar to the case of a drop in an unbounded shear and is found to influence little the change in migration. Two competing effects due to matrix viscoelasticity on drop migration are identified. The first stems from the reduced inclination angle of the drop with increasing viscoelasticity that tries to enhance migration velocity. However, it is overcome by the second effect inhibiting migration that results from the normal stress differences from the curved streamlines around the drop; they are more curved on the side away from the wall compared with those in the gap between the wall and the drop, an effect that is also present for a rigid particle. A perturbative theory of migration is developed for small ratio of the drop size to its separation from the wall that clearly shows the migration to be caused by the image stresslet field due to the drop in presence of the wall. The theory delineates the two competing viscoelastic effects, their relative magnitudes, and predicts migration that matches well with the simulation. Using the simulation results and the stresslet theory, we develop an algebraic expression for the quasi-steady migration velocity as a function of Ca, De and 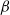$\beta $. The transient dynamics of the migrating drop is seen to be governed by the finite time needed for development of the viscoelastic stresses. For larger capillary numbers, in both Newtonian and viscoelastic matrices, a viscous drop fails to reach a quasi-steady state independent of initial drop–wall separation. Matrix viscoelasticity tends to prevent drop breakup. Drops that break up in a Newtonian matrix are stabilized in a viscoelastic matrix if it is initially far away from the wall. Initial proximity to the wall enhances deformation and aids in drop breakup.

JFM classification

Complex Fluids: Complex Fluids Drops and Bubbles: Drops Non-Newtonian Flows: Viscoelasticity
Type
Papers
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , pp. 318 - 345
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aggarwal, N. & Sarkar, K. 2007 Deformation and breakup of a viscoelastic drop in a Newtonian matrix under steady shear. J. Fluid Mech. 584, 1–21.CrossRefGoogle Scholar
Aggarwal, N. & Sarkar, K. 2008a Effects of matrix viscoelasticity on viscous and viscoelastic drop deformation in a shear flow. J. Fluid Mech. 601, 63–84.CrossRefGoogle Scholar
Aggarwal, N. & Sarkar, K. 2008b Rheology of an emulsion of viscoelastic drops in steady shear. J. Non-Newtonian Fluid Mech. 150, 19–31.CrossRefGoogle Scholar
Bartram, E., Goldsmith, H. L. & Mason, S. G. 1975 Particle motions in non-newtonian media III. Further observations in elasticoviscous fluids. Rheol. Acta 14, 776–782.CrossRefGoogle Scholar
Batchelor, G. K. 1970 Stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.CrossRefGoogle Scholar
Blake, J. R. 1971 A note on the image system for a stokeslet in a no-slip boundary. Proc. Camb. Phil. Soc. Math. Phys. Sci. 70, 303–310.Google Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14, 284–304.CrossRefGoogle Scholar
Cantat, I. & Misbah, C. 1999 Lift force and dynamical unbinding of adhering vesicles under shear flow. Phys. Rev. Lett. 83, 880–883.CrossRefGoogle Scholar
Chaffey, C. E., Brenner, H. & Mason, S. G. 1965 Particle motions in sheared suspensions XVIII: Wall migration. Rheol. Acta 4, 64–72.Google Scholar
Chan, P. C. H. & Leal, L. G. 1977 Note on motion of a spherical-particle in a general quadratic flow of a 2nd-order fluid. J. Fluid Mech. 82, 549–559.CrossRefGoogle Scholar
Chan, P. C. H. & Leal, L. G. 1979 The motion of a deformable drop in a second-order fluid. J. Fluid Mech. 92, 131–170.Google Scholar
Chilcott, M. D. & Rallison, J. M. 1988 Creeping flow of dilute polymer solutions past cylinders and spheres. J. Non-Newtonian Fluid Mech. 29, 381–432.Google Scholar
Coates, P. J., Armstrong, R. C. & Brown, R. A. 1992 Calculation of steady-state viscoelastic flow through axisymmetric contractions with the EEME formulation. J. Non-Newtonian Fluid Mech. 42, 141–188.Google Scholar
D’Avino, G., Maffettone, P. L., Greco, F. & Hulsen, M. A. 2010a Viscoelasticity-induced migration of a rigid sphere in confined shear flow. J. Non-Newtonian Fluid Mech. 165, 466–474.Google Scholar
D’Avino, G., Tuccillo, T., Maffettone, P. L., Greco, F. & Hulsen, M. A. 2010b Numerical simulations of particle migration in a viscoelastic fluid subjected to shear flow. Comput. Fluids 39, 709–721.Google Scholar
Dou, H.-S. & Phan-Thien, N. 2003 Negative wake in the uniform flow past a cylinder. Rheol. Acta 42, 383–409.Google Scholar
Elmendorp, J. J. & Maalcke, R. J. 1985 A study on polymer blending microrheology. 1. Polym. Engng Sci. 25, 1041–1047.Google Scholar
Feng, J. & Joseph, D. D. 1996 The motion of solid particles suspended in viscoelastic liquids under torsional shear. J. Fluid Mech. 324, 199–222.Google Scholar
Flumerfelt, R. W. 1972 Drop breakup in simple shear fields of viscoelastic fluids. Ind. Engng Chem. Fundam. 11, 312–318.CrossRefGoogle Scholar
Gauthier, F., Goldsmith, H. L. & Mason, S. G. 1971a Particle motions in non-Newtonian media I: Couette flow. Rheol. Acta 10, 344–364.Google Scholar
Gauthier, F., Goldsmith, H. L. & Mason, S. G. 1971b Particle motions in non-Newtonian media. II: Poiseuille flow. Trans. Soc. Rheol. 15, 297–330.Google Scholar
Goldsmith, H. L. & Mason, S. G. 1962 Flow of suspensions through tubes. 1. Single spheres, rods, and disks. J. Colloid Sci. 17, 448–476.Google Scholar
Hegler, R. P. & Mennig, G. 1985 Phase-separation effects in processing of glass-bead-filled and glass-fiber-filled thermoplastics by injection-molding. Polym. Engng Sci. 25, 395–405.Google Scholar
Ho, B. P. & Leal, L. G. 1976 Migration of rigid spheres in a 2-dimensional unidirectional shear-flow of a 2nd-order fluid. J. Fluid Mech. 76, 783–799.Google Scholar
Huang, P. Y., Feng, J., Hu, H. H. & Joseph, D. D. 1997 Direct simulation of the motion of solid particles in Couette and Poiseuille flows of viscoelastic fluids. J. Fluid Mech. 343, 73–94.Google Scholar
Imaeda, T. 2000 Shear-induced migration of a droplet in the presence of a plane wall. Physica A 285, 306–314.CrossRefGoogle Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. Ser. A 102, 161–179.Google Scholar
Joseph, D. D. & Feng, J. 1996 A note on the forces that move particles in a second-order fluid. J. Non-Newtonian Fluid Mech. 64, 299–302.Google Scholar
Karnis, A. & Mason, S. G. 1966 Particle motions in sheared suspensions. XIX. Viscoelastic media. Trans. Soc. Rheol. 10, 571–592.Google Scholar
Karnis, A. & Mason, S. G. 1967 Particle motions in sheared suspensions: XXIII. Wall migration of fluid drops. J. Colloid Interface Sci. 24, 164–169.Google Scholar
Kennedy, M. R., Pozrikidis, C. & Skalak, R. 1994 Motion and deformation of liquid-drops, and the rheology of dilute emulsions in simple shear-flow. Comput. Fluids 23, 251–278.Google Scholar
Kim, J. M., Kim, C., Chung, C., Ahn, K. H. & Lee, S. J. 2005 Negative wake generation of FENE-CR fluids in uniform and Poiseuille flows past a cylinder. Rheol. Acta 44, 600–613.Google Scholar
Leal, L. G. 1979 The motion of small particles in non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 5, 33–78.Google Scholar
Leal, L. G. 1980 Particle motions in a viscous-fluid. Annu. Rev. Fluid Mech. 12, 435–476.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport. Cambridge University Press.Google Scholar
Li, X. Y. & Sarkar, K. 2005a Drop dynamics in an oscillating extensional flow at finite Reynolds numbers. Phys. Fluids 17, 027103.Google Scholar
Li, X. Y. & Sarkar, K. 2005b Effects of inertia on the rheology of a dilute emulsion of drops in shear. J. Rheol. 49, 1377–1394.CrossRefGoogle Scholar
Li, X. Y. & Sarkar, K. 2005c Numerical investigation of the rheology of a dilute emulsion of drops in an oscillating extensional flow. J. Non-Newtonian Fluid Mech. 128, 71–82.Google Scholar
Li, X. Y. & Sarkar, K. 2006 Drop deformation and breakup in a vortex at finite inertia. J. Fluid Mech. 564, 1–23.Google Scholar
Lormand, B. M. & Phillips, R. J. 2004 Sphere migration in oscillatory Couette flow of a viscoelastic fluid. J. Rheol. 48, 551–570.Google Scholar
Ma, H. B. & Graham, M. D. 2005 Theory of shear-induced migration in dilute polymer solutions near solid boundaries. Phys. Fluids 17, 083103.CrossRefGoogle Scholar
Matos, H. M., Alves, M. A. & Oliveira, P. J. 2009 New formulation for stress calculation: application to viscoelastic flow in a T-junction. Numer. Heat Transfer B 56, 351–371.Google Scholar
Moyers-Gonzalez, M. & Frigaard, I. 2010 The critical wall velocity for stabilization of plane Couette–Poiseuille flow of viscoelastic fluids. J. Non-Newtonian Fluid Mech. 165, 441–447.Google Scholar
Mukherjee, S. & Sarkar, K. 2009 Effects of viscosity ratio on deformation of a viscoelastic drop in a Newtonian matrix under steady shear. J. Non-Newtonian Fluid Mech. 160, 104–112.Google Scholar
Mukherjee, S. & Sarkar, K. 2010 Effects of viscoelasticity on the retraction of a sheared drop. J. Non-Newtonian Fluid Mech. 165, 340–349.CrossRefGoogle Scholar
Mukherjee, S. & Sarkar, K. 2011 Viscoelastic drop falling through a viscous medium. Phys. Fluids 23, 013101.Google Scholar
Olapade, P. J., Singh, R. K. & Sarkar, K. 2009 Pair-wise interactions between deformable drops in free shear at finite inertia. Phys. Fluids 21, 063302.CrossRefGoogle Scholar
Oliveira, P. J. 2003 Asymmetric flows of viscoelastic fluids in symmetric planar expansion geometries. J. Non-Newtonian Fluid Mech. 114, 33–63.Google Scholar
Oliveira, P. J. & Miranda, A. l. I. P. 2005 A numerical study of steady and unsteady viscoelastic flow past bounded cylinders. J. Non-Newtonian Fluid Mech. 127, 51–66.Google Scholar
Philippoff, W. 1937 Viscosity characteristics of rubber solution. Rubber Chem. Tech. 10, 76–106.Google Scholar
Pillapakkam, S. B., Singh, P., Blackmore, D. & Aubry, N. 2007 Transient and steady state of a rising bubble in a viscoelastic fluid. J. Fluid Mech. 589, 215–252.Google Scholar
Ramaswamy, S. & Leal, L. G. 1999 The deformation of a viscoelastic drop subjected to steady uniaxial extensional flow of a Newtonian fluid. J. Non-Newtonian Fluid Mech. 85, 127–163.Google Scholar
Rocha, G. N., Poole, R. J. & Oliveira, P. J. 2007 Bifurcation phenomena in viscoelastic flows through a symmetric 1:4 expansion. J. Non-Newtonian Fluid Mech. 141, 1–17.CrossRefGoogle Scholar
Rosenkilde, C. E. 1967 Surface-energy tensors. J. Math. Phys. 8, 84–88.Google Scholar
Saffman, P. G. 1956 On the motion of small spheroidal particles in a viscous liquid. J. Fluid Mech. 1, 540–553.Google Scholar
Sahin, M. & Owens, R. G. 2004 On the effects of viscoelasticity on two-dimensional vortex dynamics in the cylinder wake. J. Non-Newtonian Fluid Mech. 123, 121–139.Google Scholar
Sarkar, K. & Schowalter, W. R. 2000 Deformation of a two-dimensional viscoelastic drop at non-zero Reynolds number in time-periodic extensional flows. J. Non-Newtonian Fluid Mech. 95, 315–342.CrossRefGoogle Scholar
Sarkar, K. & Schowalter, W. R. 2001 Deformation of a two-dimensional drop at non-zero Reynolds number in time-periodic extensional flows: numerical simulation. J. Fluid Mech. 436, 177–206.Google Scholar
Shapira, M. & Haber, S. 1990 Low Reynolds number motion of a droplet in shear flow including wall effects. Intl J. Multiphase Flow 16, 305–321.Google Scholar
Singh, R. K. & Sarkar, K. 2011 Inertial effects on the dynamics, streamline topology and interfacial stresses due to a drop in shear. J. Fluid Mech. 683, 149–171.Google Scholar
Smart, J. R. & Leighton, D. T. Jr. 1991 Measurement of the drift of a droplet due to the presence of a plane. Phys. Fluids A 3, 21–28.CrossRefGoogle Scholar
Szabo, P., Rallison, J. M. & Hinch, E. J. 1997 Start-up of flow of a FENE-fluid through a 4:1:4 constriction in a tube. J. Non-Newtonian Fluid Mech. 72, 73–86.Google Scholar
Tavgac, T. 1972 Drop deformation and breakup in simple shear fields. PhD thesis, Chemical Engineering, Univ. of Houston, Texas.Google Scholar
Tangelder, G. J., Teirlinck, H. C., Slaaf, D. W. & Reneman, R. S. 1985 Distribution of blood-platelets flowing in arterioles. Am. J. Physiol. 248 (3), H318–H323.Google Scholar
Tretheway, D. C. & Leal, L. G. 2001 Deformation and relaxation of Newtonian drops in planar extensional flows of a Boger fluid. J. Non-Newtonian Fluid Mech. 99, 81–108.Google Scholar
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Al-Rawahi, N., Tauber, W., Han, J., Nas, S. & Jan, Y. J. 2001 A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 169, 708–759.Google Scholar
Uijttewaal, W. S. J., Nijhof, E. J. & Heethar, R. M. 1993 Droplet migration, deformation, and orientation in the presence of a plane wall: a numerical study compared with analytical theories. Phys. Fluids A 5, 819–825.CrossRefGoogle Scholar
Yue, P. T., Feng, J. J., Liu, C. & Shen, J. 2005 Viscoelastic effects on drop deformation in steady shear. J. Fluid Mech. 540, 427–437.Google Scholar