Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T15:22:58.931Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of helicity on dissipation in homogeneous box turbulence

Published online by Cambridge University Press:  28 September 2018

Moritz Linkmann Open the ORCID record for Moritz Linkmann [Opens in a new window]
Moritz Linkmann*
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, 35032 Marburg, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dimensionless dissipation coefficient 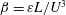$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L/U^{3}$, where $\unicode[STIX]{x1D700}$ is the dissipation rate, 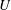$U$ the root-mean-square velocity and 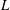$L$ the integral length scale, is an important characteristic of statistically stationary homogeneous turbulence. In studies of 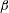$\unicode[STIX]{x1D6FD}$, the external force is typically isotropic and large scale, and its helicity 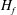$H_{f}$ either zero or not measured. Here, we study the dependence of 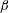$\unicode[STIX]{x1D6FD}$ on 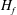$H_{f}$ and find that it decreases 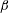$\unicode[STIX]{x1D6FD}$ by up to 10 % for both isotropic forces and shear flows. The numerical finding is supported by static and dynamical upper bound theory. Both show a relative reduction similar to the numerical results. That is, the qualitative and quantitative dependence of 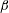$\unicode[STIX]{x1D6FD}$ on the helicity of the force is well captured by upper bound theory. Consequences for the value of the Kolmogorov constant and theoretical aspects of turbulence control and modelling are discussed in connection with the properties of the external force. In particular, the eddy viscosity in large-eddy simulations of homogeneous turbulence should be decreased by at least 10 % in the case of strongly helical forcing.

JFM classification

Turbulent Flows: Homogeneous turbulence Mathematical Foundations: Mathematical Foundations Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 79 - 102
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2017 Helically decomposed turbulence. J. Fluid Mech. 812, 752–770.Google Scholar
Baerenzung, J., Politano, H., Ponty, Y. & Pouquet, A. 2008 Spectral modeling of turbulent flows and the role of helicity. Phys. Rev. E 77, 046303.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence, 1st edn. Cambridge University Press.Google Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108, 164501.Google Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2013 Split energy-helicity cascades in three dimensional homogeneous and isotropic turbulence. J. Fluid Mech. 730, 309–327.Google Scholar
Biferale, L. & Titi, E. S. 2013 On the global regularity of a helical-decimated version of the 3D Navier–Stokes equation. J. Stat. Phys. 151, 1089–1098.Google Scholar
Bos, W. J. T. & Rubinstein, R. 2017 Dissipation in unsteady turbulence. Phys. Rev. Fluids. 2, 022601(R).Google Scholar
Bos, W. J. T., Shao, L. & Bertoglio, J.-P. 2007 Spectral imbalance and the normalized dissipation rate of turbulence. Phys. Fluids 19, 45101.Google Scholar
Brandenburg, A. 2001 The inverse cascade and nonlinear alpha-effect in simulations of isotropic helical magnetohydrodynamic turbulence. Astrophys. J. 550, 824–840.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. 2005 On the normalised turbulence energy dissipation rate. Phys. Fluids 17, 98103.Google Scholar
Busse, F. 1978 The optimum theory of turbulence. Adv. Appl. Mech. 18, 77–121.Google Scholar
Chen, Q., Chen, S. & Eyink, G. L. 2003a The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15, 361–374.Google Scholar
Chen, Q., Chen, S., Eyink, G. L. & Holm, D. D. 2003b Intermittency in the joint cascade of energy and helicity. Phys. Rev. Lett. 90, 214503.Google Scholar
Childress, S. 1970 New solutions of the kinematic dynamo problem. J. Math. Phys. 11, 3063–3076.Google Scholar
Childress, S., Kerswell, R. R. & Gilbert, A. D. 2001 Bounds on dissipation for Navier–Stokes flow with Kolmogorov forcing. Physica D 158 (1), 105–128.Google Scholar
Constantin, P. & Foias, C. 1988 Navier–Stokes Equations. University of Chicago Press.Google Scholar
Constantin, P. & Majda, A. 1988 The Beltrami spectrum for incompressible flows. Commun. Math. Phys. 115, 435–456.Google Scholar
Deusebio, E. & Lindborg, E. 2014 Helicity in the Ekman boundary layer. J. Fluid Mech. 755, 654–671.Google Scholar
Doering, C. R. & Constantin, P. 1994 Variational bounds on energy dissipation in incompressible flows: shear flow. Phys. Rev. E 49, 4087–4099.Google Scholar
Doering, C. R., Eckhardt, B. & Schumacher, J. 2003 Energy dissipation in body-forced plane shear flow. J. Fluid Mech. 494, 275–284.Google Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.Google Scholar
Doering, C. R. & Gibbon, J. D. 1995 Applied Analysis of the Navier–Stokes Equations. Cambridge University Press.Google Scholar
Doering, C. R. & Petrov, N. P. 2005 Low-wavenumber forcing and turbulent energy dissipation. In Progress in Turbulence (ed. Oberlack, M., Peinke, J., Kittel, A. & Barth, S.), Springer Proc. Physics, vol. 101, pp. 11–18. Springer.Google Scholar
Dombre, T., Frisch, U., Greene, J. M., Hénon, M., Mehr, A. & Soward, A. M. 1986 Chaotic streamlines in the ABC flows. J. Fluid Mech. 167, 353–391.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2005 Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J. Fluid Mech. 532, 199–216.Google Scholar
Eyink, G. L. 2003 Local 4/5-law and energy dissipation anomaly in turbulence. Nonlinearity 16, 137–145.Google Scholar
Foias, C., Manley, O., Rosa, R. & Temam, R. 2001 Navier–Stokes Equations and Turbulence, Encyclopedia of Mathematics and its Applications, vol. 83. Cambridge University Press.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of Kolmogorov. Cambridge University Press.Google Scholar
Gledzer, E. B. & Chkhetiani, O. G. 2015 Inverse energy cascade in developed turbulence at the breaking of the symmetry of helical modes. JETP Lett. 102, 465–472.Google Scholar
Goto, S. & Vassilicos, J. C. 2009 The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure. Phys. Fluids 21, 035104.Google Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 1065.Google Scholar
Howard, L. N. 1972 Bounds on flow quantities. Annu. Rev. Fluid Mech. 4, 473–494.Google Scholar
Inagaki, K., Yokoi, N. & Hamba, F. 2017 Mechanism of mean flow generation in rotating turbulence through inhomogeneous helicity. Phys. Rev. Fluids 2, 114605.Google Scholar
Ishihara, T., Morishita, K., Yokokawa, M., Uno, A. & Kaneda, Y. 2016 Energy spectrum in high-resolution direct numerical simulations of turbulence. Phys. Rev. Fluids 1, 082403(R).Google Scholar
Kaneda, Y., Ishihara, T., Yokokawa, M., Itakura, K. & Uno, A. 2003 Energy dissipation and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box. Phys. Fluids 15, L21.Google Scholar
Kerswell, R. R. 1998 Unification of variational principles for turbulent shear flows: the background method of Doering–Constantin and the mean-fluctuation formulation of Howard–Busse. Physica D 121 (1), 175–192.Google Scholar
Kessar, M., Plunian, F., Stepanov, R. & Balarac, G. 2015 Non-Kolmogorov cascade of helicity-driven turbulence. Phys. Rev. E 92, 031004(R).Google Scholar
Kraichnan, R. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59, 745–752.Google Scholar
Ladyshenskaya, O. A. 1969 The Mathematical Theory of Viscous Incompressible Flow, 2nd edn. Gordon and Breach.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics, English edn. Pergamon Press.Google Scholar
Leray, J. 1934 Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Mathematica 63, 193–248.Google Scholar
Li, Y., Meneveau, C., Chen, S. & Eyink, G. L. 2006 Subgrid-scale modeling of helicity and energy dissipation in helical turbulence. Phys. Rev. E 74, 026310.Google Scholar
Lilly, D. K. 1967 The representation of small scale turbulence in numerical simulation experiments. Proc. IBM Scientific Computing Symposium on Environmental Sciences (ed. Goldstine, H. H.), pp. 195–210. International Business Machines Corporation (IBM).Google Scholar
Lilly, D. K. 1986 The structure, energetics, and propagation of rotating convective storms. Part II. Helicity and storm stabilization. J. Atmos. Sci. 43, 126.Google Scholar
Lumley, J. L. 1992 Some comments on turbulence. Phys. Fluids A 4, 203–211.Google Scholar
McComb, W. D., Berera, A., Salewski, M. & Yoffe, S. R. 2010 Taylor’s (1935) dissipation surrogate reinterpreted. Phys. Fluids 22, 61704.Google Scholar
McComb, W. D., Berera, A., Yoffe, S. R. & Linkmann, M. F. 2015 Energy transfer and dissipation in forced isotropic turbulence. Phys. Rev. E 91, 043013.Google Scholar
Mininni, P. D. & Pouquet, A. G. 2010a Rotating helical turbulence. Part I. Global evolution and spectral behavior. Phys. Fluids 22, 035105.Google Scholar
Mininni, P. D. & Pouquet, A. G. 2010b Rotating helical turbulence. Part II. Intermittency, scale invariance, and structures. Phys. Fluids 22, 035106.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Moffatt, H. K. 1985 Magnetostatic equilibria and analogous Euler flows of arbitrarily complex topology. Part 1. Fundamentals. J. Fluid Mech. 159, 359–378.Google Scholar
Moffatt, H. K. 2014 Helicity and singular structures in fluid dynamics. Proc. Natl Acad. Sci. USA 111 (10), 3663–3670.Google Scholar
Nicodemus, R., Grossmann, S. & Holthaus, M. 1998 The background flow method. Part 1. Constructive approach to bounds on energy dissipation. J. Fluid Mech. 363, 281–300.Google Scholar
Polifke, W. & Shtilman, L. 1989 The dynamics of helical decaying turbulence. Phys. Fluids A 1, 2025–2033.Google Scholar
Rollin, B., Dubief, Y. & Doering, C. R. 2011 Variations on Kolmogorov flow: turbulent energy dissipation and mean flow profiles. J. Fluid Mech. 670, 204–213.Google Scholar
Sahoo, G. & Biferale, L. 2015 Disentangling the triadic interactions in Navier–Stokes equations. Eur. Phys. J. E 38, 1–8.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. Mon. Weath. Rev. 91, 99.Google Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence dissipation rate. Phys. Fluids 27, 1048–1051.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.Google Scholar
Stepanov, R., Golbraikh, E., Frick, P. & Shestakov, A. 2015 Hindered energy cascade in highly helical isotropic turbulence. Phys. Rev. Lett. 115, 234501.Google Scholar
Tannehill, J. C., Anderson, D. A. & Pletcher, R. A. 1997 Computational Fluid Mechanics and Heat Transfer, 2nd edn. Taylor & Francis.Google Scholar
Valente, P. C., Onishi, R. & da Silva, C. B. 2014 Origin of the imbalance between energy cascade and dissipation in turbulence. Phys. Rev. E 90, 023003.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for nonequilibrium turbulence. Phys. Rev. Lett. 108, 214503.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids A 4, 350–363.Google Scholar
Wang, L.-P., Chen, S., Brasseur, J. G. & Wyngaard, J. C. 1996 Examination of hypotheses in the Kolmogorov refined turbulence theory through high-resolution simulations. Part 1. Velocity field. J. Fluid Mech. 309, 113–156.Google Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2012 Dissipation, enstrophy and pressure statistics in turbulence simulations at high Reynolds numbers. J. Fluid Mech. 700, 5–15.Google Scholar
Yeung, P. K., Zhai, X. M. & Sreenivasan, K. R. 2015 Extreme events in computational turbulence. Proc. Natl Acad. Sci. USA 112, 12633–12638.Google Scholar
Yokoi, N. & Yoshizawa, A. 1993 Statistical analysis of the effects of helicity in inhomogeneous turbulence. Phys. Fluids A 5, 464–477.Google Scholar