Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T17:15:34.644Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of wall-normal gravity on particle-laden near-wall turbulence

Published online by Cambridge University Press:  25 June 2019

Junghoon Lee  and
Changhoon Lee Open the ORCID record for Changhoon Lee [Opens in a new window]
Junghoon Lee
Affiliation:
Department of Computational Science and Engineering, Yonsei University, Seoul 03722, Korea
Changhoon Lee*
Affiliation:
Department of Computational Science and Engineering, Yonsei University, Seoul 03722, Korea Department of Mechanical Engineering, Yonsei University, Seoul 03722, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We performed two-way coupled direct numerical simulations of turbulent channel flow with Lagrangian tracking of small, heavy spheres at a dimensionless gravitational acceleration of 0.077 in wall units, which is based on the flow condition in the experiment by Gerashchenko et al. (J. Fluid Mech., vol. 617, 2008, pp. 255–281). We removed deposited particles after several collisions with the lower wall and then released new particles near the upper wall to observe direct interactions between particles and coherent structures of near-wall turbulence during gravitational settling through the mean shear. 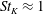The results indicate that when the Stokes number is approximately 1 on the basis of the Kolmogorov time scale of the flow ($St_{K}\approx 1$), the so-called preferential sweeping occurs in association with coherent streamwise vortices, while the effect of crossing trajectories becomes significant for 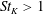$St_{K}>1$. Consequently, in either case, the settling particles deposit on the wall without strong accumulation in low-speed streaks in the viscous sublayer. When particles settle through near-wall turbulence from the upper wall, more small-scale vortical structures are generated in the outer layer as low-speed fluid is pulled farther in the direction of gravity, while the opposite is true near the lower wall.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 475 - 507
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelsamie, A. H. & Lee, C. 2012 Decaying versus stationary turbulence in particle-laden isotropic turbulence: turbulence modulation mechanism. Phys. Fluids 24, 015106.Google Scholar
Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2013 The effect of large-scale turbulent structures on particle dispersion in wall-bounded flows. Intl J. Multiphase Flow 51, 55–64.Google Scholar
Boivin, M., Simonin, O. & Squires, K. D. 1998 Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. J. Fluid Mech. 375, 235–263.Google Scholar
Bosse, T., Kleiser, L. & Meiburg, E. 2006 Small particles in homogeneous turbulence: settling velocity enhancement by two-way coupling. Phys. Fluids 18, 027102.Google Scholar
Capecelatro, J. & Desjardins, O. 2013 An Euler–Lagrange strategy for simulating particle-laden flows. Comput. Phys. 238, 1–31.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2016 Effect of domain size on fluid–particle statistics in homogeneous, gravity-driven, cluster-induced turbulence. J. Fluids Engng 138, 041301.Google Scholar
Choi, J.-I., Yeo, K. & Lee, C. 2004 Lagrangian statistics in turbulent channel flow. Phys. Fluids 16, 779–793.Google Scholar
Csanady, G. T. 1963 Turbulent diffusion of heavy particles in the atmosphere. J. Atmos. Sci. 20, 201–208.Google Scholar
DeMarchis, M., Milici, B. & Napoli, E. 2017 Solid sediment transport in turbulent channel flow over irregular rough boundaries. Intl J. Heat Fluid Flow 65, 114–126.Google Scholar
Dorgan, A. J. & Loth, E. 2004 Simulation of particles released near the wall in a turbulent boundary layer. Intl J. Multiphase Flow 30, 649–673.Google Scholar
Dorgan, A. J., Loth, E., Bocksell, T. L. & Yeung, P. K. 2005 Boundary-layer dispersion of near-wall injected particles of various inertias. AIAA J. 43, 1537–1548.Google Scholar
Dritselis, C. D. & Vlachos, N. S. 2008 Numerical study of educed coherent structures in the near-wall region of a particle-laden channel flow. Phys. Fluids 20, 055103.Google Scholar
Dritselis, C. D. & Vlachos, N. S. 2011 Numerical investigation of momentum exchange between particles and coherent structures in low Re turbulent channel flow. Phys. Fluids 23, 025103.Google Scholar
Eaton, J. K. 2009 Two-way coupled turbulence simulations of gas-particle flows using point-particle tracking. Intl J. Multiphase Flow 35, 792–800.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1992 Direct simulation of particle dispersion in a decaying isotropic turbulence. J. Fluid Mech. 242, 655–700.Google Scholar
Ferrante, A. & Elghobashi, S. 2003 On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 15, 315–329.Google Scholar
Gerashchenko, S., Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2008 Lagrangian measurements of inertial particle accelerations in a turbulent boundary layer. J. Fluid Mech. 617, 255–281.Google Scholar
Gualtieri, P., Battista, F. & Casciola, C. M. 2017 Turbulence modulation in heavy-loaded suspensions of tiny particles. Phys. Rev. Fluids 2, 034304.Google Scholar
Gualtieri, P., Picano, F., Sardina, G. & Casciola, C. M. 2013 Clustering and turbulence modulation in particle-laden shear flows. J. Fluid Mech. 715, 134–162.Google Scholar
Gualtieri, P., Picano, F., Sardina, G. & Casciola, C. M. 2015 Exact regularized point particle method for multiphase flows in the two-way coupling regime. J. Fluid Mech. 773, 520–561.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1998 The effect of particles on wall turbulence. Intl J. Multiphase Flow 24, 359–386.Google Scholar
Kiger, K. T. & Pan, C. 2002 Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 3, N19.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kussin, J. & Sommerfeld, M. 2002 Experimental studies on particle behaviour and turbulence modification in horizontal channel flow with different wall roughness. Exp. Fluids 33, 143–159.Google Scholar
Lavezzo, V., Soldati, A., Gerashchenko, S., Warhaft, Z. & Collins, L. R. 2010 On the role of gravity and shear on inertial particle accelerations in near-wall turbulence. J. Fluid Mech. 658, 229–246.Google Scholar
Lee, J. & Lee, C. 2015 Modification of particle-laden near-wall turbulence: Effect of Stokes number. Phys. Fluids 27, 023303.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Li, D., Luo, K. & Fan, J. 2016a Modulation of turbulence by dispersed solid particles in a spatially developing flat-plate boundary layer. J. Fluid Mech. 802, 359–394.Google Scholar
Li, D., Wei, A., Luo, K. & Fan, J. 2016b Direct numerical simulation of a particle-laden flow in a flat plate boundary layer. Intl J. Multiphase Flow 79, 124–143.Google Scholar
Li, J., Wang, H., Liu, Z., Chen, S. & Zheng, C. 2012 An experimental study on turbulence modification in the near-wall boundary layer of a dilute gas-particle channel flow. Exp. Fluids 53, 1385–1403.Google Scholar
Li, Y., McLaughlin, J. B., Kontomaris, K. & Portela, L. 2001 Numerical simulation of particle-laden turbulent channel flow. Phys. Fluids 13, 2957–2967.Google Scholar
Liu, B. Y. H. & Agarwal, J. K. 1974 Experimental observation of aerosol deposition in turbulent flow. Aerosol Sci. 5, 145–155.Google Scholar
Marchioli, C., Giusti, A., Salvetti, M. V. & Soldati, A. 2003 Direct numerical simulation of particle wall transfer and deposition in upward turbulent pipe flow. Intl J. Multiphase Flow 29, 1017–1038.Google Scholar
Marchioli, C., Picciotto, M. & Soldati, A. 2007 Influence of gravity and lift on particle velocity statistics and transfer rates in turbulent vertical channel flow. Intl J. Multiphase Flow 33, 227–251.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
Maxey, M. R. & Patel, B. K. 2001 Localized force representations for particles sedimenting in stokes flow. Intl J. Multiphase Flow 27, 1603–1626.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
Mito, Y. & Hanratty, T. J. 2006 Effect of feedback and inter-particle collisions in an idealized gas–liquid annular flow. Intl J. Multiphase Flow 32, 692–716.Google Scholar
Narayanan, C., Lakehal, D., Botto, L. & Soldati, A. 2003 Mechanisms of particle deposition in a fully developed turbulent open channel flow. Phys. Fluids 15, 763–775.Google Scholar
Nasr, H., Ahmadi, G. & McLaughlin, J. B. 2009 A DNS study of effects of particle–particle collisions and two-way coupling on particle deposition and phasic fluctuations. J. Fluid Mech. 640, 507–536.Google Scholar
Oresta, P. & Prosperetti, A. 2013 Effects of particle settling on Rayleigh–Bénard convection. Phys. Rev. E 87, 063014.Google Scholar
Pan, Y. & Banerjee, S. 1996 Numerical simulation of particle interactions with wall turbulence. Phys. Fluids 8, 2733–2755.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37, 341–383.Google Scholar
Park, H. J., O’Keefe, K. & Richter, D. H. 2018 Rayleigh–Bénard turbulence modified by two-way coupled inertial, nonisothermal particles. Phys. Rev. Fluids 3, 034307.Google Scholar
Park, Y. & Lee, C. 2014 Gravity-driven clustering of inertial particles in turbulence. Phys. Rev. E 89, 061004(R).Google Scholar
Pedinotti, S., Mariotti, G. & Banerjee, S. 1992 Direct numerical simulation of particle behaviour in the wall region of turbulent flows in horizontal channels. Intl J. Multiphase Flow 18, 927–941.Google Scholar
Picciotto, M., Marchioli, C., Reeks, M. W. & Soldati, A. 2005 Statistics of velocity and preferential accumulation of micro-particles in boundary layer turbulence. Nucl. Engng Des. 235, 1239–1249.Google Scholar
Rashidi, M. & Banerjee, S. 1990 The effect of boundary conditions and shear rate on streak formation and breakdown in turbulent channel flows. Phys. Fluids A 2, 1827–1838.Google Scholar
Rashidi, M., Hetsroni, G. & Banerjee, S. 1990 Particle-turbulence interaction in a boundary layer. Intl J. Multiphase Flow 16, 935–949.Google Scholar
Reeks, M. W. 1977 On the dispersion of small particles suspended in an isotropic turbulent fluid. J. Fluid Mech. 83, 529–546.Google Scholar
Richter, D. H. 2015 Turbulence modification by inertial particles and its influence on the spectral energy budget in planar Couette flow. Phys. Fluids 27, 063304.Google Scholar
Richter, D. H., Garcia, O. & Astephen, C. 2016 Particle stresses in dilute, polydisperse, two-way coupled turbulent flows. Phys. Rev. E 93, 013111.Google Scholar
Richter, D. H. & Sullivan, P. P. 2013 Momentum transfer in a turbulent, particle-laden Couette flow. Phys. Fluids 25, 053304.Google Scholar
Richter, D. H. & Sullivan, P. P. 2014 Modification of near-wall coherent structures by inertial particles. Phys. Fluids 26, 103304.Google Scholar
Righetti, M. & Romano, G. P. 2004 Particle–fluid interactions in a plane near-wall turbulent flow. J. Fluid Mech. 505, 93–121.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Rosa, B., Parishani, H., Ayala, O. & Wang, L.-P. 2016 Settling velocity of small inertial particles in homogeneous isotropic turbulence from high-resolution DNS. Intl J. Multiphase Flow 83, 217–231.Google Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.Google Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35, 827–839.Google Scholar
Soldati, A. & Marchioli, C. 2012 Sediment transport in steady turbulent boundary layers: potentials, limitations, and perspectives for Lagrangian tracking DNS and LES. Adv. Water Resour. 48, 18–30.Google Scholar
Tanière, A., Oesterlé, B. & Monnier, J. C. 1997 On the behaviour of solid particles in a horizontal boundary layer with turbulence and saltation effects. Exp. Fluids 23, 463–471.Google Scholar
Tsuji, Y. & Morikawa, Y. 1982 LDV measurements of an air–solid two-phase flow in a horizontal pipe. J. Fluid Mech. 120, 385–409.Google Scholar
Wang, G. & Richter, D. H. 2019 Modulation of the turbulence regeneration cycle by inertial particles in planar Couette flow. J. Fluid Mech. 861, 901–929.Google Scholar
Wang, L.-P., Ayala, O. & Grabowski, W. W. 2007 Effects of aerodynamic interactions on the motion of heavy particles in a bidisperse suspension. J. Turbul. 8, N25.Google Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wells, M. R. & Stock, D. E. 1983 The effects of crossing trajectories on the dispersion of particles in a turbulent flow. J. Fluid Mech. 136, 31–62.Google Scholar
Wu, Y., Wang, H., Liu, Z., Li, J., Zhang, L. & Zheng, C. 2006 Experimental investigation on turbulence modification in a horizontal channel flow at relatively low mass loading. Acta Mech. Sin. 22, 99–108.Google Scholar
Yang, C. Y. & Lei, U. 1998 The role of the turbulent scales in the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 371, 179–205.Google Scholar
Yang, T. S. & Shy, S. S. 2003 The settling velocity of heavy particles in an aqueous near-isotropic turbulence. Phys. Fluids 15, 868–880.Google Scholar
Yang, T. S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.Google Scholar
Yudine, M. I. 1959 Physical considerations on heavy-particle dispersion. Adv. Geophys. 6, 185–191.Google Scholar
Zhang, H. & Ahmadi, G. 2000 Aerosol particle transport and deposition in vertical and horizontal turbulent duct flows. J. Fluid Mech. 406, 55–80.Google Scholar
Zhao, L., Andersson, H. I. & Gillissen, J. J. J. 2013 Interphasial energy transfer and particle dissipation in particle-laden wall turbulence. J. Fluid Mech. 715, 32–59.Google Scholar
Zhao, L. H., Andersson, H. I. & Gillissen, J. J. J. 2010 Turbulence modulation and drag reduction by spherical particles. Phys. Fluids 22, 081702.Google Scholar