Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Wenjiang
Huang, Haibo
and
Lu, Xi-Yun
2020.
Optimal chordwise stiffness distribution for self-propelled heaving flexible plates.
Physics of Fluids,
Vol. 32,
Issue. 11,
Liu, Kui
Huang, Haibo
and
Lu, Xi-Yun
2020.
Hydrodynamic benefits of intermittent locomotion of a self-propelled flapping plate.
Physical Review E,
Vol. 102,
Issue. 5,
Lin, Xingjian
Wu, Jie
and
Zhang, Tongwei
2021.
Effect of torsional spring and shape on the performance of bioinspired caudal fin.
Physics of Fluids,
Vol. 33,
Issue. 7,
Li, Guojun
Kemp, Gaël
Jaiman, Rajeev Kumar
and
Khoo, Boo Cheong
2021.
A high-fidelity numerical study on the propulsive performance of pitching flexible plates.
Physics of Fluids,
Vol. 33,
Issue. 5,
Wang, Wenjiang
Huang, Haibo
and
Lu, Xi-Yun
2021.
Interplay of chordwise stiffness and shape on performance of self-propelled flexible flapping plate.
Physics of Fluids,
Vol. 33,
Issue. 9,
Yao, L.
Hefler, C.
Shyy, W.
and
Qiu, H. H.
2021.
Effects of gradual flexibility and trailing edge shape on propulsive performance of pitching fins.
Physics of Fluids,
Vol. 33,
Issue. 7,
Li, Yongcheng
Pan, Ziying
and
Zhang, Nan
2021.
Propulsive properties of a flexible oscillating wing with time-varying camber deformation.
Ocean Engineering,
Vol. 235,
Issue. ,
p.
109332.
Ezoji, Mojtaba
Shabakhty, Naser
and
Tao, Longbin
2022.
Hydrodynamic damping of solid and perforated heave plates oscillating at low KC number based on experimental data: A review.
Ocean Engineering,
Vol. 253,
Issue. ,
p.
111247.
Guvernyuk, S. V.
Dynnikov, Ya. A.
Dynnikova, G. Ya.
and
Malakhova, T. V.
2022.
Hydrodynamic Mechanisms of the Influence of an Elastic Constraint on the Propulsive Force of Airfoil under Semideterministic Oscillations in Viscous Fluid Flow.
Fluid Dynamics,
Vol. 57,
Issue. 5,
p.
549.
Zhang, Chengyao
Zhao, Zhiye
Huang, Haibo
Lv, Xingbing
Lu, Xi-Yun
and
Yu, Peng
2022.
Effect of non-uniform stiffness distribution on the dynamics of inverted plates in a uniform flow.
Physics of Fluids,
Vol. 34,
Issue. 11,
Xu, Chang
Liu, Xuechao
Liu, Kui
Xiong, Yongfeng
and
Huang, Haibo
2022.
A free flexible flap in channel flow.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Wu, Buchen
Shu, Chang
Lee, HsuChew
and
Wan, Minping
2022.
The effects of caudal fin's bending stiffness on a self-propelled carangiform swimmer.
Physics of Fluids,
Vol. 34,
Issue. 4,
Liu, Yanwen
and
Jiang, Hongzhou
2022.
Research Development on Fish Swimming.
Chinese Journal of Mechanical Engineering,
Vol. 35,
Issue. 1,
Liu, Kui
Liu, Xuechao
and
Huang, Haibo
2022.
Scaling the self-propulsive performance of pitching and heaving flexible plates.
Journal of Fluid Mechanics,
Vol. 936,
Issue. ,
Wu, Buchen
Shu, Chang
Wan, Minping
Wang, Yan
and
Chen, Shiyi
2022.
Hydrodynamic performance of an unconstrained flapping swimmer with flexible fin: A numerical study.
Physics of Fluids,
Vol. 34,
Issue. 1,
Wang, Chenglei
Tang, Hui
and
Zhang, Xing
2022.
Fluid-structure interaction of bio-inspired flexible slender structures: a review of selected topics.
Bioinspiration & Biomimetics,
Vol. 17,
Issue. 4,
p.
041002.
Zhang, Dong
Zhang, Jun-Duo
and
Huang, Wei-Xi
2022.
Physical models and vortex dynamics of swimming and flying: a review.
Acta Mechanica,
Vol. 233,
Issue. 4,
p.
1249.
Lee, Minseop
Jung, Cheolgyun
Lee, Jeongsu
and
Kim, Daegyoum
2023.
Gravity-coupled flutter and contact of a flag near a wall.
Journal of Fluid Mechanics,
Vol. 977,
Issue. ,
Xue, Jiaqi
Han, Fei
Klaassen van Oorschot, Brett
Clifton, Glenna
and
Fan, Dixia
2023.
Exploring storm petrel pattering and sea-anchoring using deep reinforcement learning.
Bioinspiration & Biomimetics,
Vol. 18,
Issue. 6,
p.
066016.
Luo, Xian-Guang
Gao, An-Kang
and
Lu, Xi-Yun
2023.
Enhanced performance of a self-propelled flexible plate by a uniform shear flow and mechanism insight.
Physics of Fluids,
Vol. 35,
Issue. 2,
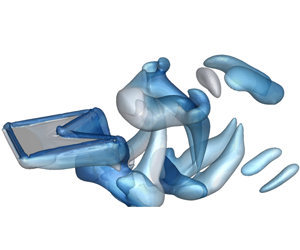
 $\unicode[STIX]{x1D719}$ varies from
$\unicode[STIX]{x1D719}$ varies from  $30^{\circ }$ (concave plate) to
$30^{\circ }$ (concave plate) to  $150^{\circ }$ (convex plate). Under different bending stiffnesses
$150^{\circ }$ (convex plate). Under different bending stiffnesses  $K$, three regimes of the propulsive performance in terms of propulsive velocity
$K$, three regimes of the propulsive performance in terms of propulsive velocity  $U$ and efficiency
$U$ and efficiency  $\unicode[STIX]{x1D702}$ as a function of
$\unicode[STIX]{x1D702}$ as a function of  $\unicode[STIX]{x1D719}$ are identified. When
$\unicode[STIX]{x1D719}$ are identified. When  $K$ is small, moderate and large, the square, convex and concave plate achieves the best performance, respectively. Analyses of vortical structures and velocity fields show that usually the jet behind the plate with the best performance is longest. Besides, the inclination angle of the jet may be small. The different propulsive performances at small and moderate
$K$ is small, moderate and large, the square, convex and concave plate achieves the best performance, respectively. Analyses of vortical structures and velocity fields show that usually the jet behind the plate with the best performance is longest. Besides, the inclination angle of the jet may be small. The different propulsive performances at small and moderate  $K$ are mainly attributed to the phase lag of the trailing edge. The force acting on the plate is analysed and it is found that the thrust force is mainly contributed by the normal force. If
$K$ are mainly attributed to the phase lag of the trailing edge. The force acting on the plate is analysed and it is found that the thrust force is mainly contributed by the normal force. If  $U$,
$U$,  $\unicode[STIX]{x1D702}$ and
$\unicode[STIX]{x1D702}$ and  $K$ are rescaled by the normal force and the area moment of the plate, the curves for different
$K$ are rescaled by the normal force and the area moment of the plate, the curves for different  $\unicode[STIX]{x1D719}$ almost collapse into a single curve when the bending stiffness coefficient is small or moderate. The scaling confirms that the normal force should be the characteristic fluid force at small or moderate
$\unicode[STIX]{x1D719}$ almost collapse into a single curve when the bending stiffness coefficient is small or moderate. The scaling confirms that the normal force should be the characteristic fluid force at small or moderate  $K$ and the
$K$ and the  $\unicode[STIX]{x1D719}$ effect is governed by the area moment. The findings may shed some light on the propulsive performance of aquatic animals.
$\unicode[STIX]{x1D719}$ effect is governed by the area moment. The findings may shed some light on the propulsive performance of aquatic animals.