Published online by Cambridge University Press: 16 March 2017
Detonation propagation in the limit of highly spatially discretized energy sources is investigated. The model of this problem begins with a medium consisting of a calorically perfect gas with a prescribed energy release per unit mass. The energy release is collected into sheet-like sources that are embedded in an inert gas that fills the spaces between them. The release of energy in the first sheet results in a planar blast wave that propagates to the next source, which is triggered after a prescribed delay, generating a new blast, and so forth. The resulting wave dynamics as the front passes through hundreds of such sources is computationally simulated by numerically solving the governing one-dimensional Euler equations in the laboratory-fixed reference frame. Two different solvers are used: one with a fixed uniform grid and the other using an unstructured, adaptively refined grid enabling the limit of highly concentrated, spatially discrete sources to be examined. The two different solvers generate consistent results, agreeing within the accuracy of the measured wave speeds. The average wave speed for each simulation is measured once the wave propagation has reached a quasi-periodic solution. The effect of source delay time, source energy density, specific heat ratio and the spatial discreteness of the sources on the wave speed is studied. Sources fixed in the laboratory reference frame versus sources that convect with the flow are compared. Simulations using an Arrhenius-rate-dependent energy release are performed as well. The average wave speed is compared to the ideal Chapman–Jouguet (CJ) speed of the equivalent homogenized media. Velocities in excess of the CJ speed are found as the sources are made increasingly discrete, with the deviation above CJ being as great as 15 %. The deviation above the CJ value increases with decreasing values of specific heat ratio
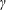 $\unicode[STIX]{x1D6FE}$
. The total energy release, delay time and whether the sources remain laboratory-fixed or are convected with the flow do not have a significant influence on the deviation of the average wave speed away from CJ. A simple, ad hoc analytic model is proposed to treat the case of zero delay time (i.e. source energy released at the shock front) that exhibits qualitative agreement with the computational solutions and may explain why the deviation from CJ increases with decreasing
$\unicode[STIX]{x1D6FE}$
. The total energy release, delay time and whether the sources remain laboratory-fixed or are convected with the flow do not have a significant influence on the deviation of the average wave speed away from CJ. A simple, ad hoc analytic model is proposed to treat the case of zero delay time (i.e. source energy released at the shock front) that exhibits qualitative agreement with the computational solutions and may explain why the deviation from CJ increases with decreasing
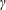 $\unicode[STIX]{x1D6FE}$
. When the sources are sufficiently spread out so as to make the energy release of the media nearly continuous, the classic CJ solution is obtained for the average wave speed. Such continuous waves can also be shown to have a time-averaged structure consistent with the classical Zel’dovich–von Neumann–Döring (ZND) structure of a detonation. In the limit of highly discrete sources, temporal averaging of the wave structure shows that the effective sonic surface does not correspond to an equilibrium state. The average state of the flow leaving the wave in this case does eventually reach the equilibrium Hugoniot, but only after the effective sonic surface has been crossed. Thus, the super-CJ waves observed in the limit of highly discretized sources can be understood as weak detonations due to the non-equilibrium state at the effective sonic surface. These results have implications for the validity of the CJ criterion as applied to highly unstable detonations in gases and heterogeneous detonations in condensed phase and multiphase media.
$\unicode[STIX]{x1D6FE}$
. When the sources are sufficiently spread out so as to make the energy release of the media nearly continuous, the classic CJ solution is obtained for the average wave speed. Such continuous waves can also be shown to have a time-averaged structure consistent with the classical Zel’dovich–von Neumann–Döring (ZND) structure of a detonation. In the limit of highly discrete sources, temporal averaging of the wave structure shows that the effective sonic surface does not correspond to an equilibrium state. The average state of the flow leaving the wave in this case does eventually reach the equilibrium Hugoniot, but only after the effective sonic surface has been crossed. Thus, the super-CJ waves observed in the limit of highly discretized sources can be understood as weak detonations due to the non-equilibrium state at the effective sonic surface. These results have implications for the validity of the CJ criterion as applied to highly unstable detonations in gases and heterogeneous detonations in condensed phase and multiphase media.