Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2025-01-06T03:22:28.788Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of slip and surface texture on turbulence over superhydrophobic surfaces

Published online by Cambridge University Press:  19 December 2018

C. T. Fairhall Open the ORCID record for C. T. Fairhall [Opens in a new window] ,
N. Abderrahaman-Elena Open the ORCID record for N. Abderrahaman-Elena [Opens in a new window]  and
R. García-Mayoral Open the ORCID record for R. García-Mayoral [Opens in a new window]
C. T. Fairhall
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
N. Abderrahaman-Elena
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
R. García-Mayoral*
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Superhydrophobic surfaces are able to entrap gas pockets in between surface roughness elements when submerged in water. These entrapped gas pockets give these surfaces the potential to reduce drag due to the overlying flow being able to locally slip over the gas pockets, resulting in a mean slip at the surface. In this work we assess the separate effects that surface slip and surface texture have on turbulence over superhydrophobic surfaces. We show that the direct effect of surface slip does not modify the dynamics of the overlying turbulence, which remains canonical or smooth-wall like. The surface drag is governed by the difference between two virtual origins, the virtual origin of the mean flow and the virtual origin experienced by the overlying turbulence, in an extension of the theory from Luchini, Manzo & Pozzi (J. Fluid Mech., vol. 228, 1991, pp. 87–109) for riblets. Streamwise slip deepens the virtual origin of the mean flow, while spanwise slip deepens the virtual origin perceived by the overlying turbulence. Drag reduction is then proportional to the difference between the two virtual origins. We decompose the near-wall flow into background-turbulence and texture-coherent components, and show that the background-turbulence component experiences the surface as homogeneous slip lengths. 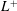The validity of the slip-length model can then be extended to larger texture size $L^{+}$ than thought in previous studies. For 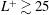$L^{+}\gtrsim 25$, however, we observe that a nonlinear interaction with the texture-coherent flow develops that alters the dynamics of the background turbulence, exhibiting a modified distribution of turbulent energy across length scales. This has the effect of reducing the velocity increment 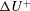$\unicode[STIX]{x0394}U^{+}$ compared to that predicted using homogeneous slip lengths and sets the upper limit of applicability of slip-length models.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 88 - 118
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abderrahaman-Elena, N., Fairhall, C. T. & García-Mayoral, R.2019 Roughness induced modulation of near-wall turbulence in the transitionally rough regime. arXiv:1808.10825.Google Scholar
Abderrahaman-Elena, N. & García-Mayoral, R. 2016 Geometry-induced fluctuations in the transitionally rough regime. J. Phys. Conf. Ser. 708, 012009.Google Scholar
Antonia, R. A. & Krogstad, P.-A. 2001 Turbulence structure in boundary layers over different types of surface roughness. Fluid Dyn. Res. 28, 139–157.Google Scholar
Bechert, D. W. & Bartenwerfer, M. 1989 The viscous flow on surfaces with longitudinal ribs. J. Fluid Mech. 206, 105–129.Google Scholar
Bechert, D. W., Bruse, M., Hage, W., van der Hoeven, J. G. T. & Hoppe, G. 1997 Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 338, 59–87.Google Scholar
Bidkar, R. A., Leblanc, L., Kulkarni, A. J., Bahadur, V., Ceccio, S. L. & Perlin, M. 2014 Skin-friction drag reduction in the turbulent regime using random-textured hydrophobic surfaces. Phys. Fluids 26, 085108.Google Scholar
Blackwelder, R. F. & Eckelmann, H. 1979 Streamwise vortices associated with the bursting phenomenon. J. Fluid Mech. 94, 577–594.Google Scholar
Busse, A. & Sandham, N. D. 2012 Influence of an anisotropic slip-length boundary condition on turbulent channel flow. Phys. Fluids 24, 055111.Google Scholar
Busse, A. & Sandham, N. D. 2013 Turbulent flow over superhydrophobic surfaces – roughness versus slip. In Proceedings of the 14th European Turbulence Conference Lyon, France.Google Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51.Google Scholar
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P. 2009 Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 21, 085103.Google Scholar
Fairhall, C. T. & García-Mayoral, R. 2018 Spectral analysis of the slip-length model for turbulence over textured superhydrophobic surfaces. Flow Turbul. Combust. 100, 961–978.Google Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18, 051703.Google Scholar
García-Mayoral, R., Gómez-de-Segura, G. & Fairhall, C. T. 2018 The control of near-wall turbulence through surface texturing. Fluid Dyn. Res. https://doi.org/10.1088/1873-7005/aadfcc.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.Google Scholar
Gatti, D. & Quadrio, M. 2016 Reynolds-number dependence of turbulent skin-friction drag reduction induced by spanwise forcing. J. Fluid Mech. 802, 553–582.Google Scholar
Gómez-de-Segura, G., Fairhall, C. T., MacDonald, M., Chung, D. & García-Mayoral, R. 2018 Manipulation of near-wall turbulence by surface slip and permeability. J. Phys. Conf. Ser. 1001, 012011.Google Scholar
Gose, J. W., Golovin, K., Boban, M., Mabry, J. M., Tuteja, A., Perlin, M. & Ceccio, S. L. 2018 Characterization of superhydrophobic surfaces for drag reduction in turbulent flow. J. Fluid Mech. 845, 560–580.Google Scholar
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26, 095102.Google Scholar
Jiménez, J. 1994 On the structure and control of near wall turbulence. Phys. Fluids 6, 944–953.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.Google Scholar
Krogstad, P.-A. & Antonia, R. A. 1994 Structure of turbulent boundary layers on smooth and rough walls. J. Fluid Mech. 277, 1–21.Google Scholar
Lafuma, A. & Quere, D. 2011 Slippery pre-suffused surfaces. Europhys. Lett. 96, 56001.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Le, H. & Moin, P. 1991 An improvement of fractional step methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 92, 369–379.Google Scholar
Ling, H., Srinivasan, S., Golovin, K., McKinley, G. H., Tuteja, A. & Katz, J. 2016 High-resolution velocity measurements in the inner part of turbulent boundary layers over super-hydrophobic surfaces. J. Fluid Mech. 801, 670–703.Google Scholar
Luchini, P. 1996 Reducing the turbulent skin friction. In Computational Methods in Applied Sciences – Proceedings of the 3rd ECCOMAS CFD Conference, pp. 466–470. Wiley.Google Scholar
Luchini, P. 2015 The relevance of longitudinal and transverse protrusion heights for drag reduction by a superhydrophobic surface. In Proceedings of the European Drag Reduction and Flow Control Meeting 2015, Cambridge, UK, pp. 81–82.Google Scholar
Luchini, P., Manzo, F. & Pozzi, A. 1991 Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2010 An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation. Phys. Fluids 22, 065102.Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16, L55–L58.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Navier, C. L. M. H. 1823 Memoire sur les lois du mouvement des fluide. Mem. Acad. R. Sci. Inst. France 6, 389–440.Google Scholar
Orlandi, P. & Leonardi, S. 2006 DNS of turbulent channel flows with two- and three-dimensional roughness. J. Turbul. 7, N73.Google Scholar
Ou, J., Perot, B. & Rothstein, J. P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635–4643.Google Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.Google Scholar
Philip, J. R. 1972 Flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23, 353–372.Google Scholar
Rastegari, A. & Akhavan, R. 2015 On the mechanism of turbulent drag reduction with super-hydrophobic surfaces. J. Fluid Mech. 773, R4.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54, 263–288.Google Scholar
Rosenberg, B. J., Buren, T. V., Fu, M. K. & Smits, A. J. 2016 Turbulent drag reduction over air- and liquid-impregnated surfaces. Phys. Fluids 28, 015103.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Schonecker, C., Baier, T. & Hardt, S. 2014 Influence of the enclosed fluid on the flow over a microstructured surface in the Cassie state. J. Fluid Mech. 740, 168–195.Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2015 Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 783, 448–473.Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2018 Turbulent flows over superhydrophobic surfaces: flow-induced capillary waves, and robustness of air-water interfaces. J. Fluid Mech. 835, 45–85.Google Scholar
Seo, J. & Mani, A. 2016 On the scaling of the slip velocity in turbulent flows over superhydrophobic surfaces. Phys. Fluids 28, 025110.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to Re 𝜃 = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Türk, S., Daschiel, G., Stroh, A., Hasegawa, Y. & Frohnapfel, B. 2014 Turbulent flow over superhydrophobic surfaces with streamwise grooves. J. Fluid Mech. 747, 186–217.Google Scholar
Watanabe, K., Udagawa, Y. & Udagawa, H. 1999 Drag reduction of Newtonian fluid in a circular pipe with a highly water-repellent wall. J. Fluid Mech. 381, 225–238.Google Scholar
Wexler, J. S., Grosskopf, A., Chow, M., Fan, Y., Jacobi, I. & Stone, H. A. 2015a Robust liquid-infused surfaces through patterned wettability. Soft Matt. 11, 5023–5029.Google Scholar
Wexler, J. S., Jacobi, I. & Stone, H. A. 2015b Shear-driven failure of liquid-infused surfaces. Phys. Rev. Let. 114, 168301.Google Scholar
Wong, T.-S., Kang, S. H., Tang, S. K. Y., Smythe, E. J., Hatton, B. D., Grinthal, A. & Aizenberg, J. 2011 Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 477, 443–447.Google Scholar
Woolford, B., Prince, J., Maynes, D. & Webb, B. W. 2009 Particle image velocimetry characterization of turbulent channel flow with rib patterned superhydrophobic walls. Phys. Fluids 21, 085106.Google Scholar
Ybert, C., Barentin, C. & Cottin-Bizonne, C. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19, 123601.Google Scholar