Article contents
The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects
Published online by Cambridge University Press: 11 May 2016
Abstract
In this study, we analyse the statistics of both individual inertial particles and inertial particle pairs in direct numerical simulations of homogeneous isotropic turbulence in the absence of gravity. The effect of the Taylor microscale Reynolds number, 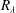 $R_{{\it\lambda}}$, on the particle statistics is examined over the largest range to date (from
$R_{{\it\lambda}}$, on the particle statistics is examined over the largest range to date (from 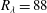 $R_{{\it\lambda}}=88$ to 597), at small, intermediate and large Kolmogorov-scale Stokes numbers
$R_{{\it\lambda}}=88$ to 597), at small, intermediate and large Kolmogorov-scale Stokes numbers 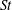 $St$. We first explore the effect of preferential sampling on the single-particle statistics and find that low-
$St$. We first explore the effect of preferential sampling on the single-particle statistics and find that low-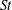 $St$ inertial particles are ejected from both vortex tubes and vortex sheets (the latter becoming increasingly prevalent at higher Reynolds numbers) and preferentially accumulate in regions of irrotational dissipation. We use this understanding of preferential sampling to provide a physical explanation for many of the trends in the particle velocity gradients, kinetic energies and accelerations at low
$St$ inertial particles are ejected from both vortex tubes and vortex sheets (the latter becoming increasingly prevalent at higher Reynolds numbers) and preferentially accumulate in regions of irrotational dissipation. We use this understanding of preferential sampling to provide a physical explanation for many of the trends in the particle velocity gradients, kinetic energies and accelerations at low 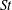 $St$, which are well represented by the model of Chun et al. (J. Fluid Mech., vol. 536, 2005, pp. 219–251). As
$St$, which are well represented by the model of Chun et al. (J. Fluid Mech., vol. 536, 2005, pp. 219–251). As 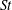 $St$ increases, inertial filtering effects become more important, causing the particle kinetic energies and accelerations to decrease. The effect of inertial filtering on the particle kinetic energies and accelerations diminishes with increasing Reynolds number and is well captured by the models of Abrahamson (Chem. Engng Sci., vol. 30, 1975, pp. 1371–1379) and Zaichik & Alipchenkov (Intl J. Multiphase Flow, vol. 34 (9), 2008, pp. 865–868), respectively. We then consider particle-pair statistics, and focus our attention on the relative velocities and radial distribution functions (RDFs) of the particles, with the aim of understanding the underlying physical mechanisms contributing to particle collisions. The relative velocity statistics indicate that preferential sampling effects are important for
$St$ increases, inertial filtering effects become more important, causing the particle kinetic energies and accelerations to decrease. The effect of inertial filtering on the particle kinetic energies and accelerations diminishes with increasing Reynolds number and is well captured by the models of Abrahamson (Chem. Engng Sci., vol. 30, 1975, pp. 1371–1379) and Zaichik & Alipchenkov (Intl J. Multiphase Flow, vol. 34 (9), 2008, pp. 865–868), respectively. We then consider particle-pair statistics, and focus our attention on the relative velocities and radial distribution functions (RDFs) of the particles, with the aim of understanding the underlying physical mechanisms contributing to particle collisions. The relative velocity statistics indicate that preferential sampling effects are important for 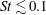 $St\lesssim 0.1$ and that path-history/non-local effects become increasingly important for
$St\lesssim 0.1$ and that path-history/non-local effects become increasingly important for 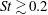 $St\gtrsim 0.2$. While higher-order relative velocity statistics are influenced by the increased intermittency of the turbulence at high Reynolds numbers, the lower-order relative velocity statistics are only weakly sensitive to changes in Reynolds number at low
$St\gtrsim 0.2$. While higher-order relative velocity statistics are influenced by the increased intermittency of the turbulence at high Reynolds numbers, the lower-order relative velocity statistics are only weakly sensitive to changes in Reynolds number at low 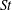 $St$. The Reynolds-number trends in these quantities at intermediate and large
$St$. The Reynolds-number trends in these quantities at intermediate and large 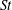 $St$ are explained based on the influence of the available flow scales on the path-history and inertial filtering effects. We find that the RDFs peak near
$St$ are explained based on the influence of the available flow scales on the path-history and inertial filtering effects. We find that the RDFs peak near 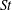 $St$ of order unity, that they exhibit power-law scaling for low and intermediate
$St$ of order unity, that they exhibit power-law scaling for low and intermediate 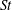 $St$ and that they are largely independent of Reynolds number for low and intermediate
$St$ and that they are largely independent of Reynolds number for low and intermediate 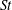 $St$. We use the model of Zaichik & Alipchenkov (New J. Phys., vol. 11, 2009, 103018) to explain the physical mechanisms responsible for these trends, and find that this model is able to capture the quantitative behaviour of the RDFs extremely well when direct numerical simulation data for the structure functions are specified, in agreement with Bragg & Collins (New J. Phys., vol. 16, 2014a, 055013). We also observe that at large
$St$. We use the model of Zaichik & Alipchenkov (New J. Phys., vol. 11, 2009, 103018) to explain the physical mechanisms responsible for these trends, and find that this model is able to capture the quantitative behaviour of the RDFs extremely well when direct numerical simulation data for the structure functions are specified, in agreement with Bragg & Collins (New J. Phys., vol. 16, 2014a, 055013). We also observe that at large 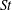 $St$, changes in the RDF are related to changes in the scaling exponents of the relative velocity variances. The particle collision kernel closely matches that computed by Rosa et al. (New J. Phys., vol. 15, 2013, 045032) and is found to be largely insensitive to the flow Reynolds number. This suggests that relatively low-Reynolds-number simulations may be able to capture much of the relevant physics of droplet collisions and growth in the adiabatic cores of atmospheric clouds.
$St$, changes in the RDF are related to changes in the scaling exponents of the relative velocity variances. The particle collision kernel closely matches that computed by Rosa et al. (New J. Phys., vol. 15, 2013, 045032) and is found to be largely insensitive to the flow Reynolds number. This suggests that relatively low-Reynolds-number simulations may be able to capture much of the relevant physics of droplet collisions and growth in the adiabatic cores of atmospheric clouds.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
Footnotes
Present address: Applied Mathematics and Plasma Physics Group, Los Alamos National Laboratory, Los Alamos, NM 87545, USA.
References
- 115
- Cited by



