Article contents
The effect of heat release on the entrainment in a turbulent mixing layer
Published online by Cambridge University Press: 03 April 2018
Abstract
Direct numerical simulations of a temporally evolving compressible reacting mixing layer have been performed to study the entrainment of the irrotational flow into the turbulent region across the turbulent/non-turbulent interface (TNTI). In order to study the effects of heat release and interaction of the flame with the TNTI on turbulence several cases with different heat release levels, 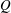 $Q$, and stoichiometric mixture fractions are chosen for the simulations with the highest opted value for
$Q$, and stoichiometric mixture fractions are chosen for the simulations with the highest opted value for 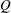 $Q$ corresponding to hydrogen combustion in air. The combustion is mimicked by a one-step irreversible global reaction, and infinitely fast chemistry approximation is used to compute the species mass fractions. Entrainment is studied via two mechanisms: nibbling, considered as the vorticity transport across the TNTI, and engulfment, the drawing of the pockets of the outside irrotational fluid into the turbulent region. As the level of heat release increases, the total entrained mass flow rate into the mixing layer decreases. In a reacting mixing layer by increasing the heat release rate, the mass flow rate due to nibbling is shown to decrease mostly due to a reduction of the local entrainment velocity, while the surface area of the TNTI does not change significantly. It is also observed that nibbling is a viscous dominated mechanism in non-reacting flows, whereas it is mostly carried out by inviscid terms in reacting flows with high level of heat release. The contribution of the engulfment to entrainment is small for the non-reacting mixing layers, while mass flow rate due to engulfment can constitute close to 40 % of the total entrainment in reacting cases. This increase is primarily related to a decrease of entrained mass flow rate due to nibbling, while the entrained mass flow rate due to engulfment does not change significantly in reacting cases. It is shown that the total entrained mass flow rate in reacting and non-reacting compressible mixing layers can be estimated from an expression containing the convective Mach number and the density change due to heat release.
$Q$ corresponding to hydrogen combustion in air. The combustion is mimicked by a one-step irreversible global reaction, and infinitely fast chemistry approximation is used to compute the species mass fractions. Entrainment is studied via two mechanisms: nibbling, considered as the vorticity transport across the TNTI, and engulfment, the drawing of the pockets of the outside irrotational fluid into the turbulent region. As the level of heat release increases, the total entrained mass flow rate into the mixing layer decreases. In a reacting mixing layer by increasing the heat release rate, the mass flow rate due to nibbling is shown to decrease mostly due to a reduction of the local entrainment velocity, while the surface area of the TNTI does not change significantly. It is also observed that nibbling is a viscous dominated mechanism in non-reacting flows, whereas it is mostly carried out by inviscid terms in reacting flows with high level of heat release. The contribution of the engulfment to entrainment is small for the non-reacting mixing layers, while mass flow rate due to engulfment can constitute close to 40 % of the total entrainment in reacting cases. This increase is primarily related to a decrease of entrained mass flow rate due to nibbling, while the entrained mass flow rate due to engulfment does not change significantly in reacting cases. It is shown that the total entrained mass flow rate in reacting and non-reacting compressible mixing layers can be estimated from an expression containing the convective Mach number and the density change due to heat release.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
Present address: Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218-2682, USA.
References
Jahanbakhshi et al. supplementary movie 1
In this movie a 3D view of the DNS data during the self-similar stage is shown. The gray surfaces are isosurfaces of a positive value of discriminant of velocity gradient tensor representing the vortical structures in the flow and the red surface is the flame.
Jahanbakhshi et al. supplementary movie 2
This movie is a streamwise cut through of the shear layer viewed from the lower stream. The gray surfaces are isosurfaces of a positive value of discriminant of velocity gradient tensor, the red surface is the flame, and the orange translucent surfaces are the TNTIs.
- 29
- Cited by


