Article contents
Early spray development at high gas density: hole, ligament and bridge formations
Published online by Cambridge University Press: 01 March 2016
Abstract
Three-dimensional temporal instabilities, leading to spray formation of a round liquid jet segment with an outer, coaxial high-density gas flow, are studied with Navier–Stokes and level-set computations. These computations predict the liquid surface shape showing the smaller structures on the conical wave crests, i.e. lobes, holes, bridges and ligaments, which are the precursors to droplet and spray formations. These structures and their time scales affect droplet size and velocity distributions as well as spray cone angles. The gas-to-liquid density ratio, liquid Reynolds number (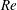 $Re$) and liquid Weber number (
$Re$) and liquid Weber number (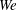 $We$) range between 0.02–0.9, 320–16 000 and 2000–230 000, respectively, which cover three distinct physical domains. (1) At higher
$We$) range between 0.02–0.9, 320–16 000 and 2000–230 000, respectively, which cover three distinct physical domains. (1) At higher 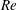 $Re$ and
$Re$ and 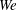 $We$, ligaments and then drops develop following hole and liquid bridge formations. (2) At higher gas densities throughout the
$We$, ligaments and then drops develop following hole and liquid bridge formations. (2) At higher gas densities throughout the 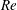 $Re$ range, several holes merge forming two bridges per lobe before breaking to form ligaments; this hole merging is explained by slower development of hairpin vortices and lobe shape. (3) In cases where both gas density and
$Re$ range, several holes merge forming two bridges per lobe before breaking to form ligaments; this hole merging is explained by slower development of hairpin vortices and lobe shape. (3) In cases where both gas density and 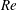 $Re$ or
$Re$ or 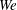 $We$ are lower, the well-ordered lobes are replaced by more irregular, smaller-scale corrugations along the conical wave crest edge; ligaments form differently by stretching from the lobes before holes form. Thicker ligaments and larger droplets form in the low
$We$ are lower, the well-ordered lobes are replaced by more irregular, smaller-scale corrugations along the conical wave crest edge; ligaments form differently by stretching from the lobes before holes form. Thicker ligaments and larger droplets form in the low 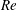 $Re$, low gas density range. The surface wave dynamics, vortex dynamics and their interactions are explained. Understandings of liquid stream break up and concurrent smaller structure formation are built upon an examination of both translation and rotation of the fluid. In all cases, hole formation is correlated with hairpin and helical vortices; fluid motion through a perforation in the thin sheet near the wave crest corresponds to these vortices. The hole formation process is dominated by inertial forces rather than capillary action, which differs from mechanisms suggested previously for other configurations. Circulation due to streamwise vorticity increases while the lobes thin and holes form. For larger surface tension, cavities in the jet core rather than perforations in a sheet occur. The more rapid radial extension of the two-phase mixture with increasing gas density is explained by greater circulation in the ring (i.e. wave crest) region. Experimental descriptions of the smaller structures are available only at lower
$Re$, low gas density range. The surface wave dynamics, vortex dynamics and their interactions are explained. Understandings of liquid stream break up and concurrent smaller structure formation are built upon an examination of both translation and rotation of the fluid. In all cases, hole formation is correlated with hairpin and helical vortices; fluid motion through a perforation in the thin sheet near the wave crest corresponds to these vortices. The hole formation process is dominated by inertial forces rather than capillary action, which differs from mechanisms suggested previously for other configurations. Circulation due to streamwise vorticity increases while the lobes thin and holes form. For larger surface tension, cavities in the jet core rather than perforations in a sheet occur. The more rapid radial extension of the two-phase mixture with increasing gas density is explained by greater circulation in the ring (i.e. wave crest) region. Experimental descriptions of the smaller structures are available only at lower 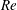 $Re$ and lower density, agreeing with the computations. Computed scales of bridges, ligaments, early droplets and emerging spray radii agree qualitatively with experimental evidence through the high
$Re$ and lower density, agreeing with the computations. Computed scales of bridges, ligaments, early droplets and emerging spray radii agree qualitatively with experimental evidence through the high 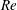 $Re$ and
$Re$ and 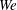 $We$ domains.
$We$ domains.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 49
- Cited by



