Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T01:53:10.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection with modulated rotation

Published online by Cambridge University Press:  04 August 2015

Jin-Qiang Zhong ,
Sebastian Sterl  and
Hui-Min Li
Jin-Qiang Zhong*
Affiliation:
Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology and School of Physics Science and Engineering, Tongji University, Shanghai 200092, China
Sebastian Sterl
Affiliation:
Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology and School of Physics Science and Engineering, Tongji University, Shanghai 200092, China Physics of Fluids Group, Faculty of Science and Technology, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Hui-Min Li
Affiliation:
Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology and School of Physics Science and Engineering, Tongji University, Shanghai 200092, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present measurements of the azimuthal rotation velocity 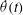$\dot{{\it\theta}}(t)$ and thermal amplitude 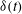${\it\delta}(t)$ of the large-scale circulation in turbulent Rayleigh–Bénard convection with modulated rotation. Both 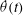$\dot{{\it\theta}}(t)$ and 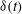${\it\delta}(t)$ exhibit clear oscillations at the modulation frequency 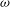${\it\omega}$. Fluid acceleration driven by oscillating Coriolis force causes an increasing phase lag in 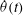$\dot{{\it\theta}}(t)$ when 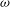${\it\omega}$ increases. The applied modulation produces oscillatory boundary layers and the resulting time-varying viscous drag modifies 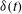${\it\delta}(t)$ periodically. Oscillation of 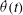$\dot{{\it\theta}}(t)$ with maximum amplitude occurs at a finite modulation frequency 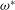${\it\omega}^{\ast }$. Such a resonance-like phenomenon is interpreted as a result of optimal coupling of 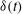${\it\delta}(t)$ to the modulated rotation velocity. We show that an extended large-scale circulation model with a relaxation time for 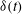${\it\delta}(t)$ in response to the modulated rotation provides predictions in close agreement with the experimental results.

JFM classification

Geophysical and Geological Flows: Rotating flows Turbulent Flows: Turbulent convection
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , R4
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Araujo, F. F., Grossmann, S. & Lohse, D. 2005 Wind reversals in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084502.CrossRefGoogle ScholarPubMed
Assaf, M., Angheluta, L. & Goldenfeld, N. 2012 Effect of weak rotation on large-scale circulation cessations in turbulent convection. Phys. Rev. Lett. 109, 074502.CrossRefGoogle ScholarPubMed
Avila, M., Belisle, M. J., Lopez, J. M., Marques, F. & Saric, W. S. 2008 Mode competition in modulated Taylor–Couette flow. J. Fluid Mech. 601, 381–406.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006 Effect of the Earth’s coriolis force on the large-scale circulation of turbulent Rayleigh–Bénard convection. Phys. Fluids 18, 125108.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.CrossRefGoogle ScholarPubMed
Brown, E. & Ahlers, G. 2008 A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 075101.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
Busse, F. H. 2000 Homogeneous dynamos in planetary cores and in the laboratory. Annu. Rev. Fluid Mech. 32, 383–408.CrossRefGoogle Scholar
Chillá, A. F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 1–25.CrossRefGoogle ScholarPubMed
Doake, C. S. M. 1977 Possible effect of ice ages on Earth’s magnetic field. Nature 267, 415–417.CrossRefGoogle Scholar
Donnelly, R. J. 1964 Experiments on the stability of viscous flow between rotating cylinders. III. Enhancement of stability by modulation. Proc. R. Soc. Lond. A 281, 130–139.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.CrossRefGoogle Scholar
Geurts, B. J. & Kunnen, R. P. J. 2014 Intensified heat transfer in modulated rotating Rayleigh–Bénard convection. Intl J. Heat Fluid Flow 49, 62–68.CrossRefGoogle Scholar
Hall, P. 1975 The stability of unsteady cylinder flows. J. Fluid Mech. 67, 29–63.CrossRefGoogle Scholar
Hart, J. E., Kittelman, S. & Ohlsen, D. R. 2002 Mean flow precession and temperature probability density functions in turbulent rotating convection. Phys. Fluids 14, 955–962.CrossRefGoogle Scholar
Koning, A. & Dumberry, M. 2013 Internal forcing of Mercury’s long period free librations. Icarus 223, 40–47.CrossRefGoogle Scholar
Krishnamurti, R. & Howard, L. N. 1981 Large scale flow generation in turbulent convection. Proc. Natl Acad. Sci. USA 78, 1981–1985.CrossRefGoogle ScholarPubMed
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008 Breakdown of large-scale circulation in turbulent rotating convection. Eur. Phys. Lett. 84, 24001.CrossRefGoogle Scholar
Kunnen, R. P. J., Stevens, R. J. A. M., Overkamp, J., Sun, C., van Heijst, G. F. & Clercx, H. J. H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory and models. Rev. Geophys. 37, 1–64.CrossRefGoogle Scholar
Miesch, M. S. 2000 The coupling of solar convection and rotation. Solar Phys. 192, 59–89.CrossRefGoogle Scholar
Miyagoshi, T. & Hamano, Y. 2013 Magnetic field variation caused by rotational speed change in a magnetohydrodynamic dynamo. Phys. Rev. Lett. 111, 124501.CrossRefGoogle Scholar
Niemela, J. J., Babuin, S. & Sreenivasan, K. R. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.CrossRefGoogle Scholar
Niemela, J. J., Babuin, S. & Sreenivasan, K. R. 2010 Turbulent rotating convection at high Rayleigh and Taylor numbers. J. Fluid Mech. 649, 509–522.CrossRefGoogle Scholar
Niemela, J. J., Smith, M. R. & Donnelly, R. J. 1991 Convective instability with time-varying rotation. Phys. Rev. A 44, 8406–8409.CrossRefGoogle ScholarPubMed
Olson, P. 2013 Experimental dynamos and the dynamics of planetary cores. Annu. Rev. Earth Planet. Sci. 41, 153–181.CrossRefGoogle Scholar
Resagk, C., du Puits, R., Thess, A., Dolzhansky, F. V., Grossmann, S., Araujo, F. F. & Lohse, D. 2006 Oscillations of the large scale wind in turbulent thermal convection. Phys. Fluids 18, 095105.CrossRefGoogle Scholar
Song, H., Brown, E., Hawkins, R. & Tong, P. 2014 Dynamics of large-scale circulation of turbulent thermal convection in a horizontal cylinder. J. Fluid Mech. 740, 136–167.CrossRefGoogle Scholar
Sreenivasan, K. R., Bershadskii, A. & Niemela, J. J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65, 056306.CrossRefGoogle ScholarPubMed
Thompson, K. L., Bajaj, K. M. S. & Ahlers, G. 2002 Traveling concentric-roll patterns in Rayleigh–Bénard convection with modulated rotation. Phys. Rev. E 65, 046218.CrossRefGoogle ScholarPubMed
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.CrossRefGoogle ScholarPubMed
Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.CrossRefGoogle Scholar
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google ScholarPubMed