Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T15:10:34.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of m = 0 and m = 1 modes and of streamwise vortices in a turbulent axisymmetric mixing layer

Published online by Cambridge University Press:  13 September 2012

S. Davoust ,
L. Jacquin  and
B. Leclaire
S. Davoust*
Affiliation:
ONERA, Department of Fundamental and Experimental Aerodynamics, 8 rue des Vertugadins, 92190 Meudon, France
L. Jacquin
Affiliation:
ONERA, Department of Fundamental and Experimental Aerodynamics, 8 rue des Vertugadins, 92190 Meudon, France
B. Leclaire
Affiliation:
ONERA, Department of Fundamental and Experimental Aerodynamics, 8 rue des Vertugadins, 92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

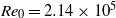The near field of a Reynolds number and low-Mach-number cylindrical jet has been investigated by means of a high-speed stereo PIV setup that provides the spatio-temporal velocity field in a transverse plane, two diameters downstream of the jet exit. Proper orthogonal decomposition (POD) and spatio-temporal correlations are used to identify some of the main dynamical features of this flow. We show that the flow is dominated by streamwise vortices whose production and spatial organization can be related to 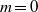and perturbations, and to the mean shear of the mixing layer. A dynamical scenario is proposed which describes this interaction, in accordance with our observations.

JFM classification

Wakes/Jets: Jets Wakes/Jets: Shear layers Turbulent Flows: Shear layer turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 709 , 25 October 2012 , pp. 408 - 444
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bernal, L. P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.CrossRefGoogle Scholar
2. Bradshaw, P. 1966 The effect of initial conditions on the development of a free shear layer. J. Fluid Mech. 26 (2), 225–236.Google Scholar
3. Brancher, P., Chomaz, J. M. & Huerre, P. 1994 Direct numerical simulations of round jets: vortex induction and side jets. Phys. Fluids 6 (5), 1768–1774.CrossRefGoogle Scholar
4. Bruun, H. H. 1995 Hot-Wire Anemometry: Principles and Signal Analysis. Oxford University Press.CrossRefGoogle Scholar
5. Champagnat, F., Plyer, A., Le Besnerais, G., Leclaire, B., Davoust, S. & Le Sant, Y. 2011 Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp. Fluids 50, 1169–1182.CrossRefGoogle Scholar
6. Citriniti, J. H. & George, W. K. 2000 Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 418, 137–166.CrossRefGoogle Scholar
7. Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48 (3), 547–591.CrossRefGoogle Scholar
8. Davoust, S. 2011 Dynamics of large-scale structures in turbulent jets with or without the effect of swirl. PhD thesis, ONERA, Ecole Polytechnique.Google Scholar
9. Davoust, S. & Jacquin, L. 2011 Taylor’s hypothesis convection velocities from mass conservation equation. Phys. Fluids 23 (5), 051701.CrossRefGoogle Scholar
10. Del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
11. Delville, J., Ukeiley, L., Cordier, L., Bonnet, J. P. & Glauser, M. 1999 Examination of large-scale structures in a turbulent plane mixing layer. Part 1. Proper orthogonal decomposition. J. Fluid Mech. 391, 91–122.CrossRefGoogle Scholar
12. Gamard, S., Jung, D. & George, W. K. 2004 Downstream evolution of the most energetic modes in a turbulent axisymmetric jet at high Reynolds number. Part 2. The far-field region. J. Fluid Mech. 514, 205–230.CrossRefGoogle Scholar
13. Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.CrossRefGoogle Scholar
14. George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. Adv. Turbul. 39–74.Google Scholar
15. Glauser, M. N. & George, W. K. 1987 Orthogonal decomposition of the axisymmetric jet mixing layer including azimuthal dependence. Adv. Turbul. 357–366.CrossRefGoogle Scholar
16. Ho, C. M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16, 365–422.Google Scholar
17. Hussain, A. K. M. F. & Zaman, K. B. M. Q. 1981 The preferred mode of the axisymmetric jet. J. Fluid Mech. 110, 39–71.CrossRefGoogle Scholar
18. Hussain, A. & Zedan, M. F. 1978 Effects of the initial condition on the axisymmetric free shear layer: effects of the initial momentum thickness. Phys. Fluids 21, 1100.CrossRefGoogle Scholar
19. Iqbal, M. O. & Thomas, F. O. 2007 Coherent structure in a turbulent jet via a vector implementation of the proper orthogonal decomposition. J. Fluid Mech. 571, 281–326.CrossRefGoogle Scholar
20. Jacquin, L., Leuchter, O., Cambon, C. & Mathieu, J. 1990 Homogeneous turbulence in the presence of rotation. J. Fluid Mech. 220, 1–52.Google Scholar
21. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
22. Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
23. Jung, D., Gamard, S. & George, W. K. 2004 Downstream evolution of the most energetic modes in a turbulent axisymmetric jet at high Reynolds number. Part 1. The near-field region. J. Fluid Mech. 514, 173–204.Google Scholar
24. Kim, J. 1983 On the structure of wall-bounded turbulent flows. Phys. Fluids 26, 2088.CrossRefGoogle Scholar
25. Kim, J. & Choi, H. 2009 Large eddy simulation of a circular jet: effect of inflow conditions on the near field. J. Fluid Mech. 620, 383–411.CrossRefGoogle Scholar
26. Leclaire, B. & Jacquin, L. 2012 On the generation of swirling jets: high Reynolds number rotating flow in a pipe with final contraction. J. Fluid Mech. 692, 78–111.CrossRefGoogle Scholar
27. Leclaire, B., Jaubert, B., Champagnat, F., Le Besnerais, G. & Le Sant, Y. 2009 FOLKI-3C: a simple, fast and direct algorithm for stereo PIV. In Proceedings of 8th International Symposium on Particle Image Velocimetry – PIV09. Melbourne.Google Scholar
28. Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.CrossRefGoogle Scholar
29. Lin, S. J. & Corcos, G. M. 1984 The mixing layer: deterministic models of a turbulent flow. Part 3. The effect of plane strain on the dynamics of streamwise vortices. J. Fluid Mech. 141, 139–178.CrossRefGoogle Scholar
30. Martin, J. E. & Meiburg, E. 1991 Numerical investigation of three-dimensionally evolving jets subject to axisymmetric and azimuthal perturbations. J. Fluid Mech. 230, 271–318.CrossRefGoogle Scholar
31. Matsuda, T. & Sakakibara, J. 2005 On the vortical structure in a round jet. Phys. Fluids 17, 025106.CrossRefGoogle Scholar
32. McIlwain, S. & Pollard, A. 2002 Large eddy simulation of the effects of mild swirl on the near field of a round free jet. Phys. Fluids 14, 653.CrossRefGoogle Scholar
33. Metcalfe, R. W., Orszag, S. A., Brachet, M. E., Menon, S. & Riley, J. J. 1987 Secondary instability of a temporally growing mixing layer. J. Fluid Mech. 184, 207–243.CrossRefGoogle Scholar
34. Michalke, A. 1984 Survey on jet instability theory. Prog. Aeronaut. Sci. 21 (3), 159–199.CrossRefGoogle Scholar
35. Neu, J. C. 1984 The dynamics of stretched vortices. J. Fluid Mech. 143, 253–276.CrossRefGoogle Scholar
36. Nickels, T. B. & Marusic, I. 2001 On the different contributions of coherent structures to the spectra of a turbulent round jet and a turbulent boundary layer. J. Fluid Mech. 448, 367–385.CrossRefGoogle Scholar
37. Paschereit, C. O., Oster, D., Long, T., Fiedler, H. E. & Wygnanski, I. 1992 Flow visualization of interactions among large coherent structures in an axisymmetric jet. Exp. Fluids 12 (3), 189–199.CrossRefGoogle Scholar
38. Raffel, M., Willert, C., Wereley, C. & Kompenhans, J. 2007 Particle Image Velocimetry. A Practical Guide, 2nd edn. Springer.CrossRefGoogle Scholar
39. Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.CrossRefGoogle Scholar
40. Suprayan, R. & Fiedler, H. E. 1994 On streamwise vortical structures in the near-field of axisymmetric shear layers. Meccanica 29 (4), 403–410.CrossRefGoogle Scholar
41. Thomas, F. O. 1991 Structure of mixing layers and jets. Appl. Mech. Rev. 44, 119.CrossRefGoogle Scholar
42. Tinney, C. E. 2009 Proper grid resolutions for the proper basis. AIAA 47th Aerospace Sciences Meeting and Exhibit, Orlando, Florida, USA, AIAA paper 2009–0068.Google Scholar
43. Tinney, C. E., Glauser, M. N. & Ukeiley, L. S. 2008a Low-dimensional characteristics of a transonic jet. Part 1. Proper orthogonal decomposition. J. Fluid Mech. 612, 107–141.CrossRefGoogle Scholar
44. Tinney, C. E., Glauser, M. N. & Ukeiley, L. S. 2008b Low-dimensional characteristics of a transonic jet. Part 2. Estimate and far-field prediction. J. Fluid Mech. 615, 53.CrossRefGoogle Scholar
45. Tropea, C., Yarin, A. L. & Foss, J. F. 2007 Springer Handbook of Experimental Fluid Mechanics. Springer.CrossRefGoogle Scholar
46. Yule, A. J. 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89 (3), 413–432.CrossRefGoogle Scholar
47. Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1981 Taylor hypothesis and large-scale coherent structures. J. Fluid Mech. 112, 379–396.CrossRefGoogle Scholar
48. Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1984 Natural large-scale structures in the axisymmetric mixing layer. J. Fluid Mech. 138, 325–351.CrossRefGoogle Scholar