Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-19T14:45:43.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of forced and unforced autophoretic particles

Published online by Cambridge University Press:  14 September 2022

R. Kailasham  and
Aditya S. Khair Open the ORCID record for Aditya S. Khair [Opens in a new window]
R. Kailasham
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Aditya S. Khair*
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

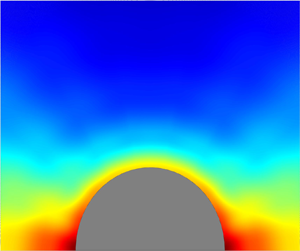
Chemically active, or autophoretic, particles that isotropically emit or absorb solute molecules undergo spontaneous self-propulsion when their activity is increased beyond a critical Péclet number ($Pe$). Here, we conduct numerical computations, using a spectral element based method, of a rigid, spherical autophoretic particle in unsteady rectilinear translation. The particle can be freely suspended (or ‘unforced’) or subject to an external force field (or ‘forced’). The motion of an unforced particle progresses through four regimes as $Pe$ is increased: quiescent, steady, stirring and chaos. The particle is stationary in the quiescent regime, and the solute profile is isotropic about the particle. At $Pe=4$ the fore–aft symmetry in the solute profile is broken, resulting in its steady self-propulsion. Our computations indicate that the self-propulsion speed scales linearly with $Pe-4$ near the onset of self-propulsion, as has been predicted in previous studies. A further increase in $Pe$ gives rise to the stirring regime at $Pe\approx 27$, where the fluid undergoes recirculation, while the particle remains essentially stationary. As $Pe$ is increased even further, the particle dynamics is marked by chaotic oscillations at $Pe\approx 55$ and higher, which we characterize in terms of the mean square displacement and velocity autocorrelation of the particle. Our results for an autophoretic particle under a weak external force are in good agreement with recent asymptotic predictions (Saha, Yariv & Schnitzer, J. Fluid Mech., vol. 916, 2021, p. A47). Additionally, we demonstrate that the strength and temporal scheduling of the external force may be tuned to modulate the chaotic dynamics at large $Pe$.

JFM classification

Complex Fluids: Active matter Complex Fluids: Colloids Nonlinear Dynamical Systems: Chaos
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 948 , 10 October 2022 , A41
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21 (1), 61–99.CrossRefGoogle Scholar
Bérge, P., Pomeau, Y. & Vidal, C. 1984 Order within Chaos: Towards a Deterministic Approach to Turbulence. John Wiley & Sons.Google Scholar
Campion–Renson, A. & Crochet, M.J. 1978 On the stream function–vorticity finite element solutions of Navier–Stokes equations. Intl J. Numer. Meth. Engng 12 (12), 1809–1818.CrossRefGoogle Scholar
Chen, Y., Chong, K.L., Liu, L., Verzicco, R. & Lohse, D. 2021 Instabilities driven by diffusiophoretic flow on catalytic surfaces. J. Fluid Mech. 919, A10.CrossRefGoogle Scholar
Chisholm, N.G., Legendre, D., Lauga, E. & Khair, A.S. 2016 A squirmer across Reynolds numbers. J. Fluid Mech. 796, 233–256.CrossRefGoogle Scholar
Donea, J. & Huerta, A. 2003 Finite Element Methods for Flow Problems. John Wiley & Sons.CrossRefGoogle Scholar
Farutin, A. & Misbah, C. 2021 Singular bifurcations: a regularization theory. arXiv2112.12094.Google Scholar
Hokmabad, B.V., Dey, R., Jalaal, M., Mohanty, D., Almukambetova, M., Baldwin, K.A., Lohse, D. & Maass, C.C. 2021 Emergence of bimodal motility in active droplets. Phys. Rev. X 11 (1), 011043.Google Scholar
Hu, W.F., Lin, T.S., Rafai, S. & Misbah, C. 2019 Chaotic swimming of phoretic particles. Phys. Rev. Lett. 123 (23), 238004.CrossRefGoogle ScholarPubMed
Hu, W.F., Lin, T.S., Rafai, S. & Misbah, C. 2022 Spontaneous locomotion of phoretic particles in three dimensions. Phys. Rev. Fluids 7 (3), 22–29.CrossRefGoogle Scholar
Izri, Z., Van Der Linden, M.N., Michelin, S. & Dauchot, O. 2014 Self-propulsion of pure water droplets by spontaneous marangoni-stress-driven motion. Phys. Rev. Lett. 113 (24), 248302.CrossRefGoogle ScholarPubMed
Khair, A.S. & Chisholm, N.G. 2014 Expansions at small Reynolds numbers for the locomotion of a spherical squirmer. Phys. Fluids 26 (1), 011902.CrossRefGoogle Scholar
Khair, A.S. & Chisholm, N.G. 2018 A higher-order slender-body theory for axisymmetric flow past a particle at moderate Reynolds number. J. Fluid Mech. 855, 421–444.CrossRefGoogle Scholar
Li, G. 2022 Swimming dynamics of a self-propelled droplet. J. Fluid Mech. 934, A20.CrossRefGoogle Scholar
Maass, C.C., Krüger, C., Herminghaus, S. & Bahr, C. 2016 Swimming droplets. Annu. Rev. Condens. Matter Phys. 7, 171–193.CrossRefGoogle Scholar
Michelin, S. 2023 Self-propulsion of chemically-active droplets. Annu. Rev. Fluid Mech. (in press).Google Scholar
Michelin, S. & Lauga, E. 2014 Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 747, 572–604.CrossRefGoogle Scholar
Michelin, S., Lauga, E. & Bartolo, D. 2013 Spontaneous autophoretic motion of isotropic particles. Phys. Fluids 25, 061701.CrossRefGoogle Scholar
Moerman, P. 2019 Dynamics of active droplets and freely jointed colloidal trimers. PhD thesis, Utrecht University.Google Scholar
Morozov, M. & Michelin, S. 2019 Nonlinear dynamics of a chemically-active drop: from steady to chaotic self-propulsion. J. Chem. Phys. 150 (4), 044110.CrossRefGoogle ScholarPubMed
Saha, S., Yariv, E. & Schnitzer, O. 2021 Isotropically active colloids under uniform force fields: from forced to spontaneous motion. J. Fluid Mech. 916, A47.CrossRefGoogle Scholar
Schnitzer, O. 2022 Weakly nonlinear dynamics of a chemically active particle near the threshold for spontaneous motion: adjoint method. Phys. Rev. Fluids. arXiv:2205.06136v4.Google Scholar
Strogatz, S. 2015 Nonlinear Dynamics and Chaos, 2nd edn. CRC Press.Google Scholar
Suda, S., Suda, T., Ohmura, T. & Ichikawa, M. 2021 Straight-to-curvilinear motion transition of a swimming droplet caused by the susceptibility to fluctuations. Phys. Rev. Lett. 127 (8), 088005.CrossRefGoogle ScholarPubMed
Tanaka, M., Matsumoto, T. & Yang, Q.F. 1994 Time-stepping boundary element method applied to 2-D transient heat conduction problems. Appl. Math. Model. 18 (10), 569–576.CrossRefGoogle Scholar
Yariv, E. 2020 Transient diffusion from high-capacity solute beacons. Appl. Maths Lett. 103, 106182.CrossRefGoogle Scholar