Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T01:30:49.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of drop impact on solid surfaces: evolution of impact force and self-similar spreading

Published online by Cambridge University Press:  08 February 2018

Leonardo Gordillo Open the ORCID record for Leonardo Gordillo [Opens in a new window] ,
Ting-Pi Sun  and
Xiang Cheng Open the ORCID record for Xiang Cheng [Opens in a new window]
Leonardo Gordillo*
Affiliation:
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA Departamento de Física, Universidad de Santiago, Casilla 307-2, Santiago, Chile
Ting-Pi Sun
Affiliation:
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA
Xiang Cheng*
Affiliation:
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the dynamics of drop impacts on dry solid surfaces. By synchronising high-speed photography with fast force sensing, we simultaneously measure the temporal evolution of the shape and impact force of impacting drops over a wide range of Reynolds numbers (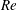$\mathit{Re}$). At high $\mathit{Re}$, when inertia dominates the impact processes, we show that the early time evolution of impact force follows a square-root scaling, quantitatively agreeing with a recent self-similar theory. This observation provides direct experimental evidence on the existence of upward propagating self-similar pressure fields during the initial impact of liquid drops at high 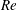$\mathit{Re}$. When viscous forces gradually set in with decreasing 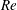$\mathit{Re}$, we analyse the early time scaling of the impact force of viscous drops using a perturbation method. The analysis quantitatively matches our experiments and successfully predicts the trends of the maximum impact force and the associated peak time with decreasing 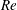$\mathit{Re}$. Furthermore, we discuss the influence of viscoelasticity on the temporal signature of impact forces. Last but not least, we also investigate the spreading of liquid drops at high 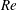$\mathit{Re}$ following the initial impact. Particularly, we find an exact parameter-free self-similar solution for the inertia-driven drop spreading, which quantitatively predicts the height of spreading drops at high 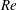$\mathit{Re}$. The limit of the self-similar approach for drop spreading is also discussed. As such, our study provides a quantitative understanding of the temporal evolution of impact forces across the inertial, viscous and viscoelastic regimes and sheds new light on the self-similar dynamics of drop-impact processes.

JFM classification

Boundary Layers: Boundary Layers Drops and Bubbles: Drops Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 190 - 214
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agbaglah, G., Josserand, C. & Zaleski, S. 2013 Longitudinal instability of a liquid rim. Phys. Fluids 25, 022103.CrossRefGoogle Scholar
Barenblatt, G. I. 1996 Scaling, Self-similarity, and Intermediate Asymptotics. Cambridge University Press.CrossRefGoogle Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Biancé, A.-L., Chevy, F., Clanet, C., Lagubeau, G. & Quéré, D. 2006 On the elasticity of an inertial liquid shock. J. Fluid Mech. 554, 47–66.CrossRefGoogle Scholar
Brodie, H. J. 1951 The splash-cup dispersal mechanism in plants. Can. J. Bot. 29, 224–234.Google Scholar
Clanet, C., Béguin, C., Richard, D. & Quéré, D. 2004 Maximal deformation of an impacting drop. J. Fluid Mech. 517, 199–208.Google Scholar
Deng, T., Varanasi, K. K., Hsu, M., Bhate, N., Keimel, C., Stein, J. & Blohm, M. 2009 Nonwetting of impinging droplets on textured surfaces. Appl. Phys. Lett. 94, 133109.Google Scholar
Dickerson, A. K., Shankles, P. G., Madhavan, N. M. & Hu, D. L. 2012 Mosquitoes survive raindrop collisions by virtue of their low mass. Proc. Natl Acad. Sci. USA 109, 9822–9827.Google Scholar
Driscoll, M. M. & Nagel, S. R. 2011 Ultrafast interference imaging of air in splashing dynamics. Phys. Rev. Lett. 107, 154502.Google Scholar
Eggers, J., Fontelos, M. A, Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22, 062101.CrossRefGoogle Scholar
Gamero-Castano, M., Torrents, A., Valdevit, L. & Zheng, J.-G. 2010 Pressure-induced amorphization in silicon caused by the impact of electrosprayed nanodroplets. Phys. Rev. Lett. 105, 145701.Google Scholar
Gart, S., Mates, J. E., Megaridis, C. M. & Jung, S. 2015 Droplet impacting a cantilever: a leaf-raindrop system. Phys. Rev. Appl. 3, 044019.Google Scholar
Grinspan, A. S. & Gnanamoorthy, R. 2010 Impact force of low velocity liquid droplets measured using piezoelectric PVDF film. Colloid. Surface A 356, 162–168.CrossRefGoogle Scholar
Hammitt, F. G. 1980 Cavitation and Multiphases Flow Phenomena. McGraw-Hill.Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.Google Scholar
Joung, Y. S. & Ruie, C. R. 2015 Aerosol generation by raindrop impact on soil. Nat. Commun. 6, 6083.Google Scholar
Klaseboer, E., Manica, R. & Chan, D. Y. C. 2014 Universal behavior of the initial stage of drop impact. Phys. Rev. Lett. 113, 194501.Google Scholar
Kolinski, J. M., Rubinstein, S. M., Mandre, S., Brenner, M. P., Weitz, D. A. & Mahadevan, L. 2012 Skating on a film of air: drops impacting on a surface. Phys. Rev. Lett. 108, 074503.Google Scholar
Krechetnikov, R. & Homsy, G. M. 2009 Crown-forming instability phenomena in the drop splash problem. J. Colloid Interface Sci. 331, 555–559.CrossRefGoogle ScholarPubMed
Kwon, H.-M., Paxson, A. T., Varanasi, K. K. & Patankar, N. A. 2011 Rapid deceleration-driven wetting transition during pendant drop deposition on superhydrophobic surfaces. Phys. Rev. Lett. 106, 036102.Google Scholar
Laan, N., de Bruin, K. G., Bartolo, D., Josserand, C. & Bonn, D. 2014 Maximum diameter of impacting liquid droplets. Phys. Rev. Appl. 2, 044018.Google Scholar
Lagubeau, G., Fontelos, M. A., Josserand, C., Maurel, A., Pagneux, V. & Petitjeans, P. 2012 Spreading dynamics of drop impacts. J. Fluid Mech. 713, 50–60.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1986 Theory of Elasticity, 3rd edn. Butterworth-Heinemann.Google Scholar
Li, J., Zhang, B., Guo, P. & Lv, Q. 2014 Impact force of a low speed water droplet colliding on a solid surface. J. Appl. Phys. 116, 214903.Google Scholar
Mani, M., Mandre, S. & Brenner, M. P. 2010 Events before droplet splashing on a solid surface. J. Fluid Mech. 647, 163–185.Google Scholar
Mongruel, A., Daru, V., Feuillebois, F. & Tabakova, S. 2009 Early post-impact time dynamics of viscous drops onto a solid dry surface. Phys. Fluids 21, 032101.Google Scholar
Nearing, M. A., Bradford, J. M. & Holtz, R. D. 1986 Measurement of force versus time relations for waterdrop impact. Soil Sci. Soc. Am. J. 50, 1532–1536.Google Scholar
Philippi, J., Lagrée, P.-Y. & Antkowiak, A. 2016 Drop impact on a solid surface: short-time self-similarity. J. Fluid Mech. 795, 96–135.Google Scholar
Rein, M. 1993 Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 12, 61–93.CrossRefGoogle Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
Rioboo, R., Marengo, M. & Tropea, C. 2002 Time evolution of liquid drop impact on solid dry surfaces. Exp. Fluids 33, 112–124.Google Scholar
Roisman, I. V. 2009 Inertia dominated drop collisions. II. An analytical solution of the Navier–Stokes equations for a spreading viscous film. Phys. Fluids 21, 052104.CrossRefGoogle Scholar
Roisman, I. V., Berberović, E. & Tropea, C. 2009 Inertia dominated drop collisions. I. On the universal flow in the lamella. Phys. Fluids 21, 052103.Google Scholar
Roisman, I. V., Rioboo, R. & Tropea, C. 2002 Normal impact of a liquid drop on a dry surface: model for spreading and receding. Proc. R. Soc. Lond. A 458, 1411–1430.Google Scholar
Savic, P. & Boult, G. T.1955 The fluid flow associated with the impact of liquid drops with solid surfaces. Rep. No. MT-26. Natl Res. Council Canada.Google Scholar
Soto, D., de Larivière, A. B., Boutillon, X., Clanet, C. & Quéré, D. 2014 The force of impacting rain. Soft Matt. 10, 4929–4934.Google Scholar
Tabakova, S., Feuillebois, F., Mongruel, A., Daru, V. & Radev, St. 2012 First stages of drop impact on a dry surface: asymptotic model. Z. Angew. Math. Phys. 63, 313–330.Google Scholar
Thanh-Vinh, N., Matsumoto, K. & Shimoyama, I. 2016 Pressure distribution on the contact area during the impact of a droplet on a textured surface. In 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), pp. 177–180. IEEE.Google Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. Parabolic Press.Google Scholar
Visser, C. W., Frommhold, P. E., Wildeman, S., Mettin, R., Lohse, D. & Sun, C. 2015 Dynamics of high-speed micro-drop impact: numerical simulations and experiments at frame-to-frame times below 100 ns. Soft Matt. 11, 1708–1722.Google Scholar
Wagner, H. 1932 Uber stoss- und gleitvorgange and der oberflache von flussigkeiten. Z. Angew. Math. Mech. 12, 193–215.Google Scholar
Wildeman, S., Visser, C. W., Sun, C. & Lohse, D. 2016 On the spreading of impacting drops. J. Fluid Mech. 805, 636–655.Google Scholar
Worthington, A. M. 1876a A second paper on the forms assumed by drops of liquids falling vertically on a horizontal plate. Proc. R. Soc. Lond. 25, 498–503.Google Scholar
Worthington, A. M. 1876b On the forms assumed by drops of liquids falling vertically on a horizontal plate. Proc. R. Soc. Lond. 25, 261–272.Google Scholar
Xu, L., Zhang, W. W. & Nagel, S. R. 2005 Drop splashing on a dry smooth surface. Phys. Rev. Lett. 94, 184505.Google Scholar
Yarin, A. L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 38, 159–192.Google Scholar
Zhang, B., Li, J., Guo, P. & Lv, Q. 2017 Experimental studies on the effect of Reynolds and Weber numbers on the impact forces of low-speed droplets colliding with a solid surface. Exp. Fluids 58, 125.Google Scholar
Zhao, R., Zhang, Q., Tjugito, H. & Cheng, X. 2015a Granular impact cratering by liquid drops: understanding raindrop imprints through an analogy to asteroid strikes. Proc. Natl Acad. Sci. USA 112, 342–347.Google Scholar
Zhao, S. C., de Jong, R. & van der Meer, D. 2015b Raindrop impact on sand: a dynamic explanation of crater morphologies. Soft Matt. 11, 6562–6568.Google Scholar

Gordillo et al. supplementary movie

Synchronized measurements on the kinematics and dynamics of impacting liquid drops. The first row shows the shape of impacting drops from high-speed photography. The second row shows the impact force of impacting drops as a function of time from force measurements. The third row shows the maximal height and the radius of spreading lamella measured based on the high-speed videos shown in the first row. High-speed photography and force measurements are synchronized. Liquid drops are made of silicone oils of various viscosities, which have diameter D = 2.2 ± 0.1 mm and impacting velocity U0 = 1.6 m/s. From left to right, different columns correspond to drops with kinematic viscosity ν = 50 cSt, 500 cSt, 5,000 cSt and 30,000 cSt, respectively.

Download Gordillo et al. supplementary movie(Video)
Video 2.3 MB