Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T09:02:10.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of buoyancy-driven flows at moderately high Atwood numbers

Published online by Cambridge University Press:  14 April 2016

Bhanesh Akula  and
Devesh Ranjan
Bhanesh Akula
Affiliation:
Department of Mechanical Engineering, Texas A&M University, 3123 TAMU, College Station, TX 77843-3123, USA
Devesh Ranjan*
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 801 Ferst Drive, Atlanta, GA 30332-0405, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

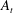Simultaneous density and velocity turbulence statistics for Rayleigh–Taylor-driven flows at a moderately high Atwood number ($A_{t}$) of 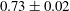$0.73\pm 0.02$ are obtained using a new convective type or statistically steady gas tunnel facility. Air and air–helium mixture are used as working fluids to create a density difference in this facility, with a thin splitter plate separating the two streams flowing parallel to each other at the same velocity (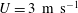$U=3~\text{m}~\text{s}^{-1}$). At the end of the splitter plate, the two miscible fluids are allowed to mix and the instability develops. Visualization and Mie-scattering techniques are used to obtain structure shape, volume fraction profile and mixing height growth information. Particle image velocimetry (PIV) and hot-wire techniques are used to measure planar and point-wise velocity statistics in the developing mixing layer. Asymmetry is evident in the flow field from the Mie-scattering images, with the spike side showing a more gradual decline in volume fraction than the bubble side. The spike side of the mixing layer grows 50 % faster than the bubble side. PIV is implemented for the first time in these moderately high-Atwood-number experiments (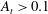$A_{t}>0.1$) to obtain root-mean-square velocities, anisotropy tensor components and Reynolds stresses across the mixing layer. Overall, the turbulence statistics measured have shown different scaling compared to small-Atwood-number experiments. However, the total probability density functions for the velocities and turbulent mass fluxes exhibit behaviour similar to small-Atwood-number experiments. Conditional statistics reveal different values for turbulence statistics for spikes and bubbles, unlike small-Atwood-number experiments.

JFM classification

Convection: Buoyancy-driven instability Instability: Nonlinear instability Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 313 - 355
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akula, B.2014 Experimental investigation of buoyancy driven mixing with and without shear at different Atwood numbers. PhD thesis, Texas A&M University.Google Scholar
Akula, B., Andrews, M. J. & Ranjan, D. 2013 Effect of shear on Rayleigh–Taylor mixing at small Atwood number. Phys. Rev. E 87, 033013.Google Scholar
Andrews, M. J. & Dalziel, S. B. 2010 Small Atwood number Rayleigh–Taylor experiments. Phil. Trans. R. Soc. A 368, 1663–1679.CrossRefGoogle ScholarPubMed
Andrews, M. J. & Spalding, D. B. 1990 A simple experiment to investigate two-dimensional mixing by Rayleigh–Taylor instability. Phys. Fluids A 2, 922–927.CrossRefGoogle Scholar
Arons, J. & Lea, S. M. 1976 Accretion onto magnetized neutron stars – structure and interchange instability of a model magnetosphere. Astrophys. J. 207, 914–936.Google Scholar
Banerjee, A. & Andrews, M. J. 2006 Statistically steady measurements of Rayleigh–Taylor mixing in a gas channel. Phys. Fluids 18, 035107.Google Scholar
Banerjee, A. & Andrews, M. J. 2009 3D simulations to investigate initial condition effects on the growth of Rayleigh–Taylor mixing. Int. J. Heat Mass Transfer 52, 3906–3917.Google Scholar
Banerjee, A., Kraft, W. N. & Andrews, M. J. 2010 Detailed measurements of a statistically steady Rayleigh–Taylor mixing layer from small to high Atwood numbers. J. Fluid Mech. 659, 127–190.Google Scholar
Bell, J. H. & Mehta, R. D.1989 Design and calibration of the mixing layer and wind tunnel NASA Rep. JIAA TR-89.Google Scholar
Bell, J. H. & Mehta, R. D. 1990 Development of two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28, 2034–2042.Google Scholar
Birkhoff, G. & Carter, D. 1957 Rising plane bubbles. J. Rat. Mech. Anal. 6, 769–779.Google Scholar
Bruun, H. H. 1995 Hot-Wire Anemometry: Principles and Signal Analysis. Oxford University Press.Google Scholar
Budil, K. S., Remington, B. A., Weber, S. V., Perry, T. S. & Peyser, T. A.1997 Nonlinear Rayleigh–Taylor instability experiments in nova. Lawrence Livermore National Lab. Report, UCRL-JC-127732.Google Scholar
Burrows, A. 2000 Supernova explosions in the universe. Nature 403, 727–733.Google Scholar
Burton, G. C. 2011 Study of ultrahigh Atwood-number Rayleigh–Taylor mixing dynamics using the nonlinear large-eddy simulation method. Phys. Fluids 23 (4), 045106.Google Scholar
Cabot, W. H. & Cook, A. W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type Ia supernovae. Nat. Phys. 2, 562–568.Google Scholar
Carter, B. A., Retterer, J. M., Yizengaw, E., Wiens, K., Wing, S., Groves, K., Caton, R., Bridgwood, C., Francis, M., Terkildsen, M. et al. 2014 Using solar wind data to predict daily GPS scintillation occurrence in the African and Asian low-latitude regions. Geophys. Res. Lett. 41, 8176–8184.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Cole, R. L. & Tankin, R. S. 1973 Experimental study of Taylor instability. Phys. Fluids 16, 1810–1815.Google Scholar
Cook, A. W. & Dimotakis, P. E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.Google Scholar
Daly, B. J. 1967 Numerical study of two fluid Rayleigh–Taylor instability. Phys. Fluids 10, 297–307.CrossRefGoogle Scholar
Dalziel, S. B. 1993 Rayleigh–Taylor instability: experiments with image analysis. Dyn. Atmos. Oceans 20, 127–153.Google Scholar
Dalziel, S. B., Linden, P. F. & Youngs, D. L. 1999 Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.Google Scholar
Danckwerts, P. V. 1952 The definition and measurement of some characteristics of mixtures. Appl. Sci. Res. 3, 279–296.Google Scholar
Davies, R. M. & Taylor, G. 1950 The mechanics of large bubbles rising through extended liquids and through liquids in tubes. Proc. R. Soc. Lond. A 200, 375–390.Google Scholar
Dimonte, G., Ramaprabhu, P. K., Youngs, D. L., Andrews, M. J. & Rosner, R. 2005 Recent advances in the turbulent Rayleigh–Taylor instability. Phys. Plasmas 12, 056301.CrossRefGoogle Scholar
Dimonte, G. & Schneider, M. 1996 Turbulent Rayleigh–Taylor instability experiments with variable acceleration. Phys. Rev. E 54, 3740.Google Scholar
Dimonte, G. & Schneider, M. 2000 Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12, 304–321.CrossRefGoogle Scholar
Dimonte, G., Youngs, D. L., Dimits, A., Weber, S., Marinak, M., Wunsch, S., Garasi, C., Robinson, A., Andrews, M. J. & Ramaprabhu, P. K. 2004 A comparative study of the turbulent Rayleigh–Taylor instability using high-resolution three-dimensional numerical simulations: the Alpha-Group Collaboration. Phys. Fluids 16, 1668.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Emmons, H. W., Chang, C. T. & Watson, B. C. 1960 Taylor instability of finite surface waves. J. Fluid Mech. 7, 177–193.Google Scholar
Fermi, E. & Neumann, J. V.1955 Taylor instability of incompressible liquids. United States Atomic Energy Commission: Unclassified, AECU-2979.Google Scholar
Girimaji, S. S. 2000 Pressure–strain correlation modelling of complex turbulent flows. J. Fluid Mech. 422, 91–123.Google Scholar
Goncharov, V. N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88, 134502.Google Scholar
Groth, J. & Johansson, A. V. 1988 Turbulence reduction by screens. J. Fluid Mech. 197, 139–155.Google Scholar
Haan, S. W. 1989 Onset of nonlinear saturation for Rayleigh–Taylor growth in the presence of a full spectrum of modes. Phys. Rev. A 39, 5812.Google Scholar
Hachisu, I., Matsuda, T., Nomoto, K. & Shigeyama, T. 1991 Rayleigh–Taylor instabilities and mixing in the helium star models for type Ib/Ic supernovae. Astrophys. J. 368, L27–L30.Google Scholar
Huang, Z., De Luca, A., Atherton, T. J., Bird, M., Rosenblatt, C. & Carls, P. 2007 Rayleigh–Taylor instability experiments with precise and arbitrary control of the initial interface shape. Phys. Rev. Lett. 99, 204502.CrossRefGoogle ScholarPubMed
Koop, C. G. 1976 Instability and turbulence in a stratified shear layer. NASA STI/Recon Tech. Rep. N 77, 16303.Google Scholar
Kraft, W. N.2008 Simultaneous and instantaneous measurement of velocity and density in Rayleigh–Taylor mixing layers. PhD thesis, Texas A&M University.Google Scholar
Kraft, W. N., Banerjee, A. & Andrews, M. J. 2009 On hot-wire diagnostics in Rayleigh–Taylor mixing layers. Exp. Fluids 47, 49–68.CrossRefGoogle Scholar
Kucherenko, Y. A., Balabin, S. I., Ardashova, R. I., Kozelkov, O. E., Dulov, A. V. & Romanov, I. A. 2003 Experimental study of the influence of the stabilizing properties of transitional layers on the turbulent mixing evolution. Laser Part. Beams 21, 369–373.Google Scholar
Kuchibhatla, S. & Ranjan, D. 2012 Rayleigh–Taylor experiments. In ASME 2012 International Mechanical Engineering Congress and Exposition, pp. 1341–1351. American Society of Mechanical Engineers.Google Scholar
Kuchibhatla, S. & Ranjan, D. 2013 Effect of initial conditions on Rayleigh–Taylor mixing: modal interaction. Phys. Scr. 155, 014057.Google Scholar
Laws, E. M. & Livesey, J. L. 1978 Flow through screens. Annu. Rev. Fluid Mech. 10, 247–266.Google Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. J. 122 (1), 1–12.CrossRefGoogle Scholar
Lewis, D. J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II. Proc. R. Soc. Lond. A 202, 81–96.Google Scholar
Livescu, D., Ristorcelli, J. R., Gore, R. A., Dean, S. H., Cabot, W. H. & Cook, A. W. 2009 High-Reynolds number Rayleigh–Taylor turbulence. J. Turbul. 10 (13), 1–32.Google Scholar
Livescu, D., Wei, T. & Petersen, M. R. 2011 Direct numerical simulations of Rayleigh–Taylor instability. J. Phys.: Conf. Ser. 318, 082007.Google Scholar
Loehrke, R. I. & Nagib, H. M.1972 Experiments on management of free-stream turbulence. AGARD Report No. 598.Google Scholar
Loehrke, R. I. & Nagib, H. M. 1976 Control of free-stream turbulence by means of honeycombs: a balance between suppression and generation. J. Fluids Engng 98, 342–351.Google Scholar
McFarland, J. A., Greenough, J. A. & Ranjan, D. 2011 Computational parametric study of a Richtmyer–Meshkov instability for an inclined interface. Phys. Rev. E 84, 026303.CrossRefGoogle ScholarPubMed
McFarland, J. A., Reilly, D., Creel, S., McDonald, C., Finn, T. & Ranjan, D. 2014 Experimental investigation of the inclined interface Richtmyer–Meshkov instability before and after reshock. Exp. Fluids 55 (1), 1–14.Google Scholar
Mueschke, N. J.2008 Experimental and numerical study of molecular mixing dynamics in Rayleigh–Taylor unstable flows. PhD thesis, Texas A&M University.Google Scholar
Mueschke, N. J., Andrews, M. J. & Schilling, O. 2006 Experimental characterization of initial conditions and spatio-temporal evolution of a small-Atwood-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 567, 27–63.Google Scholar
Mueschke, N. J. & Schilling, O. 2009a Investigation of Rayleigh–Taylor turbulence and mixing using direct numerical simulation with experimentally measured initial conditions. I. Comparison to experimental data. Phys. Fluids 21, 014106.Google Scholar
Mueschke, N. J. & Schilling, O. 2009b Investigation of Rayleigh–Taylor turbulence and mixing using direct numerical simulation with experimentally measured initial conditions. II. Dynamics of transitional flow and mixing statistics. Phys. Fluids 21, 014107.Google Scholar
Mueschke, N. J., Schilling, O., Youngs, D. L. & Andrews, M. J. 2009 Measurements of molecular mixing in a high-Schmidt-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 632, 17–48.Google Scholar
Olson, D. H. & Jacobs, J. W. 2009 Experimental study of Rayleigh–Taylor instability with a complex initial perturbation. Phys. Fluids 21, 034103.Google Scholar
Papoulis, A. & Pillai, S. U. 2002 Probability, Random Variables and Stochastic Processes, 4th edn. McGraw-Hill.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Ramaprabhu, P., Dimonte, G., Woodward, P., Fryer, C., Rockefeller, G., Muthuraman, K., Lin, P.-h. & Jayaraj, J. 2012 The late-time dynamics of the single-mode Rayleigh–Taylor instability. Phys. Fluids 24 (7), 074107.Google Scholar
Ramaprabhu, P. K.2003 On the dynamics of Rayleigh–Taylor mixing. PhD thesis, Texas A&M University.Google Scholar
Ramaprabhu, P. K. & Andrews, M. J. 2003 Simultaneous measurements of velocity and density in buoyancy-driven mixing. Exp. Fluids 34, 98–106.Google Scholar
Ramaprabhu, P. K. & Andrews, M. J. 2004a Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.CrossRefGoogle Scholar
Ramaprabhu, P. K. & Andrews, M. J. 2004b On the initialization of Rayleigh–Taylor simulations. Phys. Fluids 16 (8), L59–L62.CrossRefGoogle Scholar
Ramaprabhu, P. K., Dimonte, G. & Andrews, M. J. 2005 A numerical study of the influence of initial perturbations on the turbulent Rayleigh–Taylor instability. J. Fluid Mech. 536, 285–319.Google Scholar
Ratafia, M. 1973 Experimental investigation of Rayleigh–Taylor instability. Phys. Fluids 16, 1207–1210.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Lond. Math. Soc. 14, 170–177.Google Scholar
Read, K. I. 1984 Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 45–58.CrossRefGoogle Scholar
Remington, B. A., Weber, S. V., Marinak, M. M., Haan, S. W., Kilkenny, J. D., Wallace, R. & Dimonte, G. 1994 Multimode Rayleigh–Taylor experiments on nova. Phys. Rev. Lett. 73, 545–548.Google Scholar
Ristorcelli, J. R. & Clark, T. T. 2004 Rayleigh–Taylor turbulence: self-similar analysis and direct numerical simulations. J. Fluid Mech. 507, 213–253.Google Scholar
Sazonov, S. V. 1991 Dissipative structures in the f-region of the equatorial ionosphere generated by Rayleigh–Taylor instability. Planet. Space Sci. 39, 1667–1671.CrossRefGoogle Scholar
Schubauer, G. B., Spangenberg, W. G. & Klebanoff, P. S.1950 Aeodynamic characteristics of damping screens. NACA TN 2001.Google Scholar
Sharp, D. H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12, 3–18.CrossRefGoogle Scholar
Snider, D. M.1994 A study of compound buoyancy and shear mixing. PhD thesis, Texas A&M University.Google Scholar
Snider, D. M. & Andrews, M. J. 1994 Rayleigh–Taylor and shear driven mixing with an unstable thermal stratification. Phys. Fluids 6, 3324.Google Scholar
Tan-Atichat, J., Nagib, H. M. & Loehrke, R. I. 1982 Interaction of free-stream turbulence with screens and grids: a balance between turbulence scales. J. Fluid Mech. 114, 501–528.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Tsiklashvili, V., Colio, PE. R., Likhachev, O. A. & Jacobs, J. W. 2012 An experimental study of small Atwood number Rayleigh–Taylor instability using the magnetic levitation of paramagnetic fluids. Phys. Fluids 24, 052106.Google Scholar
Waddell, J. T., Niederhaus, C. E. & Jacobs, J. W. 2001 Experimental study of Rayleigh–Taylor instability: low Atwood number liquid systems with single-mode initial perturbations. Phys. Fluids 13, 1263–1273.Google Scholar
White, J., Oakley, J., Anderson, M. & Bonazza, R. 2010 Experimental measurements of the nonlinear Rayleigh–Taylor instability using a magnetorheological fluid. Phys. Rev. E 81, 026303.Google Scholar
Wilcock, W. S. D. & Whitehead, J. A. 1991 The Rayleigh–Taylor instability of an embedded layer of low-viscosity fluid. J. Geophys. Res. 96, 12193–12200.Google Scholar
Wilke, C. R. 1950 A viscosity equation for gas mixtures. J. Chem. Phys. 18, 517–519.Google Scholar
Wilson, P. N.2002 A study of buoyancy and shear driven turbulence within a closed water channel. PhD thesis, Texas A&M University.Google Scholar
Wilson, P. N. & Andrews, M. J. 2002 Spectral measurements of Rayleigh–Taylor mixing at small Atwood number. Phys. Fluids 14, 938–945.CrossRefGoogle Scholar
Wilson, P. N., Andrews, M. J. & Harlow, F. 1999 Spectral nonequilibrium in a turbulent mixing layer. Phys. Fluids 11, 2425–2433.Google Scholar
Youngs, D. L. 1984 Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 32–44.Google Scholar
Youngs, D. L. 1991 Three dimensional numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Phys. Fluids A 3, 1312.Google Scholar