Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T15:43:44.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamic simulation of a coated microbubble in an unbounded flow: response to a step change in pressure

Published online by Cambridge University Press:  07 June 2017

M. Vlachomitrou  and
N. Pelekasis Open the ORCID record for N. Pelekasis [Opens in a new window]
M. Vlachomitrou
Affiliation:
Department of Mechanical Engineering, University of Thessaly, Leoforos Athinon, Pedion Areos, 38834 Volos, Greece
N. Pelekasis*
Affiliation:
Department of Mechanical Engineering, University of Thessaly, Leoforos Athinon, Pedion Areos, 38834 Volos, Greece
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A numerical method is developed to study the dynamic behaviour of an encapsulated bubble when the viscous forces of the surrounding liquid are accounted for. The continuity and Navier–Stokes equations are solved for the liquid, whereas the coating is described as a viscoelastic shell with bending resistance. The Galerkin Finite Element Methodology is employed for the spatial discretization of the flow domain surrounding the bubble, with the standard staggered grid arrangement that uses biquadratic and bilinear Lagrangian basis functions for the velocity and pressure in the liquid, respectively, coupled with a superparametric scheme with 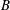$B$-cubic splines as basis functions pertaining to the location of the interface. The spine method and the elliptic mesh generation technique are used for updating the mesh points in the interior of the flow domain as the shape of the interface evolves with time, with the latter being distinctly superior in capturing severely distorted shapes. The stabilizing effect of the liquid viscosity is demonstrated, as it alters the amplitude of the disturbance for which a bubble deforms and/or collapses. For a step change in the far-field pressure the dynamic evolution of the microbubble is captured until a static equilibrium is achieved. Static shapes that are significantly compressed are captured in the post-buckling regime, leading to symmetric or asymmetric shapes, depending on the relative dilatation to bending stiffness ratio. As the external overpressure increases, shapes corresponding to all the solution families that were captured evolve to exhibit contact as the two poles approach each other. Shell viscosity prevents jet formation by relaxing compressive stresses and bending moments around the indentation generated at the poles due to shell buckling. This behaviour is conjectured to be the inception process leading to static shapes with contact regions.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Drops and Bubbles: Bubble dynamics Biological Fluid Dynamics: Capsule/cell dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 717 - 761
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babuska, I. 1973 The finite element method with Lagrangian multipliers. Numer. Math. 20, 179–192.Google Scholar
Barthes-Biesel, D., Diaz, A. & Dhenin, E. 2002 Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation. J. Fluid Mech 460, 211–222.Google Scholar
Barthes-Biesel, D. & Sgaier, H. 1985 Role of membrane viscosity in the orientation and deformation of a spherical capsule in shear flow. J. Fluid Mech. 160, 119–135.Google Scholar
Blake, J. R., Hooton, M. C., Robinson, P. B. & Tong, R. P. 1997 Collapsing cavities, toroidal bubbles and jet impact. Phil. Trans. R. Soc. Lond. A 355, 537–550.Google Scholar
Blake, J. R., Keen, G. S., Tong, R. P. & Wilson, M. 1999 Acoustic cavitation: the fluid dynamics of non-spherical bubbles. Phil. Trans. R. Soc. Lond. A 357, 251–267.Google Scholar
Chatzidai, N., Giannousakis, A., Dimakopoulos, Y. & Tsamopoulos, J. 2009 On the elliptic mesh generation in domains containing multiple inclusions and undergoing large deformations. J. Comput. Fluids 228, 1980–2011.Google Scholar
Chen, H., Kreider, W., Brayman, A. A., Bailey, M. R. & Matula, T. J. 2011 Blood vessel deformations on microsecond time scales by ultrasonic cavitation. Phys. Rev. Lett. 106 (3), 034301.Google Scholar
Chen, T.-Y. & Tsamopoulos, J. 1993 Nonlinear dynamics of capillary bridges: theory. J. Fluid Mech. 255, 373–409.Google Scholar
Christodoulou, K. N. & Scriven, L. E. 1992 Discretization of free surface flows and other moving boundary problems. J. Comput. Phys. 99, 39–55.Google Scholar
Church, C. C. 1995 The effects of an elastic solid surface layer on the radial pulsations of gas bubbles. J. Acoust. Soc. Am. 97, 1510–1521.Google Scholar
Dear, J. P. & Field, J. E. 1988 A study of the collapse of an array of cavities. J. Fluid Mech. 19, 409–425.Google Scholar
De Jong, N., Emmer, M., Chin, C. T., Bouakaz, A., Mastik, F., Lohse, D. & Versluis, M. 2007 ‘Compression-only’ behavior of phospholipid-coated contrast bubbles. Ultrasound Med. Biol. 33 (4), 653–656.Google Scholar
Dimakopoulos, Y. & Tsamopoulos, J. 2003 A quasi-elliptic transformation for moving boundary problems with large anisotropic deformations. J. Comput. Phys. 192, 494–522.Google Scholar
Doinikov, A. 2004 Translational motion of a bubble undergoing shape oscillations. J. Fluid Mech. 501, 1–24.Google Scholar
Dollet, B., Van der Meer, S. M., Garbin, V., de Jong, N., Lohse, D. & Versluis, M. 2008 Nonspherical oscillations of ultrasound contrast agent microbubbles. Ultrasound Med. Biol. 34, 1465–1473.Google Scholar
Elman, H., Silvester, D. & Wathen, A. 2005 Finite Elements and Fast Iterative Solvers. Oxford Science Publications.Google Scholar
Ferrara, K., Pollard, R. & Borden, M. 2007 Ultrasound microbubble contrast agents: fundamentals and application to gene and drug delivery. Annu. Rev. Biomed. Engng 9 (1), 415–447.Google Scholar
Foteinopoulou, K., Mavratzas, V. & Tsamopoulos, J. 2004 Numerical simulation of bubble growth in Newtonian viscoelastic filaments undergoing stretching. J. Non-Newtonian Fluid Mech. 122, 177–200.CrossRefGoogle Scholar
Katiyar, A. & Sarkar, K. 2011 Excitation threshold for subharmonic generation from contrast microbubbles. J. Acoust. Soc. Am. 130 (5), 3137–3147.Google Scholar
Kaufmann, B. A., Wei, K. & Linder, J. R. 2007 Contrast echocardiography. Curr. Probl. Cardiol. 32 (2), 51–96.Google Scholar
Khismatullin, D. B. & Nadim, A. 2002 Radial oscillations of encapsulated microbubbles. Phys. Fluids 14, 3534–3556.Google Scholar
Kistler, S. F. & Scriven, L. E. 1983 Coating Flows in Computational Analysis of Polymer Processing (ed. Pearson, J. R. A. & Richardson, S. M.), chap. 8, pp. 24–299. Applied Science Publishers.Google Scholar
Knoche, S. & Kierfeld, J. 2011 Buckling of spherical capsules. Phys. Rev. E 84 (4), 046608.Google Scholar
Lauterborn, W. & Bolle, H. 1975 Experimental investigations of cavitation-bubble collapse in the neighborhood of a solid boundary. J. Fluid Mech. 72 (02), 391–399.Google Scholar
Liu, Y., Sugiyama, K., Takagi, S. & Matsumoto, Y. 2011 Numerical study on the shape oscillation of an encapsulated microbubble in ultrasound field. Phys. Fluids 23, 041904.Google Scholar
Lytra, A. & Pelekasis, N. 2014 Static response and stability of coated microbubbles – multiplicity of solutions and parameter estimation. Fluid Dyn. Res. 46, 041422.Google Scholar
Marmottant, P., Bouakaz, A., de Jong, N. & Quilliet, C. 2011 Buckling resistance of solid shell bubbles under ultrasound. J. Acoust. Soc. Am. 129 (3), 1231–1239.Google Scholar
Marmottant, P., van der Meer, S., Emmer, M., Versluis, M., de Jong, N., Hilgenfeldt, S. & Lohse, D. 2005 A model for large amplitude oscillations of coated bubbles accounting for buckling and rupture. J. Acoust. Soc. Am. 118 (6), 3499.CrossRefGoogle Scholar
Notz, P. K. & Basaran, O. A. 1999 Dynamics of drop formation in an electric field. J. Colloid Interface Sci. 213 (1), 218–237.Google Scholar
Notz, P. K. & Basaran, O. A. 2004 Dynamics and breakup of contracting liquid filament. J. Fluid Mech. 512, 223–256.Google Scholar
Overvelde, M.2010 Ultrasound contrast agents: dynamics of coated bubbles. PhD thesis, University of Twente, Netherlands.Google Scholar
Patzek, T. W., Basaran, O. A., Benner, R. E. & Scriven, L. E. 1995 Nonlinear oscillations of two-dimensional, rotating inviscid drops. J. Comput. Phys. 116, 3–25.Google Scholar
Pelekasis, N. A. & Tsamopoulos, J. A. 1993a Bjerknes forces between two bubbles. Part 1. Response to a step change in pressure. J. Fluid Mech. 254, 467–499.Google Scholar
Pelekasis, N. A. & Tsamopoulos, J. A. 1993b Bjerknes forces between two bubbles. Part 2. Response to an oscillatory pressure field. J. Fluid Mech. 254, 501–527.Google Scholar
Pelekasis, N. A., Tsamopoulos, J. A. & Manolis, G. D. 1992 A hybrid finite-boundary element method for inviscid flows with free surface. J. Comput. Phys. 101, 231–251.Google Scholar
Pozrikidis, C. 2001 Effect of membrane bending stiffness on the deformation of capsules in simple shear flow. J. Fluid Mech. 440, 269–291.Google Scholar
Qin, S. & Ferrara, K. W. 2006 Acoustic response of compliable microvessels containing ultrasound contrast agents. Phys. Med. Biol. 51, 5065–5088.Google Scholar
Ryskin, G. & Leal, L. G. 1983 Orthogonal mapping. J. Comput. Phys. 50, 71–100.Google Scholar
Shi, W. T. & Forsberg, F. 2000 Ultrasonic characterization of the nonlinear properties of contrast microbubbles. Ultrasound Med. Biol. 26 (1), 93–104.Google Scholar
Popinet, S. & Zaleski, S. 2002 Bubble collapse near a solid boundary: a numerical study of the influence of viscosity. J. Fluid Mech. 464, 137–163.Google Scholar
Saad, Y. 1996 Iterative Methods for Sparse Linear Systems. PWS.Google Scholar
Saad, Y. & Schultz, M. H. 1986 GMRES: a generalized minimal residual algorithm for solving non-symmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869.Google Scholar
Saito, H. & Scriven, L. E. 1981 Study of coating flow by the finite element method. J. Comput. Phys. 42, 53–76.Google Scholar
Sarkar, K., Shi, W. T., Chatterjee, D. & Forsberg, F. 2005 Characterization of ultrasound contrast microbubbles using in vitro experiments and viscous and viscoelastic interface models for encapsulation. J. Acoust. Soc. Am. 118 (1), 539–550.Google Scholar
Takagi, S., Matsumoto, Y. & Huang, H. 1997 Numerical analysis of a single rising bubble using boundary-fitted coordinate system. JSME Intl J. B40, 42–50.Google Scholar
Thomas, D. H., Looney, P., Steel, R., Pelekasis, N., Mcdicken, W. N., Anderson, T. & Sboros, V. 2009 Acoustic detection of microbubble resonance. Appl. Phys. Lett. 94 (24), 243902.CrossRefGoogle Scholar
Timoshenko, P. & Woinowsky-Krieger, S. 1959 Theory of Plates and Shells. McGraw-Hill.Google Scholar
Tsiglifis, K. & Pelekasis, N. 2007 Nonlinear oscillations and collapse of elongated bubbles subject to weak viscous effects: effect of internal overpressure. Phys. Fluids 19, 072106.Google Scholar
Tsiglifis, K. & Pelekasis, N. 2008 Nonlinear radial oscillations of encapsulated microbubbles subject to ultrasound: the effect of membrane constitutive law. J. Acoust. Soc. Am. 123 (6), 4059–4070.Google Scholar
Tsiglifis, K. & Pelekasis, N. 2011 Parametric stability and dynamic buckling of encapsulated microbubble subject to acoustic disturbances. Phys. Fluids 23, 012102.Google Scholar
Tsiglifis, K. & Pelekasis, N. 2013 Simulations of insonated contrast agents: saturation and transient break-up. Phys. Fluids 25, 032109.Google Scholar
Tsiveriotis, K. & Brown, R. A. 1992 Boundary-conforming mapping applied to computations of highly deformed solidification interfaces. Intl J. Numer. Meth. Fluids 14, 981–1003.Google Scholar
Van der Meer, M., Dollet, B., Voormolen, M. M., Chin, C. T., Bouakaz, A., de Jong, N., Versluis, M. & Lohse, D. 2007 Microbubble spectroscopy of ultrasound contrast agents. J. Am. Stat. Assoc. 121, 648.Google Scholar
Vos, H. J., Dollet, B., Bosch, J. G., Versluis, M. & de Jong, N. 2008 Nonspherical vibrations of microbubbles in contact with a wall: a pilot study at low mechanical index. Ultrasound Med. Biol. 34 (4), 685–688.Google Scholar
Widjaja, E., Liu, N-C., Li, M., Collins, R. T., Basaran, O. A. & Harris, M. T. 2007 Dynamics of sessible droplet evaporation: a comparison of the spine and the elliptic mesh generation methods. Comput. Chem. Engng 31, 219–232.Google Scholar
Zarda, P. R., Chien, S. & Skalak, R. 1977 Elastic deformations of red blood cells. J. Biomech. 10, 211–221.Google Scholar
Zhao, S., Ferrara, K. W. & Dayton, P. A. 2005 Asymmetric oscillation of adherent targeted ultrasound contrast agents. Appl. Phys. Lett. 87, 134103.Google Scholar