Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T15:58:27.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamic and stationary shapes of rotating toroidal drops in viscous linear flows

Published online by Cambridge University Press:  21 July 2021

Sumit Malik Open the ORCID record for Sumit Malik [Opens in a new window] ,
O.M. Lavrenteva Open the ORCID record for O.M. Lavrenteva [Opens in a new window]  and
A. Nir Open the ORCID record for A. Nir [Opens in a new window]
Sumit Malik
Affiliation:
Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa3200003, Israel
O.M. Lavrenteva
Affiliation:
Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa3200003, Israel
A. Nir*
Affiliation:
Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa3200003, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

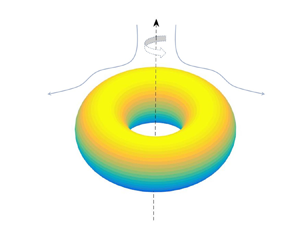
Dynamic and stationary axisymmetric deformation of viscous toroidal drops submerged in slow viscous flow are studied numerically. The immiscible ambient fluid is subject to a combination of rotation and extensional/compressional (biextensional) flow. The creeping flow approximation is assumed. The numerical simulations are performed with the help of the boundary integral method. The process under consideration is governed by three dimensionless parameters: the capillary number that characterizes the ratio of viscous and surface tension forces; the Bond number, that characterizes the ratio of centrifugal and surface tension forces; and the ratio of viscosity of the two fluids. Our simulations for the equal viscosity case demonstrated that, depending on the governing parameters, the toroidal drop either collapses, extends indefinitely or it attains a stationary toroidal shape. The latter may be stable or unstable with respect to axisymmetric disturbances. Conditions for the realization of each of the dynamic regimes and stationary states in terms of governing parameters are presented. In particular, stable toroidal shapes result under the combined action of rotation and extensional flow, and were not found under the action of rotation and compressional flow.

JFM classification

Drops and Bubbles: Drops Mathematical Foundations: Computational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , A3
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

An, D., Warning, A., Yancey, K.G., Chang, C.-T., Kern, V.R., Datta, A.K., Steen, P.H., Luo, D. & Ma, M. 2016 Mass production of shaped particles through vortex ring freezing. Nat. Commun. 7 (1), 1–10.CrossRefGoogle ScholarPubMed
Aussillous, P. & Quéré, D. 2004 Shapes of rolling liquid drops. J. Fluid Mech. 512, 133.CrossRefGoogle Scholar
Baumann, N., Joseph, D.D., Mohr, P. & Renardy, Y. 1992 Vortex rings of one fluid in another in free fall. Phys. Fluids A 4 (3), 567–580.CrossRefGoogle Scholar
Champion, J.A., Katare, Y.K. & Mitragotri, S. 2007 Particle shape: a new design parameter for micro-and nanoscale drug delivery carriers. J. Control Release 121 (1–2), 3–9.CrossRefGoogle ScholarPubMed
Chang, Y.-W., Fragkopoulos, A.A., Marquez, S.M., Kim, H.D., Angelini, T.E. & Fernández-Nieves, A. 2015 Biofilm formation in geometries with different surface curvature and oxygen availability. New J. Phys. 17 (3), 033017.CrossRefGoogle Scholar
Chen, C.-H., Shah, R.K., Abate, A.R. & Weitz, D.A. 2009 Janus particles templated from double emulsion droplets generated using microfluidics. Langmuir 25 (8), 4320–4323.CrossRefGoogle ScholarPubMed
Dean, D.M., Napolitano, A.P., Youssef, J. & Morgan, J.R. 2007 Rods, tori, and honeycombs: the directed self-assembly of microtissues with prescribed microscale geometries. FASEB J. 21 (14), 4005–4012.CrossRefGoogle ScholarPubMed
Deshmukh, S.D. & Thaokar, R.M. 2013 Deformation and breakup of a leaky dielectric drop in a quadrupole electric field. J. Fluid Mech. 731, 713–733.Google Scholar
Ee, B.K., Lavrenteva, O.M., Smagin, I. & Nir, A. 2018 Evolution and stationarity of liquid toroidal drop in compressional stokes flow. J. Fluid Mech. 835, 1–23.CrossRefGoogle Scholar
Fontelos, M.A., Garcia-Garrido, V.J. & Kindelán, U. 2011 Evolution and breakup of viscous rotating drops. SIAM J. Appl. Maths 71 (6), 1941–1964.CrossRefGoogle Scholar
Fragkopoulos, A.A. & Fernández-Nieves, A. 2017 Toroidal-droplet instabilities in the presence of charge. Phys. Rev. E 95 (3), 033122.CrossRefGoogle Scholar
Fragkopoulos, A.A., Pairam, E., Berger, E., Segre, P.N. & Fernández-Nieves, A. 2017 Shrinking instability of toroidal droplets. Proc. Natl Acad. Sci. USA 114 (11), 2871–2875.CrossRefGoogle ScholarPubMed
Ghazian, O., Adamiak, K. & Castle, G.S.P. 2013 Numerical simulation of electrically deformed droplets less conductive than ambient fluid. Colloids Surf. A 423, 27–34.CrossRefGoogle Scholar
Heine, C.-J. 2006 Computations of form and stability of rotating drops with finite elements. IMA J. Numer. Anal. 26 (4), 723–751.CrossRefGoogle Scholar
Hynd, R. & MacCuan, J. 2006 On Toroidal Rotating Drops. Niedersächsische Staats-und Universitätsbibliothek.Google Scholar
Kojima, M., Hinch, E.J. & Acrivos, A. 1984 The formation and expansion of a toroidal drop moving in a viscous fluid. Phys. Fluids 27 (1), 19–32.CrossRefGoogle Scholar
Lavrenteva, O.M., Ee, B.K., Smagin, I. & Nir, A. 2021 Approximating stationary deformation of flat and toroidal drops in compressional viscous flow using generalized Cassini ovals. J. Fluid Mech. 921, A5.CrossRefGoogle Scholar
Machu, G., Meile, W., Nitsche, L. & Schaflinger, U. 2001 a The motion of a swarm of particles travelling through a quiescent, viscous fluid. Z. Angew. Math. Mech. 81 (S3), 547–548.CrossRefGoogle Scholar
Machu, G., Meile, W., Nitsche, L.C. & Schaflinger, U.W.E. 2001 b Coalescence, torus formation and breakup of sedimenting drops: experiments and computer simulations. J. Fluid Mech. 447, 299.CrossRefGoogle Scholar
Malik, S., Lavrenteva, O.M. & Nir, A. 2020 Shapes and stability of viscous rotating drops in a compressional/extensional flow. Phys. Rev. Fluids 5 (2), 023604.CrossRefGoogle Scholar
Mehrabian, H. & Feng, J.J. 2013 Capillary breakup of a liquid torus. J. Fluid Mech. 717, 281.CrossRefGoogle Scholar
Menchaca R, A., Borunda, M., Hidalgo, S.S., Huidobro, F., Michaelian, K., Pérez, A. & Rodríguez, V. 1996 Are the toroidal shapes of heavy-ion reactions seen in macroscopic drop collisions? Revista Mexicana de Fisica 42 (suppl. 1), 198–202.Google Scholar
Nurse, A., Freund, L.B. & Youssef, J. 2012 A model of force generation in a three-dimensional toroidal cluster of cells. J. Appl. Mech. 79 (5), 051013.CrossRefGoogle Scholar
Nurse, A.K., Coriell, S.R. & McFadden, G.B. 2015 On the stability of rotating drops. J. Res. Natl Inst. Stand. Technol. 120, 74–101.CrossRefGoogle ScholarPubMed
Pairam, E. & Fernández-Nieves, A. 2009 Generation and stability of toroidal droplets in a viscous liquid. Phys. Rev. Lett. 102 (23), 234501.CrossRefGoogle Scholar
Pairam, E., Vallamkondu, J., Koning, V., van Zuiden, B.C., Ellis, P.W., Bates, M.A., Vitelli, V. & Fernandez-Nieves, A. 2013 Stable nematic droplets with handles. Proc. Natl Acad. Sci. USA 110 (23), 9295–9300.CrossRefGoogle ScholarPubMed
Plateau, J. 1857 I. Experimental and theoretical researches on the figures of equilibrium of a liquid mass withdrawn from the action of gravity–third series. Lond. Edinb. Dublin Phil. Mag. J. Sci. 14 (90), 1–22.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
Rallison, J.M. & Acrivos, A. 1978 A numerical study of the deformation and burst of a viscous drop in an extensional flow. J. Fluid Mech. 89 (1), 191–200.CrossRefGoogle Scholar
Renardy, Y., Popinet, S., Duchemin, L., Renardy, M., Zaleski, S., Josserand, C., Drumright-Clarke, M.A., Richard, D., Clanet, C. & Quéré, D. 2003 Pyramidal and toroidal water drops after impact on a solid surface.CrossRefGoogle Scholar
Sharma, V., Szymusiak, M., Shen, H., Nitsche, L.C. & Liu, Y. 2012 Formation of polymeric toroidal-spiral particles. Langmuir 28 (1), 729–735.CrossRefGoogle ScholarPubMed
Shum, H.C., Abate, A.R., Lee, D., Studart, A.R., Wang, B., Chen, C.-H., Thiele, J., Shah, R.K., Krummel, A. & Weitz, D.A. 2010 Droplet microfluidics for fabrication of non-spherical particles. Macromol. Rapid Commun. 31 (2), 108–118.CrossRefGoogle ScholarPubMed
Sostarecz, M.C. & Belmonte, A. 2003 Motion and shape of a viscoelastic drop falling through a viscous fluid. J. Fluid Mech. 497, 235–252.CrossRefGoogle Scholar
Szymusiak, M., Sharma, V., Nitsche, L.C. & Liu, Y. 2012 Interaction of sedimenting drops in a miscible solution–formation of heterogeneous toroidal-spiral particles. Soft Matt. 8 (29), 7556–7559.CrossRefGoogle Scholar
Texier, B.D., Piroird, K., Quéré, D. & Clanet, C. 2013 Inertial collapse of liquid rings. J. Fluid Mech. 717.Google Scholar
Zabarankin, M., Lavrenteva, O.M. & Nir, A. 2015 Liquid toroidal drop in compressional Stokes flow. J. Fluid Mech. 785, 372–400.CrossRefGoogle Scholar
Zabarankin, M., Smagin, I., Lavrenteva, O.M. & Nir, A. 2013 Viscous drop in compressional Stokes flow. J. Fluid Mech. 720, 169–191.CrossRefGoogle Scholar