Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gattere, Federica
Chiarini, Alessandro
and
Quadrio, Maurizio
2022.
Dimples for Skin-Friction Drag Reduction: Status and Perspectives.
Fluids,
Vol. 7,
Issue. 7,
p.
240.
Gallorini, Emanuele
Quadrio, Maurizio
and
Gatti, Davide
2022.
Coherent near-wall structures and drag reduction by spanwise forcing.
Physical Review Fluids,
Vol. 7,
Issue. 11,
Ma, Rui
Gao, Zheng-hong
Lu, Lian-shan
and
Chen, Shu-sheng
2022.
Skin-friction drag reduction by local porous uniform blowing in spatially developing compressible turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 12,
Cacciatori, Lorenzo
Brignoli, Carlo
Mele, Benedetto
Gattere, Federica
Monti, Celeste
and
Quadrio, Maurizio
2022.
Drag Reduction by Riblets on a Commercial UAV.
Applied Sciences,
Vol. 12,
Issue. 10,
p.
5070.
Mele, Benedetto
2022.
Riblet Drag Reduction Modeling and Simulation.
Fluids,
Vol. 7,
Issue. 7,
p.
249.
Massaro, Daniele
Martinelli, Fulvio
Schmid, Peter
and
Quadrio, Maurizio
2023.
Linear stability of Poiseuille flow over a steady spanwise Stokes layer.
Physical Review Fluids,
Vol. 8,
Issue. 10,
Lusher, David J.
Zauner, Markus
Sansica, Andrea
and
Hashimoto, Atsushi
2023.
Automatic Code-Generation to Enable High-Fidelity Simulations of Multi-Block Airfoils on GPUs.
Mele, Benedetto
Saetta, Ettore
and
Tognaccini, Renato
2023.
Analysis of riblets modeling for aeronautical applications.
Che, Zheng-Xin
Chen, Zheng-Wei
Ni, Yi-Qing
Huang, Sha
and
Li, Zhi-Wei
2023.
Research on the impact of air-blowing on aerodynamic drag reduction and wake characteristics of a high-speed maglev train.
Physics of Fluids,
Vol. 35,
Issue. 11,
Albers, Marian
Shao, Xiao
and
Schröder, Wolfgang
2024.
Energy efficient actuated drag reduced compressible turbulent flat plate flow.
International Journal of Heat and Fluid Flow,
Vol. 106,
Issue. ,
p.
109314.
Gallorini, Emanuele
and
Quadrio, Maurizio
2024.
Spatial discretization effects in spanwise forcing for turbulent drag reduction.
Journal of Fluid Mechanics,
Vol. 982,
Issue. ,
Lagemann, Esther
Brunton, Steven L.
and
Lagemann, Christian
2024.
Uncovering wall-shear stress dynamics from neural-network enhanced fluid flow measurements.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 480,
Issue. 2292,
Zhao, QingYu
Huang, Jun
Guo, YuXin
Pan, YuXuan
Ji, JingJing
and
Huang, YongAn
2024.
Machine learning-assisted sparse observation assimilation for real-time aerodynamic field perception.
Science China Technological Sciences,
Vol. 67,
Issue. 5,
p.
1458.
Deshpande, Rahul
Kidanemariam, Aman G.
and
Marusic, Ivan
2024.
Pressure drag reduction via imposition of spanwise wall oscillations on a rough wall.
Journal of Fluid Mechanics,
Vol. 979,
Issue. ,
Hou, Jiaxin
Xiao, Xing
Xie, Junlong
and
Chen, Jianye
2024.
Numerical investigation of nitrogen spontaneous condensation over airfoils in cryogenic wind tunnel.
Case Studies in Thermal Engineering,
Vol. 59,
Issue. ,
p.
104524.
Ali, Haris
Rasani, Mohammad Rasidi
Harun, Zambri
and
Shahid, Muhammad Ashhad
2024.
Passive flow-field control using dimples for improved aerodynamic flow over a wing.
Scientific Reports,
Vol. 14,
Issue. 1,
Gattere, Federica
Zanolini, Massimo
Gatti, Davide
Bernardini, Matteo
and
Quadrio, Maurizio
2024.
Turbulent drag reduction with streamwise-travelling waves in the compressible regime.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Berizzi, Niccolò
Gatti, Davide
Soldati, Giulio
Pirozzoli, Sergio
and
Quadrio, Maurizio
2025.
Near-Field Aeroacoustics of Spanwise Forcing on a Transonic Wing: A DNS Study.
Applied Sciences,
Vol. 15,
Issue. 2,
p.
814.
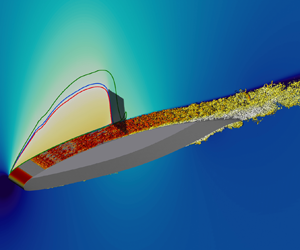
 $Re_\infty = 3 \times 10^{5}$ and
$Re_\infty = 3 \times 10^{5}$ and  $M_\infty =0.7$. Control via spanwise forcing is applied over a fraction of the suction side of the airfoil. Besides locally reducing friction, the control modifies the shock wave and significantly improves the aerodynamic efficiency of the airfoil by increasing lift and decreasing drag. Hence, the airfoil can achieve the required lift at a lower angle of attack and with a lower drag. Estimates at the aircraft level indicate that substantial savings are possible; when control is active, its energy cost becomes negligible thanks to the small application area. We suggest that skin-friction drag reduction should be considered not only as a goal, but also as a tool to improve the global aerodynamics of complex flows.
$M_\infty =0.7$. Control via spanwise forcing is applied over a fraction of the suction side of the airfoil. Besides locally reducing friction, the control modifies the shock wave and significantly improves the aerodynamic efficiency of the airfoil by increasing lift and decreasing drag. Hence, the airfoil can achieve the required lift at a lower angle of attack and with a lower drag. Estimates at the aircraft level indicate that substantial savings are possible; when control is active, its energy cost becomes negligible thanks to the small application area. We suggest that skin-friction drag reduction should be considered not only as a goal, but also as a tool to improve the global aerodynamics of complex flows.


