Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T18:28:37.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Double solution and influence of secondary waves on transition criteria for shock interference in pre-Mach reflection with two incident shock waves

Published online by Cambridge University Press:  29 January 2020

Xiao-Ke Guan ,
Chen-Yuan Bai  and
Zi-Niu Wu Open the ORCID record for Zi-Niu Wu [Opens in a new window]
Xiao-Ke Guan
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing100084, PR China
Chen-Yuan Bai
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing100084, PR China
Zi-Niu Wu*
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing100084, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

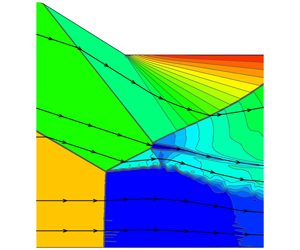
Mach reflection in steady supersonic flow with two incident shock waves that reflect at the same point on the reflecting surface has been studied recently. Under some conditions we have pre-Mach reflection, where the first incident shock wave produces Mach reflection, the reflected shock wave of which intersects the second incident shock wave, leading to a type I shock interference structure. In this study, we find that a critical condition exists to have a double solution of this shock interference, i.e. we may either have type I interference or type II interference. However, numerical simulation shows that, for inverted Mach reflection, the double solution domain is below the theoretical one and for usual Mach reflection, the double solution domain is above the theoretical one. This discrepancy is found to be due to secondary Mach waves on the initial segment of the slipline of the Mach reflection, thus demonstrating for the first time a case where the transition criterion is modified by secondary Mach waves developed over the primary flow structure.

JFM classification

Aerodynamics: High-speed flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 887 , 25 March 2020 , A22
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. D. Jr 2019 Hypersonic and High-Temperature Gas Dynamics, 3rd edn. AIAA Education Series.CrossRefGoogle Scholar
Bai, C. Y. & Wu, Z. N. 2017 Size and shape of shock waves and slipline for Mach reflection in steady flow. J. Fluid Mech. 818, 116–140.CrossRefGoogle Scholar
Ben-Dor, G. 2007 Shock Wave Reflection Phenomena. Springer.Google Scholar
Ben-Dor, G., Elperin, T., Li, H. & Vasiliev, E. 1999 The influence of the downstream pressure on the shock wave reflection phenomenon in steady flows. J. Fluid Mech. 386, 213–232.CrossRefGoogle Scholar
Ben-Dor, G., Ivanov, M., Vasilev, E. I. & Elperin, T. 2002 Hysteresis processes in the regular reflection 2: Mach reflection transition in steady flows. Prog. Aerosp. Sci. 38, 347–387.CrossRefGoogle Scholar
Chen, Z. J., Bai, C. Y. & Wu, Z. N. 2019 Mach reflection in steady supersonic flow considering wedge boundary-layer correction. Chin. J. Aeronaut. (in press) doi:10.1016/j.cja.2019.09.007.CrossRefGoogle Scholar
Gao, B. & Wu, Z. N. 2010 A study of the flow structure for Mach reflection in steady supersonic flow. J. Fluid Mech. 656, 29–50.CrossRefGoogle Scholar
Guan, X. K., Bai, C. Y. & Wu, Z. N. 2018 Steady Mach reflection with two incident shock waves. J. Fluid Mech. 855, 882–909.CrossRefGoogle Scholar
Hekiri, H. & Emanuel, G. 2015 Structure and morphology of a triple point. Phys. Fluids 27, 056102.CrossRefGoogle Scholar
Henderson, L. F. & Lozzi, A. 1975 Experiments on transition of Mach reflection. J. Fluid Mech. 68, 139–155.CrossRefGoogle Scholar
Henderson, L. F. & Lozzi, A. 1979 Further experiments on transition to Mach reflexon. J. Fluid Mech. 94, 541–559.CrossRefGoogle Scholar
Hillier, R. 2007 Shock-wave/expansion-wave interactions and the transition between regular and Mach reflection. J. Fluid Mech. 575, 399–424.CrossRefGoogle Scholar
Hornung, H. G. 1986 Regular and Mach reflections of shock waves. Annu. Rev. Fluid Mech. 18, 33–58.CrossRefGoogle Scholar
Hornung, H. G. 2014 Mach reflection in steady flow. I. Mikhail Ivanov’s contributions, II. Caltech stability experiments. In AIP Conference Proceedings, vol. 1628, pp. 1384–1393. AIP Publishing.Google Scholar
Hornung, H. G., Oertel, H. & Sandeman, R. J. 1979 Transition to Mach reflection of shock waves in steady and pseudo-steady flows with and without relaxation. J. Fluid Mech. 90, 541–560.CrossRefGoogle Scholar
Hornung, H. G. & Robinson, M. L. 1982 Transition from regular to Mach reflection of shock waves. Part 2. The steady-flow criterion. J. Fluid Mech. 123, 155–164.CrossRefGoogle Scholar
Hu, Z. M., Gao, Y. L., Myong, R. S., Dou, H. S. & Khoo, B. C. 2010 Geometric criterion for transition in hypersonic double-wedge flows. Phys. Fluids 22, 016101.CrossRefGoogle Scholar
Hu, Z. M., Kim, M. S., Myong, R. S. & Cho, T. H. 2008 On the RR-MR transition of asymmetric shock waves in steady flows. Shock Waves 18, 419–423.CrossRefGoogle Scholar
Li, H., Chpoun, A. & Ben-Dor, G. 1999 Analytical and experimental investigations of the reflection of asymmetric shock waves in steady flows. J. Fluid Mech. 390, 25–43.CrossRefGoogle Scholar
Li, H. & Ben-Dor, G. 1997 A parametric study of Mach reflection in steady flows. J. Fluid Mech. 341, 101–125.CrossRefGoogle Scholar
Li, J., Zhu, Y. J. & Luo, X. S. 2014 On Type VI–V transition in hypersonic double-wedge flows with thermo-chemical nonequilibrium effects. Phys. Fluids 26, 086104.CrossRefGoogle Scholar
Lin, J., Bai, C. Y. & Wu, Z. N. 2019 Study of asymmetrical whock wave reflection in steady supersonic flow. J. Fluid Mech. 864, 848–875.CrossRefGoogle Scholar
von Neumann, J.1943 Oblique reflection of shock. Explos. Res. Rep. 12. Navy Dept., Bureau of Ordinance, Washington, DC.Google Scholar
von Neumann, J.1945 Refraction, intersection and reflection of shock waves. NAVORD Rep. 203–245. Navy Dept., Bureau of Ordinance, Washington, DC.Google Scholar
Roye, L., Henderson, F. & Menikoff, R. 1998 Triple-shock entropy theorem and its consequences. J. Fluid Mech. 366, 179–210.Google Scholar
Schmisseur, J. D. & Gaitonde, D. V. 2011 Numerical simulation of Mach reflection in steady flows. Shock Waves 21, 499–509.CrossRefGoogle Scholar
Shah, S., Martinez, R., Fernandez, N. & Mourtos, N.2008 Double wedge shockwave interaction flow characterization. Thermal and Fluids Analysis Workshop, TFAWS-08-1033 https://tfaws.nasa.gov/TFAWS08/Proceedings/Papers/TFAWS-08-1033.pdf.Google Scholar
Verma, S. B., Manisankar, C. & Akshara, P. 2015 Control of shock-wave boundary layer interaction using steady micro-jets. Shock Waves 25 (5), 535–543.CrossRefGoogle Scholar
Xiong, W. T., Zhu, Y. J. & Luo, X. S. 2016 On transition of type V interaction in double-wedge flow with non-equilibrium effects. Theoret. Appl. Mech. Lett. 6, 282–285.CrossRefGoogle Scholar