Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T09:01:03.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Dissipation element analysis in turbulent channel flow

Published online by Cambridge University Press:  02 February 2012

Fettah Aldudak  and
Martin Oberlack
Fettah Aldudak*
Affiliation:
Department of Mechanical Engineering, TU Darmstadt, Petersenstrasse 30, 64287 Darmstadt, Germany
Martin Oberlack
Affiliation:
Department of Mechanical Engineering, TU Darmstadt, Petersenstrasse 30, 64287 Darmstadt, Germany Center of Smart Interfaces, TU Darmstadt, Petersenstrasse 32, 64287 Darmstadt, Germany GS Computational Engineering, TU Darmstadt, Dolivostrasse 15, 64293 Darmstadt, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In order to analyse the geometric structure of turbulent flow patterns and their statistics for various scalar fields we adopt the dissipation element (DE) approach and apply it to turbulent channel flow by employing direct numerical simulations (DNS) of the Navier–Stokes equations. Gradient trajectories starting from any point in a scalar field in the directions of ascending and descending scalar gradients will always reach an extremum, i.e. a minimum or a maximum point, where 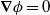. The set of all points and trajectories belonging to the same pair of extremal points defines a dissipation element. Extending previous DE approaches, which were only applied to homogeneous turbulence, we here focus on exploring the influence of solid walls on the dissipation element distribution. Employing group-theoretical methods and known symmetries of Navier–Stokes equations, we observe for the core region of the flow, i.e. the region beyond the buffer layer, that the probability distribution function (p.d.f.) of the DE length exhibits an invariant functional form, in other words, self-similar behaviour with respect to the wall distance. This is further augmented by the scaling behaviour of the mean DE length scale which shows a linear scaling with the wall distance. The known proportionality of the mean DE length and the Taylor length scale is also revisited. Utilizing a geometric analogy we give the number of DE elements as a function of the wall distance. Further, it is observed that the DE p.d.f. is rather insensitive, i.e. invariant with respect both to the Reynolds number and the actual scalar which has been employed for the analysis. In fact, a very remarkable degree of isotropy is observed for the DE p.d.f. in regions of high shear. This is in stark contrast to classical Kolmogorov scaling laws which usually exhibit a strong dependence on quantities such as shear, anisotropy and Reynolds number. In addition, Kolmogorov’s scaling behaviour is in many cases only visible for very large Reynolds numbers. This is rather different in the present DE approach which applies also for low Reynolds numbers. Moreover, we show that the DE p.d.f. agrees very well with the log-normal distribution and derive a log-normal p.d.f. model taking into account the wall-normal dependence. Finally, the conditional mean scalar differences of the turbulent kinetic energy at the extremal points of DE are examined. We present a power law with scaling exponent of 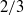known from Kolmogorov’s hypothesis for the centre of the channel and a logarithmic law near the wall.

JFM classification

Waves/Free-surface Flows: Channel flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 332 - 351
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aldudak, F. & Oberlack, O. 2009 Dissipation element analysis of scalar fields in wall-bounded turbulent flow. Proceedings of EUROMECH Colloquium 512: Small Scale Turbulence and Related Gradient Statistics, pp. 9–11.Google Scholar
2. Benzi, R., Amati, G., Casciola, C. M. & Toschi, F. 1999 Intermittency and structure functions in channel flow turbulence. Phys. Fluids 11, 1284.CrossRefGoogle Scholar
3. Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414 (2–3), 43–164.CrossRefGoogle Scholar
4. Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in isotropic turbulence. J. Appl. Phys. 22, 469–473.CrossRefGoogle Scholar
5. Gibson, C. H. 1968 Fine structure of scalar fields mixed by turbulence i. Zero gradient points and minimal gradient surfaces. Phys. Fluids 11, 2305–2315.CrossRefGoogle Scholar
6. Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.CrossRefGoogle Scholar
7. Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133.CrossRefGoogle Scholar
8. Kolmogorov, A. N. 1941 The local structure of turbulence in an incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
9. Lundbladh, A., Berlin, S., Skote, M., Hildings, C., Choi, J., Kim, J. & Henningson, D. S. 1999 An efficient spectral method for simulation of incompressible flow over a flat plate. Tech. Rep. 1999:11. KTH, Stokholm.Google Scholar
10. Oberlack, M. 1999 Similarity in non-rotating and rotating turbulent pipe flows. J. Fluid Mech. 379, 1–22.CrossRefGoogle Scholar
11. Oberlack, M. 2000 Symmetrie, invarianz und selbstähnlichkeit in der turbulenz. Habilitation thesis, RWTH Aachen.Google Scholar
12. Oberlack, M. 2001 A unified approach for symmetries in plane parallel turbulent shear flows. J. Fluid Mech. 427, 299–328.CrossRefGoogle Scholar
13. Oberlack, M. & Rosteck, A. 2010 New statistical symmetries of the multi-point equations and its importance for turbulent scaling laws. Discret. Contin. Dyn. S. 3 (3), 451–471.Google Scholar
14. Obukhov, A. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13, 77–81.CrossRefGoogle Scholar
15. Perry, A. E., Henbest, S. M. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 163, 163–199.CrossRefGoogle Scholar
16. Peters, N. & Wang, L. 2006 Dissipation element analysis of scalar fields in turbulence. C. R. Mech. 334, 493–506.CrossRefGoogle Scholar
17. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
18. Richardson, L. F. 1922 Weather Prediction by Numerical Process, p. xii+236. Cambridge University Press.Google Scholar
19. Rosteck, A. & Oberlack, M. 2011 Lie algebra of the symmetries of the multi-point equations in statistical turbulence theory. J. Nonlinear Math. Phy. 18 (suppl. 1), 251–264.CrossRefGoogle Scholar
20. Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.CrossRefGoogle Scholar
21. Skote, M. 2001 Studies of turbulent boundary layer flow through direct numerical simulation. PhD thesis, Royal Institute of Technology, Stockholm, Sweden.Google Scholar
22. Toschi, F., Amati, G., Succi, S., Benzi, R. & Piva, R. 1999 Intermittency and structure functions in channel flow turbulence. Phys. Rev. Lett. 82 (25), 5044–5047.CrossRefGoogle Scholar
23. Ünal, G. 1994 Application of equivalence transformations to inertial subrange of turbulence. Lie Groups Appl. 1 (1), 232–240.Google Scholar
24. Wang, L. & Peters, N. 2006 The length scale distribution function of the distance between extremal points in passive scalar turbulence. J. Fluid Mech. 554, 457–475.CrossRefGoogle Scholar
25. Wang, L. & Peters, N. 2008 Length-scale distribution functions and conditional means for various fields in turbulence. J. Fluid Mech. 608, 113–138.CrossRefGoogle Scholar