Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T22:24:09.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersion in two-dimensional turbulent buoyant plumes

Published online by Cambridge University Press:  02 June 2015

Stefano Rocco  and
Andrew W. Woods
Stefano Rocco
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using high-resolution imaging and dye studies, we investigate experimentally the mixing of a tracer by the eddies within a two-dimensional turbulent buoyant plume. Instantaneously, the plume consists of a series of eddies, and at each point along the centreline of the plume, the along-plume speed of the leading edge of the eddies 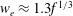$w_{e}\approx 1.3f^{1/3}$, where 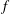$f$ is the buoyancy flux, while the product of the length scale, 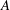$A$, and frequency, 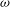${\it\omega}$, of the eddies 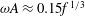${\it\omega}A\approx 0.15f^{1/3}$. The circulation and flow associated with the eddies lead to longitudinal mixing relative to the mean flow. To illustrate this mixing, we analyse the evolution of the horizontally averaged dye front produced by adding a constant flux of dye to a steady plume for times 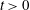$t>0$. We show that the centre of mass of the horizontally averaged dye front has an along-plume speed 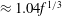${\approx}1.04f^{1/3}$. This is consistent with the predictions of a time-averaged model for the evolution of the horizontally averaged mass, momentum and buoyancy flux in the plume. The new data also show that the longitudinal spreading of the horizontally averaged dye front can be described in terms of a dispersivity 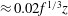${\approx}\,0.02f^{1/3}z$, where $z$ is the vertical distance below the source. This model of longitudinal mixing enables calculation of the residence time distribution of material in the plume, which may be key to modelling the products of a reaction in which the reaction time is comparable to the travel time in the plume.

JFM classification

Mixing: Turbulent mixing
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , R1
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ai, J., Law, A. W.-K. & Yu, S. C. M. 2006 On Boussinesq and non-Boussinesq starting forced plumes. J. Fluid Mech. 558, 357–386.Google Scholar
van den Bremer, T. S. & Hunt, G. R. 2014 Two-dimensional planar plumes and fountains. J. Fluid Mech. 750, 210–244.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2008 On the rise of turbulent plumes: quantitative effects of variable entrainment for submarine hydrothermal vents, terrestrial and extra terrestrial explosive volcanism. J. Geophys. Res. 113 (B9), B09201.Google Scholar
Chen, B. D. & Jirka, G. H. 1999 LIF study of plane jet bounded in shallow water layer. J. Hydraul. Engng 125 (August), 817–826.CrossRefGoogle Scholar
Danckwerts, P. V. 1953 Continuous flow systems, distribution of residence times. Chem. Engng Sci. 2 (1), 1–13.CrossRefGoogle Scholar
Daoyi, C. & Jirka, G. H. 1998 Linear stability analysis of turbulent mixing layers and jets in shallow water layers. J. Hydraul. Res. 36 (5), 815–830.CrossRefGoogle Scholar
Dracos, T., Giger, M. & Jirka, G. H. 1992 Plane turbulent jets in a bounded fluid layer. J. Fluid Mech. 241, 587–614.CrossRefGoogle Scholar
Kotsovinos, N. E. & List, E. J. 1977 Plane turbulent buoyant jets. Part 1. Integral properties. J. Fluid Mech. 81 (1), 25–44.Google Scholar
Landel, J. R., Caulfield, C. P. & Woods, A. W. 2012a Meandering due to large eddies and the statistically self-similar dynamics of quasi-two-dimensional jets. J. Fluid Mech. 692, 347–368.CrossRefGoogle Scholar
Landel, J. R., Caulfield, C. P. & Woods, A. W. 2012b Streamwise dispersion and mixing in quasi-two-dimensional steady turbulent jets. J. Fluid Mech. 711, 212–258.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234 (1196), 1–23.Google Scholar
Paillat, S. & Kaminski, E. 2014 Entrainment in plane turbulent pure plumes. J. Fluid Mech. 755, R2.Google Scholar
Papanicolaou, P. N. & List, E. J. 1988 Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 195 (-1), 341–391.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Prandtl, L. 1925 Bericht uber Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 5 (2), 136–139.Google Scholar
Prandtl, L. 1954 Essentials of Fluid Dynamics. Blackie.Google Scholar
Taylor, G. 1954 The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. Lond. 223, 446–468.Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42 (1), 391–412.Google Scholar
Yih, C.-S. 1977 Turbulent buoyant plumes. Phys. Fluids 20 (8), 1234–1237.Google Scholar