Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-19T09:06:27.808Z Has data issue: false hasContentIssue false
  • English
  • Français

A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow

Published online by Cambridge University Press:  11 July 2008

XIAOHUA WU  and
PARVIZ MOIN
XIAOHUA WU
Affiliation:
Department of Mechanical Engineering, Royal Military College of Canada, Kingston, Ontario, CanadaK7K [email protected]
PARVIZ MOIN
Affiliation:
Center for Turbulence Research, Stanford University, Stanford CA 94305–3035, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fully developed incompressible turbulent pipe flow at bulk-velocity- and pipe-diameter-based Reynolds number ReD=44000 was simulated with second-order finite-difference methods on 630 million grid points. The corresponding Kármán number R+, based on pipe radius R, is 1142, and the computational domain length is 15R. The computed mean flow statistics agree well with Princeton Superpipe data at ReD=41727 and at ReD=74000. Second-order turbulence statistics show good agreement with experimental data at ReD=38000. Near the wall the gradient of 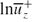with respect to ln(1−r)+ varies with radius except for a narrow region, 70 < (1−r)+ < 120, within which the gradient is approximately 0.149. The gradient of 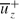with respect to ln{(1−r)++a+} at the present relatively low Reynolds number of ReD=44000 is not consistent with the proposition that the mean axial velocity 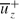is logarithmic with respect to the sum of the wall distance (1−r)+ and an additive constant a+ within a mesolayer below 300 wall units. For the standard case of a+=0 within the narrow region from (1−r)+=50 to 90, the gradient of 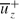with respect to ln{(1−r)++a+} is approximately 2.35. Computational results at the lower Reynolds number ReD=5300 also agree well with existing data. The gradient of 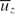with respect to 1−r at ReD=44000 is approximately equal to that at ReD=5300 for the region of 1−r > 0.4. For 5300 < ReD < 44000, bulk-velocity-normalized mean velocity defect profiles from the present DNS and from previous experiments collapse within the same radial range of 1−r > 0.4. A rationale based on the curvature of mean velocity gradient profile is proposed to understand the perplexing existence of logarithmic mean velocity profile in very-low-Reynolds-number pipe flows. Beyond ReD=44000, axial turbulence intensity varies linearly with radius within the range of 0.15 < 1−r < 0.7. Flow visualizations and two-point correlations reveal large-scale structures with comparable near-wall azimuthal dimensions at ReD=44000 and 5300 when measured in wall units. When normalized in outer units, streamwise coherence and azimuthal dimension of the large-scale structures in the pipe core away from the wall are also comparable at these two Reynolds numbers.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 608 , 10 August 2008 , pp. 81 - 112
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akselvoll, K. & Moin, P. 1996 a Large eddy simulation of confined turbulent coaxial jets. J. Fluid Mech. 315, 387–411.CrossRefGoogle Scholar
Akselvoll, K. & Moin, P. 1996 b An efficient method for temporal integration of the Navier–Stokes equations in confined axisymmetric geometries. J. Comput. Phys. 125, 454–463.CrossRefGoogle Scholar
Bailey, S., Hultmark, M., Smits, A. J. & Schultz, M. 2007 Azimuthal correlation in the outer layer of turbulent pipe flow. Bull. Am. Phys. Soc. 52, 24.Google Scholar
Barenblatt, G. I. & Chorin, A. J. 1998 Scaling of the intermediate region in wall-bounded turbulence: The power law. Phys. Fluids 10, 1043–1044.CrossRefGoogle Scholar
Barenblatt, G. I., Chorin, A. J. & Prostokishin, V. M. 1997 Scaling laws for fully developed turbulent flow in pipes. Appl. Mech. Rev. 50, 413–529.CrossRefGoogle Scholar
Durst, F., Jovanovic, J. & Sender, J. 1995 LDA measurements in the near-wall region of a turbulent pipe flow. J. Fluid Mech. 295, 305–335. Data available at http://torroja.dmt.upm.es/ftp/AGARD/.CrossRefGoogle Scholar
Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M.. 1994 Fully developed turbulent pipe flow: A comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–209.CrossRefGoogle Scholar
Fukagata, K. & Kasagi, N. 2002 Highly energy-conservative finite difference method for the cylindrical coordinate system. J. Comput. Phys. 181, 478–498.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow, J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hinze, J. O. 1975 Turbulence. Second edition. McGraw-Hill.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Reτ=2003 Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very-large scale motion in the outer layer. Phys. Fluids 11, 417–422.CrossRefGoogle Scholar
Lawn, C. J. 1971 The determination of the rate of dissipation in turbulent pipe flow. J. Fluid Mech. 48, 477–505.CrossRefGoogle Scholar
Loulou, P., Moser, R. D., Mansour, N. N. & Cantwell, B. J. 1997 Direct numerical simulation of incompressible pipe flow using a B-spline spectral method. NASA Technical Memo. Data available at http://torroja.dmt.upm.es/ftp/AGARD/.Google Scholar
McKeon, B. J., Li, J., Jiang, W., Morrison, J. F. & Smits, A. J. 2004 a Further observations on the mean velocity distribution in fully developed pipe flow. J. Fluid Mech. 501, 135–147.CrossRefGoogle Scholar
McKeon, B. J., Swanson, C. J., Zagarola, M. V., Donnelly, R. J. & Smits, A. J. 2004 b Friction factors for smooth pipe flow. J. Fluid Mech. 511, 41–44.CrossRefGoogle Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.CrossRefGoogle Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.CrossRefGoogle Scholar
Oberlack, M. 2001 A unified approach for symmetries in plane parallel turbulent shear flows. J. Fluid Mech. 427, 299–328.CrossRefGoogle Scholar
Orlandi, P. & Fatica, M. 1997 Direct simulations of turbulent flow in a pipe rotating about its axis. J. Fluid Mech. 343, 43–72.CrossRefGoogle Scholar
Perry, A. E., Hafez, S. & Chong, M. S. 2001 A possible reinterpretation of the Princeton Superpipe data. J. Fluid Mech. 439, 395–401.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. M. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Pierce, C. D. & Moin, P. 2001 Progress variable approach for large-eddy simulation of turbulent combustion. Repo. TF-80, Stanford University.Google Scholar
Pierce, C. D. & Moin, P. 2004 Progress variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech., 504, 73–97.CrossRefGoogle Scholar
Satake, S., Kunugi, T. & Himeno, R. 2000 High Reynolds number computation for turbulent heat transfer in a pipe flow. In Lecture Notes in Computer Science, pp. 514–523. Springer.Google Scholar
Smits, A. J. & Zagarola, M. V. 1998 Response to ‘Scaling of the intermediate region in wall-bounded turbulence: The power law’. Phys. Fluids 10, 1045–1046.CrossRefGoogle Scholar
Toonder, J. M. J. & Nieuwstadt, F. T. M. 1997 Reynolds number effects in a turbulent pipe flow for low to moderate Re. Phys. Fluids 9, 3401–3409.Google Scholar
Veenman, M. P. B. 2004 Statistical analysis of turbulent pipe flow: numerical approach. Ph.D. thesis, Eindhoven University of Technology, Faculty of Mechanical Engineering.Google Scholar
Wagner, C., Huttl, T. J. & Friedrich, R. 2001 Low Reynolds number effects derived from direct numerical simulations of turbulent pipe flow. Comput. Fluids 30, 581–590.CrossRefGoogle Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Wosnik, W., Castillo, L. & George, W. K. 2000 A theory for turbulent pipe and channel flows. J. Fluid Mech. 421, 115–145.CrossRefGoogle Scholar
Wu, X., Schluter, J., Moin, P., Pitsch, H., Iaccarino, G. & Ham, F. 2006 Computational study on the internal layer in a diffuser. J. Fluid Mech. 550, 391–412.CrossRefGoogle Scholar
Zagarola, M. V., Perry, A. E. & Smits, A. J. 1997 Log laws or power laws: The scaling in the overlap region. Phys. Fluids 9, 2094–2100.CrossRefGoogle Scholar
Zagarola, M. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar