Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T06:55:30.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of top-down and bottom-up diffusion in the convective boundary layer

Published online by Cambridge University Press:  30 April 2013

Scott B. Waggy ,
Sedat Biringen  and
Peter P. Sullivan
Scott B. Waggy
Affiliation:
Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO 80309, USA
Sedat Biringen*
Affiliation:
Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO 80309, USA
Peter P. Sullivan
Affiliation:
National Center for Atmospheric Research, Boulder, CO 80307, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A direct numerical simulation (DNS) of an unstably stratified convective boundary layer with system rotation was performed to study top-down and bottom-up diffusion processes. In order to better understand near-wall dynamics associated with scalar diffusion in the absence of surface roughness, direct simulation is utilized to numerically integrate the governing equations that model the atmospheric boundary layer. The ratio of the inversion height to Obukhov length scale, 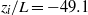${z}_{i} / L= - 49. 1$, indicates moderately strong heating for the case studied. Two passive scalars were initialized in the flow field: the first with a zero gradient at the wall (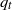${q}_{t} $, top-down diffusion), and the second with a non-zero wall gradient and a close-to-zero gradient at the height of the temperature inversion (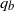${q}_{b} $, bottom-up diffusion). Scalar flux, variance and covariance profiles show good agreement between the DNS and rough-wall large-eddy simulation (LES). The top-down gradient function displays a slight increase in amplitude, indicating reduced mixing efficiency for the smooth-wall, low-Reynolds-number convective boundary layer. For the bottom-up process, the gradient matches other rough-wall simulations. The only notable difference between the smooth-wall DNS data and other rough-wall simulations is an increase in the gradient function near the wall. This indicates that the bottom-up gradient functions for a rough wall and a smooth wall are nearly identical except as the viscous sublayer is approached. Finally, a new empirical model for the scalar variance of a bottom-up scalar is proposed: here, a single function replaces two piecewise relationships to accurately capture the DNS results up to the viscous sublayer. The scalar covariance between top-down and bottom-up processes agrees with rough-wall and tree-canopy LES results; this indicates that the scalar covariance is independent of both Reynolds number and surface friction.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 581 - 606
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Ferreira, R. T. D. S. & Boberg, T. 1986 Turbulent thermal convection in wide horizontal fluid layers. Exp. Fluids 4, 121–141.Google Scholar
Anderson, D. A., Tannehill, J. C. & Pletcher, R. H. 1984 Computational Fluid Mechanics and Heat Transfer. Hemisphere.Google Scholar
Coleman, G. N. & Ferziger, J. H. 1994 A numerical study of the convective boundary layer. Boundary-Layer Meteorol. 70, 247–272.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1990 A numerical study of the Ekman layer. J. Fluid Mech. 213, 313–348.Google Scholar
Deardorff, J. W. 1972 Numerical investigation of neutral and unstable planetary boundary layers. J. Atmos. Sci. 29, 91–115.2.0.CO;2>CrossRefGoogle Scholar
Deardorff, J. W. & Willis, G. E. 1985 Further results from a laboratory model of the convective planetary boundary layer. Boundary-Layer Meteorol. 32, 205–236.Google Scholar
Dhruva, B., Tsuji, Y. & Sreenivasan, K. S. 1997 Transverse structure functions in high-Reynolds-number turbulence. Phys. Rev. E 56 (5), 4928–4930.Google Scholar
Gryanik, V. M. & Hartmann, J. 2002 A turbulence closure for the convective boundary layer based on a two-scale mass-flux approach. J. Atmos. Sci. 59, 2729–2744.2.0.CO;2>CrossRefGoogle Scholar
Jonker, H. J. J., Sullivan, P. P., Patton, E. G. & van Reeuwijk, M. 2010 Direct numerical simulation of entrainment in dry convective boundary layers. In Proceedings of the 19th Symposium on Boundary Layers and Turbulence, Keystone, CO. American Meteorological Society.Google Scholar
LeMone, M. A. 1973 The structure and dynamics of horizontal roll vortices in the planetary boundary layer. J. Atmos. Sci. 30, 1077–1091.Google Scholar
LeMone, M. A. 1990 Some observations of vertical velocity skewness in the convective boundary layer. J. Atmos. Sci. 47, 1163–1169.Google Scholar
Lenschow, D. H., Lothon, M., Mayor, S. D., Sullivan, P. P. & Canut, G. 2012 A comparison of higher-order vertical velocity moments in the convective boundary layer from lidar with in situ measurements and large-eddy simulation. Boundary-Layer Meteorol. 143, 107–123.Google Scholar
Marlatt, S., Waggy, S. & Biringen, S. 2010 Direct numerical simulation of the turbulent Ekman layer: turbulent energy budgets. J. Thermophys. Heat Transfer 24, 544–555.Google Scholar
Marlatt, S., Waggy, S. & Biringen, S. 2012 Direct numerical simulation of the turbulent Ekman layer: evaluation of closure models. J. Atmos. Sci. 69, 1106–1117.Google Scholar
Mason, P. J. 1989 Large-eddy simulation of the convective atmospheric boundary layer. J. Atmos. Sci. 46 (11), 1492–1516.Google Scholar
Mironov, D. V., Gryanik, V. M., Moeng, C. H., Olbers, D. J. & Warncke, T. H. 2000 Vertical turbulence structure and second-moment budgets in convection with rotation: a large-eddy simulation study. Q. J. R. Meteorol. Soc. 126 (563), 477–515.Google Scholar
Miyashita, K., Iwamoto, K. & Kawamura, H. 2006 Direct numerical simulation of the neutrally stratified turbulent Ekman boundary layer. J. Earth Simulator 6, 3–15.Google Scholar
Moene, A. F., Michels, B. I. & Holtslag, A. A. M. 2006 Scaling variances of scalars in a convective boundary layer under different entrainment regimes. Boundary-Layer Meteorol. 120, 257–274.Google Scholar
Moeng, C. H. & Rotunno, R. 1990 Vertical-velocity skewness in the buoyancy-driven boundary layer. J. Atmos. Sci. 47, 1149–1162.Google Scholar
Moeng, C. H. & Wyngaard, J. C. 1984 Statistics of conservative scalars in the convective boundary layers. J. Atmos. Sci. 41, 3161–3169.2.0.CO;2>CrossRefGoogle Scholar
Moeng, C. H. & Wyngaard, J. C. 1988 Spectral analysis of large-eddy simulations of the convective boundary layer. J. Atmos. Sci. 45, 3573–3587.2.0.CO;2>CrossRefGoogle Scholar
Moeng, C. H. & Wyngaard, J. C. 1989 Evaluation of turbulent transport and dissipation closures in second-order modelling. J. Atmos. Sci. 46, 2311–2330.Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.Google Scholar
Obukhov, A. M. 1971 Turbulence in an atmosphere with a non-uniform temperature. Boundary-Layer Meteorol. 2, 7–29.Google Scholar
Patton, E. G., Sullivan, P. P. & Davis, K. J. 2003 The influence of a forest canopy on top-down and bottom-up diffusion in the planetary boundary layer. Q. J. R. Meteorol. Soc. 129, 1415–1434.Google Scholar
Piper, M., Wyngaard, J. C., Snyder, W. H. & Lawson, R. E. Jr. 1995 Top-down, bottom-up diffusion experiments in a water convection tank. J. Atmos. Sci. 52, 3607–3619.Google Scholar
Schmidt, H. & Schumann, U. 1989 Coherent structure of the convective boundary layer derived from large-eddy simulations. J. Fluid Mech. 200, 511–562.Google Scholar
Sorbjan, Z. 2004 Large-eddy simulations of the baroclinic mixed layer. Boundary-Layer Meteorol. 112, 57–80.CrossRefGoogle Scholar
Spalart, P. R., Coleman, G. N. & Johnstone, R. 2008 Direct numerical simulation of the Ekman layer: a step in Reynolds number, and cautious support for a log law with a shifted origin. Phys. Fluids 20, 101507.Google Scholar
Sullivan, P. P., Moeng, C. H., Stevens, B., Lenschow, D. H. & Mayor, S. D. 1998 Stucture of the entrainment zone capping the convective atmospheric boundary layer. J. Atmos. Sci. 55, 3042–3064.Google Scholar
Sullivan, P. P. & Patton, E. G. 2011 The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. J. Atmos. Sci. 68, 2395–2415.Google Scholar
Waggy, S. B. 2012 Turbulent transport in the atmospheric boundary layer with application to wind farm dynamics. PhD thesis, University of Colorado, Boulder, CO.Google Scholar
Waggy, S. B., Kucala, A. M. & Biringen, S. 2012 Parallel implementation of a Navier–Stokes solver: turbulent Ekman layer direct numerical simulation. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, AIAA-2012-0443.Google Scholar
Waggy, S. B., Marlatt, S. & Biringen, S. 2011 Direct numerical simulation of the turbulent Ekman layer: instantaneous flow structures. J. Thermophys. Heat Transfer 25, 309–318.Google Scholar
Wang, W., Davis, K. J., Yi, C., Patton, E. G., Butler, M. P., Ricciuto, D. M. & Bakwin, P. S. 2007 A note on the top-down and bottom-up gradient functions over a forested site. Boundary-Layer Meteorol. 124, 305–314.Google Scholar
Willis, G. E. & Deardorff, J. W. 1974 A laboratory model of the unstable planetary boundary layer. J. Atmos. Sci. 31, 1297–1307.Google Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere, p. 49. Cambridge University Press.Google Scholar
Wyngaard, J. C. & Brost, R. A. 1984 Top-down and bottom-up diffusion of a scalar in the convective boundary layer. J. Atmos. Sci. 41, 102–112.Google Scholar
Zikanov, O., Slinn, D. N. & Dhanak, M. R. 2003 Large-eddy simulations of the wind-induced turbulent Ekman layer. J. Fluid Mech. 495, 343–368.Google Scholar