Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T07:04:46.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of stratified flow past a sphere at a subcritical Reynolds number of 3700 and moderate Froude number

Published online by Cambridge University Press:  02 August 2017

Anikesh Pal ,
Sutanu Sarkar Open the ORCID record for Sutanu Sarkar [Opens in a new window] ,
Antonio Posa  and
Elias Balaras Open the ORCID record for Elias Balaras [Opens in a new window]
Anikesh Pal
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
Sutanu Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
Antonio Posa
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, Washington DC 20052, USA
Elias Balaras
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, Washington DC 20052, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation of flow past a sphere in a stratified fluid is carried out at a subcritical Reynolds number of 3700 and 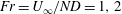$Fr=U_{\infty }/ND=1,2$ and 3 to understand the dynamics of moderately stratified flows with 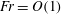$Fr=O(1)$. Here, 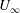$U_{\infty }$ is the free stream velocity, 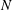$N$ is the background buoyancy frequency and 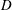$D$ is the sphere diameter. The unstratified flow past the sphere consists of a separated shear layer that transitions to turbulence, a recirculation zone and a wake with a mean centreline deficit velocity, $U_{0}$, that decreases with downstream distance as a power law. With increasing stratification, the separated shear layer plunges inward vertically and its roll up is inhibited, the recirculation zone is shortened and the mean wake decays at a slower rate of 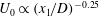$U_{0}\propto (x_{1}/D)^{-0.25}$ in the non-equilibrium (NEQ) region. The transition from the near wake where 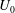$U_{0}$ has a decay rate similar to the unstratified case to the NEQ regime occurs as an oscillatory modulation by a steady lee wave pattern with a period of 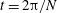$t=2\unicode[STIX]{x03C0}/N$ that leads to accelerated 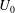$U_{0}$ between 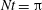$Nt=\unicode[STIX]{x03C0}$ and approximately 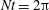$Nt=2\unicode[STIX]{x03C0}$. Far downstream, the wake is dominated by coherent horizontal motions. The acceleration of 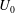$U_{0}$ by the lee wave and the lower turbulence production in the NEQ regime, thereby less loss to turbulence, prolongs the lifetime of the wake relative to its unstratified counterpart. The intensity, temporal spectra and structure of turbulent fluctuations in the wake are assessed. Buoyancy induces significant anisotropy among the velocity components and between their vertical and horizontal profiles. Consequently, the near wake (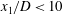$x_{1}/D<10$) exhibits significant differences in turbulence profiles relative to its unstratified counterpart. Spectra of vertical velocity show a discrete peak in the near wake that is maintained further downstream. The turbulent kinetic energy (TKE) balance is computed and contributions from pressure transport and buoyancy are found to become increasingly important as stratification increases. The findings of this investigation will be helpful in designing accurate initial conditions for the temporally evolving model of stratified wakes.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence simulation Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 5 - 31
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdilghanie, A. M. & Diamessis, P. J. 2013 The internal gravity wave field emitted by a stably stratified turbulent wake. J. Fluid Mech. 720, 104–139.Google Scholar
Balaras, E. 2004 Modeling complex boundaries using an external force field on fixed Cartesian grids in large-eddy simulations. Comput. Fluids 33 (3), 375–404.Google Scholar
Bazilevs, Y., Yan, J., de Stadler, M. & Sarkar, S. 2014 Computation of the flow over a sphere at Re = 3700: a comparison of uniform and turbulent inflow conditions. Trans. ASME J. Appl. Mech. 81 (12), 121003.Google Scholar
Bevilaqua, P. M. & Lykoudis, P. S. 1978 Turbulence memory in self-preserving wakes. J. Fluid Mech. 89 (3), 589–606.Google Scholar
Bonneton, P., Chomaz, J. M., Hopfinger, E. & Perrier, M. 1996 The structure of the turbulent wake and the random internal wave field generated by a moving sphere in a stratified fluid. Dyn. Atmos. Oceans 23 (1), 299–308.Google Scholar
Bonneton, P., Chomaz, J. M. & Hopfinger, E. J. 1993 Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 23–40.Google Scholar
Bonnier, M. & Eiff, O. 2002 Experimental investigation of the collapse of a turbulent wake in a stably stratified fluid. Phys. Fluids 14 (2), 791–801.Google Scholar
Brandt, A. & Rottier, J. R. 2015 The internal wavefield generated by a towed sphere at low Froude number. J. Fluid Mech. 769, 109–129.Google Scholar
Brucker, K. A. & Sarkar, S. 2010 A comparative study of self-propelled and towed wakes in a stratified fluid. J. Fluid Mech. 652, 373–404.Google Scholar
Chen, C. C., Gibson, C. H. & Lin, S. C. 1968 Measurements of turbulent velocity and temperature fluctuations in the wake of a sphere. AIAA J. 6, 642–649.Google Scholar
Chomaz, J. M., Bonneton, P., Butet, A., Perrier, M. & Hopfinger, E. J. 1992 Froude number dependence of the flow separation line on a sphere towed in a stratified fluid. Phys. Fluids A 4 (2), 254–258.Google Scholar
Chomaz, J. M., Bonneton, P. & Hopfinger, E. J. 1993a The structure of the near wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 1–21.Google Scholar
Chongsiripinyo, K., Pal, A. & Sarkar, S. 2016 On the vortex dynamics of flow past a sphere at Re = 3700 in a uniformly stratified fluid. Phys. Fluids 29, 020704.Google Scholar
Constantinescu, G. S. & Squires, K. D. 2003 LES and DES investigations of turbulent flow over a sphere at Re = 10 000. Flow Turbul. Combust. 70 (1–4), 267–298.Google Scholar
Dairay, T., Obligado, M. & Vassilicos, J. C. 2015 Non-equilibrium scaling laws in axisymmetric turbulent wakes. J. Fluid Mech. 781, 166–195.Google Scholar
Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R. 2013 Ten Chapters in Turbulence. Cambridge University Press.Google Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, J. A. 2011 Similarity scaling and vorticity structure in high Reynolds number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95.Google Scholar
Dommermuth, D. G., Rottman, J. W., Innis, G. E. & Novikov, E. A. 2002 Numerical simulation of the wake of a towed sphere in a weakly stratified fluid. J. Fluid Mech. 473, 83–101.CrossRefGoogle Scholar
George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. In Advances in Turbulence (ed. George, W. K. & Arndt, R.), pp. 39–73. Hemisphere.Google Scholar
Gilreath, H. E. & Brandt, A. 1985 Experiments on the generation of internal waves in a stratified fluid. AIAA J. 23 (5), 693–700.Google Scholar
Gourlay, M. J., Arendth, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modeling of initially turbulent wakes with net momentum. Phys. Fluids 13, 3783–3802.Google Scholar
Hanazaki, H. 1988 A numerical study of three-dimensional stratified flow past a sphere. J. Fluid Mech. 192, 393–419.Google Scholar
Hopfinger, E. J., Flor, J. B., Chomaz, J. M. & Bonneton, P. 1991 Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp. Fluids 11 (4), 255–261.Google Scholar
Hunt, J. C. R. & Snyder, W. H. 1980 Experiments on stably and neutrally stratified flow over a model three-dimensional hill. J. Fluid Mech. 96, 671–704.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation. Phys. Fluids 31 (11), 3260–3265.Google Scholar
Lin, J. T. & Pao, Y. H. 1979 Wakes in stratified fluids. Annu. Rev. Fluid Mech. 11, 317–338.CrossRefGoogle Scholar
Lin, Q., Boyer, D. L. & Fernando, H. J. S. 1992a Turbulent wakes of linearly stratified flow past a sphere. Phys. Fluids A 4 (8), 1687–1696.Google Scholar
Lin, Q., Lindberg, W. R., Boyer, D. L. & Fernando, H. J. S. 1992b Stratified flow past a sphere. J. Fluid Mech. 240, 315–354.CrossRefGoogle Scholar
Meunier, P., Diamessis, P. J. & Spedding, G. R. 2006 Self-preservation in stratified momentum wakes. Phys. Fluids 18 (10), 106601.Google Scholar
Nedić, J., Vassilicos, J. C. & Ganapathisubramani, B. 2013 Axisymmetric turbulent wakes with new nonequilibrium similarity scalings. Phys. Rev. Lett. 111 (14), 144503.Google Scholar
Orr, T. S., Domaradzki, J. A., Spedding, G. R. & Constantinescu, G. S. 2015 Numerical simulations of the near wake of a sphere moving in a steady, horizontal motion through a linearly stratified fluid at Re = 1000. Phys. Fluids 27 (3), 035113.Google Scholar
Pal, A.2016 Dynamics of stratified flow past a sphere: simulations using temporal, spatial and body inclusive numerical models. PhD thesis, University of California, San Diego, CA.Google Scholar
Pal, A., de Stadler, M. B. & Sarkar, S. 2013 The spatial evolution of fluctuations in a self-propelled wake compared to a patch of turbulence. Phys. Fluids 25, 095106.Google Scholar
Pal, A. & Sarkar, S. 2015 Effect of external turbulence on the evolution of a wake in stratified and unstratified environments. J. Fluid Mech. 772, 361–385.Google Scholar
Pal, A., Sarkar, S., Posa, A. & Balaras, E. 2016 Regeneration of turbulent fluctuations in low-Froude-number flow over a sphere at a Reynolds number of 3700. J. Fluid Mech. 804, R2.Google Scholar
Pasquetti, R. 2011 Temporal/spatial simulation of the stratified far wake of a sphere. Comput. Fluids 40 (1), 179–187.Google Scholar
Redford, J. A., Lund, T. S. & Coleman, G. N. 2015 A numerical study of a weakly stratified turbulent wake. J. Fluid Mech. 776, 568–609.Google Scholar
Rodriguez, I., Borelli, Y., Lehmkuhl, O., Perez Segarra, C. D. & Oliva, A. 2011 Direct numerical simulation of the flow over a sphere at Re = 3700. J. Fluid Mech. 679, 263–287.Google Scholar
Rossi, T. & Toivanen, J. 1999 A parallel fast direct solver for block tridiagonal systems with separable matrices of arbitrary dimension. SIAM J. Sci. Comput. 20 (5), 1778–1793.Google Scholar
Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. J. Fluid Engng 112 (4), 386–392.Google Scholar
Schlichting, H. 1968 Boundary-layer Theory, 7th edn. McGraw-Hill.Google Scholar
Seidl, V., Muzaferija, S. & Perić, M. 1997 Parallel DNS with local grid refinement. Appl. Sci. Res. 59 (4), 379–394.Google Scholar
Spedding, G. R. 1997 The evolution of initially turbulent bluff-body wakes at high internal Froude number. J. Fluid Mech. 337, 283–301.Google Scholar
Spedding, G. R. 2014 Wake signature detection. Annu. Rev. Fluid Mech. 46, 273–302.CrossRefGoogle Scholar
Spedding, G. R., Browand, F. K., Bell, R. & Chen, J. 2000 Internal waves from intermediate, or late-wake vortices. In Stratified Flows I Fifth International Symposium (ed. Pieters, R., Yonemitsu, N. & Lawrence, G. A.), vol. 1, pp. 113–118. University of British Columbia.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.Google Scholar
de Stadler, M. B., Rapaka, N. R. & Sarkar, S. 2014 Large eddy simulation of the near to intermediate wake of a heated sphere at Re = 10 000. Intl J. Heat Fluid Flow 49, 2–10.Google Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar
Uberoi, M. S. & Freymuth, P. 1970 Turbulent energy balance and spectra of axisymmetric wake. Phys. Fluids 13 (9), 2205–2210.Google Scholar
Voisin, B. 1991 Internal wave generation in uniformly stratified fluids. Part 1. Green’s function and point sources. J. Fluid Mech. 231, 439–480.Google Scholar
Voisin, B. 1994 Internal wave generation in uniformly stratified fluids. Part 2. Moving point sources. J. Fluid Mech. 261, 333–374.Google Scholar
Voisin, B. 2007 Lee waves from a sphere in a stratified flow. J. Fluid Mech. 574, 273–315.Google Scholar
Watanabe, T., Riley, J. J., de Bruyn Kops, S. M., Diamessis, P. J. & Zhou, Q. 2016 Turbulent/non-turbulent interfaces in wakes in stably stratified fluids. J. Fluid Mech. 797, R1.CrossRefGoogle Scholar
Yang, J. & Balaras, E. 2006 An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries. J. Comput. Phys. 215 (1), 12–40.Google Scholar
Yun, G., Kim, D. & Choi, H. 2006 Vortical structures behind a sphere at subcritical Reynolds numbers. Phys. Fluids 18 (1), 5102.Google Scholar
Zhou, Q. & Diamessis, P. J. 2016 Surface manifestation of internal waves emitted by submerged localized stratified turbulence. J. Fluid Mech. 798, 505–539.Google Scholar