Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T05:08:43.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of high-speed transition due to an isolated roughness element

Published online by Cambridge University Press:  09 May 2014

Pramod K. Subbareddy ,
Matthew D. Bartkowicz  and
Graham V. Candler
Pramod K. Subbareddy*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, 110 Union Street SE, Minneapolis, MN 55455, USA
Matthew D. Bartkowicz
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, 110 Union Street SE, Minneapolis, MN 55455, USA
Graham V. Candler
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, 110 Union Street SE, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the transition of a Mach 6 laminar boundary layer due to an isolated cylindrical roughness element using large-scale direct numerical simulations (DNS). Three flow conditions, corresponding to experiments conducted at the Purdue Mach 6 quiet wind tunnel are simulated. Solutions are obtained using a high-order, low-dissipation scheme for the convection terms in the Navier–Stokes equations. 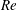The lowest Reynolds number ($Re$) case is steady, whereas the two higher 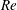$Re$ cases break down to a quasi-turbulent state. Statistics from the highest 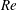$Re$ case show the presence of a wedge of fully developed turbulent flow towards the end of the domain. The simulations do not employ forcing of any kind, apart from the roughness element itself, and the results suggest a self-sustaining mechanism that causes the flow to transition at a sufficiently large Reynolds number. Statistics, including spectra, are compared with available experimental data. Visualizations of the flow explore the dominant and dynamically significant flow structures: the upstream shock system, the horseshoe vortices formed in the upstream separated boundary layer and the shear layer that separates from the top and sides of the cylindrical roughness element. Streamwise and spanwise planes of data were used to perform a dynamic mode decomposition (DMD) (Rowley et al., J. Fluid Mech., vol. 641, 2009, pp. 115–127; Schmid, J. Fluid Mech., vol. 656, 2010, pp. 5–28).

JFM classification

Compressible Flows: Compressible boundary layers Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 848 - 878
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acarlar, M. S. & Smith, C. R. 1987 A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Bagheri, S. 2013 Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596–623.Google Scholar
Baker, C. J. 1979 The laminar horseshoe vortex. J. Fluid Mech. 95, 347–367.Google Scholar
Ballio, F., Bettoni, C. & Franzetti, S. 1998 A survey of time-averaged characteristics of laminar and turbulent horseshoe vortices: (data bank contribution). Trans. ASME: J. Fluids Engng 120 (2), 233–242.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2012 Compressibility effects on roughness-induced boundary layer transition. Intl J. Heat Fluid Flow 35, 45–51.Google Scholar
Chang, C.-L., Choudhari, M. M. & Li, F.2010 Numerical computations of hypersonic boundary-layer over surface irregularities. AIAA Paper 2010-1572.Google Scholar
Chen, K. K., Tu, J. H. & Rowley, C. W. 2012 Variants of dynamic mode decomposition: boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 22 (6), 887–915.Google Scholar
Danehy, P. M., Bathel, B., Ivey, C., Inman, J. A. & Jones, S. B.2009 NO PLIF study of hypersonic transition over a discrete hemispherical roughness element. AIAA Paper 2009-394.Google Scholar
Danehy, P. M., Ivey, C. B., Inman, J. A., Bathel, B. F., Jones, S. B., Jiang, N., Webster, M., Lempert, W., Miller, J. & Meyer, T.2010 High-speed PLIF imaging of hypersonic transition over discrete cylindrical roughness. AIAA Paper 2010-703.Google Scholar
Dolling, D. S. & Bogdonoff, S. M. 1982 Blunt fin-induced shock wave/turbulent boundary-layer interaction. AIAA J. 20 (12), 1674–1680.Google Scholar
van Driest, E. R. 1956 On turbulent flow near a wall. J. Aeronaut. Sci. 23 (11), 1007–1011.CrossRefGoogle Scholar
van Driest, E. R. & Blumer, C. B. 1962 Boundary-layer transition at supersonic speeds – three-dimensional roughness effects (spheres). J. Aero. Sci. 29, 909–916.Google Scholar
Duan, L., Beekman, I. & Martin, M. P. 2010 Direct numerical simulation of hypersonic turbulent boundary layers. Part 2. Effect of wall temperature. J. Fluid Mech. 655, 419–445.Google Scholar
Ducros, F., Ferrand, V., Nicoud, F., Weber, C., Darracq, D., Gacherieu, C. & Poinsot, T. 1999 Large-eddy simulation of shock/turbulence interaction. J. Comput. Phys. 152, 517–549.Google Scholar
Ducros, F., Laporte, F., Souleres, T., Guinot, V., Moinat, P. & Caruelle, B. 2000 High-order fluxes for conservative skew-symmetric-like schemes in structured meshes: application to compressible flows. J. Comput. Phys. 161 (1), 114–139.CrossRefGoogle Scholar
Ergin, F. G. & White, E. B. 2006 Unsteady and transitional flows behind roughness elements. AIAA J. 44 (11), 2504–2514.Google Scholar
Gregory, N. T. & Walker, W. S. 1956 The Effect on Transition of Isolated Surface Excrescences in the Boundary Layer. HM Stationery Office.Google Scholar
Honein, A. E. & Moin, P. 2004 Higher entropy conservation and numerical stability of compressible turbulence simulations. J. Comput. Phys. 201 (2), 531–545.Google Scholar
Iyer, P. S. & Mahesh, K. 2013 High-speed boundary-layer transition induced by a discrete roughness element. J. Fluid Mech. 729, 524–562.Google Scholar
Juliano, T. J., Schneider, S. P., Aradag, S. & Knight, D. 2008 Quiet-flow Ludwieg tube for hypersonic transition research. AIAA J. 46 (7), 1757–1763.CrossRefGoogle Scholar
Klebanoff, P. S., Cleveland, W. G. & Tidstrom, K. D. 1992 On the evolution of a turbulent boundary layer induced by a three-dimensional roughness element. J. Fluid Mech. 237, 101–187.Google Scholar
Mahesh, K. 2013 The interaction of jets with crossflow. Annu. Rev. Fluid Mech. 45, 379–407.CrossRefGoogle Scholar
Marxen, O., Iaccarino, G. & Shaqfeh, E. S. G. 2010 Disturbance evolution in a Mach 4.8 boundary layer with two-dimensional roughness-induced separation and shock. J. Fluid Mech. 648, 435–469.Google Scholar
Mavriplis, D. J.2003 Revisiting the least-squares procedure for gradient reconstruction on unstructured meshes. AIAA Paper 2003-3986.Google Scholar
Nompelis, I., Drayna, T. W. & Candler, G. V.2005 A parallel unstructured implicit solver for reacting flow simulation. AIAA Paper 2005-4867.Google Scholar
Pirozzoli, S. 2010 Generalized conservative approximations of split convective derivative operators. J. Comput. Phys. 229 (19), 7180–7190.Google Scholar
Pirozzoli, S. & Bernardini, M. 2011 Turbulence in supersonic boundary layers at moderate Reynolds number. J. Fluid Mech. 688, 120–168.Google Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.Google Scholar
Redford, J. A., Sandham, N. D. & Roberts, G. T. 2010 Compressibility effects on boundary-layer transition induced by an isolated roughness element. AIAA J. 48 (12), 2818–2830.Google Scholar
Reshotko, E. 2007 Is $Re_{\theta }/M_{e}$ a meaningful transition criterion? AIAA J. 45 (7), 1441–1443.Google Scholar
Reshotko, E. & Tumin, A. 2004 Role of transient growth in roughness-induced transition. AIAA J. 42 (4), 766–770.Google Scholar
Rowley, C. W., Mezic, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schneider, S. P. 2008a Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.Google Scholar
Schneider, S. P. 2008b Development of hypersonic quiet tunnels. J. Spacecr. Rockets 45 (4), 641–664.Google Scholar
Simpson, R. L. 2001 Junction flows. Annu. Rev. Fluid Mech. 33, 415–443.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to ${R}_{\theta }= 1410$ . J. Fluid Mech. 187, 61–98.Google Scholar
Subbareddy, P. & Candler, G. 2009 A fully discrete, kinetic energy consistent finite-volume scheme for compressible flows. J. Comput. Phys. 228, 1347–1364.Google Scholar
Tani, I., Komoda, H. & Komatsu, Y.1962. Boundary-layer transition by isolated roughness. Tech. Rep. 375. Aeronautical Research Institute, University of Tokyo.Google Scholar
Wheaton, B. M. & Schneider, S. P.2010 Roughness-induced instability in a laminar boundary layer at Mach 6. AIAA Paper 2010-1574.Google Scholar
Wheaton, B. M. & Schneider, S. P. 2012 Roughness-induced instability in a hypersonic laminar boundary layer. AIAA J. 50 (6), 1245–1256.Google Scholar
Wheaton, B. M. & Schneider, S. P. 2014 Hypersonic boundary-layer instabilities due to near-critical roughness. J. Spacecr. Rockets 51 (1), 327–342.Google Scholar
Whitehead, A. H.1969 Flow-field and drag characteristics of several boundary-layer tripping elements in hypersonic flow. NASA TN D-5454.Google Scholar
Wright, M. J., Candler, G. V. & Prampolini, M. 1996 Data parallel lower–upper relaxation method for the Navier–Stokes equations. AIAA J. 34, 1371–1377.CrossRefGoogle Scholar