Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-02T21:13:38.080Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a 30R long turbulent pipe flow at R+ = 685: large- and very large-scale motions

Published online by Cambridge University Press:  05 April 2012

Xiaohua Wu ,
J. R. Baltzer  and
R. J. Adrian
Xiaohua Wu
Affiliation:
Department of Mechanical Engineering, Royal Military College of Canada, Kingston, Ontario, K7K 7B4, Canada
J. R. Baltzer
Affiliation:
School for Engineering of Matter, Transport and Energy, Arizona State University, PO Box 876106, Tempe, AZ 85287-6106, USA
R. J. Adrian*
Affiliation:
School for Engineering of Matter, Transport and Energy, Arizona State University, PO Box 876106, Tempe, AZ 85287-6106, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fully developed incompressible turbulent pipe flow at Reynolds number 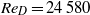(based on bulk velocity) and Kármán number 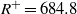is simulated in a periodic domain with a length of 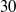pipe radii 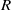. While single-point statistics match closely with experimental measurements, questions have been raised of whether streamwise energy spectra calculated from spatial data agree with the well-known bimodal spectrum shape in premultiplied spectra produced by experiments using Taylor’s hypothesis. The simulation supports the importance of large- and very large-scale motions (VLSMs, with streamwise wavelengths exceeding 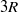). Wavenumber spectral analysis shows evidence of a weak peak or flat region associated with VLSMs, independent of Taylor’s hypothesis, and comparisons with experimental spectra are consistent with recent findings (del Álamo & Jiménez, J. Fluid Mech., vol. 640, 2009, pp. 5–26) that the long-wavelength streamwise velocity energy peak is overestimated when Taylor’s hypothesis is used. Yet, the spectrum behaviour retains otherwise similar properties to those documented based on experiment. The spectra also reveal the importance of motions of long streamwise length to the 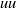energy and 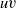Reynolds stress and support the general conclusions regarding these quantities formed using experimental measurements. Space–time correlations demonstrate that low-level correlations involving very large scales persist over 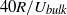in time and indicate that these motions convect at approximately the bulk velocity, including within the region approaching the wall. These very large streamwise motions are also observed to accelerate the flow near the wall based on force spectra, whereas smaller scales tend to decelerate the mean streamwise flow profile, in accordance with the behaviour observed in net force spectra of prior experiments. Net force spectra are resolved for the first time in the buffer layer and reveal an unexpectedly complex structure.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 698 , 10 May 2012 , pp. 235 - 281
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
2. Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
3. del Álamo, J. C. & Jiménez, J. 2001 Direct numerical simulation of the very large anisotropic scales in a turbulent channel. In Center for Turbulence Research Annual Research Briefs, pp. 329–341. Stanford University.Google Scholar
4. del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15, L41–L44.Google Scholar
5. del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
6. del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
7. Bailey, S. C. C., Hultmark, M., Smits, A. J. & Schultz, M. P. 2008 Azimuthal structure of turbulence in high Reynolds number pipe flow. J. Fluid Mech. 615, 121–138.CrossRefGoogle Scholar
8. Balakumar, B. J. & Adrian, R. J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
9. Bullock, K. J., Cooper, R. E. & Abernathy, F. H. 1978 Structural similarity in radial correlations and spectra of longitudinal velocity fluctuations in pipe flow. J. Fluid Mech. 88, 585–608.CrossRefGoogle Scholar
10. Chin, C. C., Hutchins, N., Ooi, A. S. H. & Marusic, I. 2009 Use of direct numerical simulation (DNS) data to investigate spatial resolution issues in measurements of wall-bounded turbulence. Meas. Sci. Technol. 20 (11), 115401.Google Scholar
11. Chin, C., Ooi, A. S. H., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22, 115107.Google Scholar
12. Choi, H. & Moin, P. 1990 On the space-time characteristics of wall-pressure fluctuations. Phys. Fluids A 2, 1450–1460.Google Scholar
13. Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
14. Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.CrossRefGoogle Scholar
15. Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–210.CrossRefGoogle Scholar
16. Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
17. Hites, M. 1997 Scaling of high-Reynolds number turbulent boundary layers in the national diagnostic facility. PhD thesis, Illinois Institute of Technology, Chicago, IL.Google Scholar
18. Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
19. Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2010 Scaling of near-wall turbulence in pipe flow. J. Fluid Mech. 649, 103–113.CrossRefGoogle Scholar
20. Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
21. Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
22. Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.CrossRefGoogle Scholar
23. Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
24. Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.CrossRefGoogle Scholar
25. Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids A 5, 695–706.CrossRefGoogle Scholar
26. Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
27. Krogstad, P. A., Kaspersen, J. H. & Rimestad, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10, 949–957.Google Scholar
28. Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
29. LeHew, J., Guala, M. & McKeon, B. J. 2011 A study of the three-dimensional spectral energy distribution in a zero pressure gradient turbulent boundary layer. Exp. Fluids 51, 997–1012.Google Scholar
30. Lekakis, I. C. 1988 Coherent structures in fully developed turbulent pipe flow. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
31. Liu, Z.-C., Adrian, R. J. & Hanratty, T. J. 2001 Large-scale modes of turbulent channel flow: transport and structure. J. Fluid Mech. 448, 53–80.Google Scholar
32. Marusic, I. & Adrian, R. J. 2012 Scaling issues and the role of organized motion in wall turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R. ). Cambridge University Press.Google Scholar
33. Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
34. Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
35. Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21, 111703.Google Scholar
36. McConachie, P. J. 1981 The distribution of convection velocities in turbulent pipe flow. J. Fluid Mech. 103, 65–85.Google Scholar
37. McKeon, B. J. & Morrison, J. F. 2007 Asymptotic scaling in turbulent pipe flow. Phil. Trans. R. Soc. Lond. A 365, 771–787.Google ScholarPubMed
38. Moin, P. 2009 Revisiting Taylor’s hypothesis. J. Fluid Mech. 640, 1–4.Google Scholar
39. Monty, J. P. & Chong, M. S. 2009 Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. J. Fluid Mech. 633, 461–474.Google Scholar
40. Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
41. Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
42. Ng, H. C. H., Monty, J. P., Hutchins, N., Chong, M. S. & Marusic, I. 2011 Comparison of turbulent channel and pipe flows with varying Reynolds number. Exp. Fluids 51, 1261–1281.CrossRefGoogle Scholar
43. Perry, A. E. & Abell, C. J. 1975 Scaling laws for pipe-flow turbulence. J. Fluid Mech. 67, 257–271.Google Scholar
44. Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
45. Sreenivasan, K. R. 1987 A unified view of the origin and morphology of the turbulent boundary layer structure. In Turbulence Management and Relaminarization (ed. Liepmann, H. W. & Narasimha), R. ). pp. 37–61. Springer.Google Scholar
46. Sreenivasan, K. R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region, and the mean velocity in turbulent pipe and channel flows. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R. ). pp. 253–272. Computational Mechanics Publications.Google Scholar
47. Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. 164 (919), 476–490.Google Scholar
48. Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
49. den Toonder, J. M. J. & Nieuwstadt, F. T. M. 1997 Reynolds number effects in a turbulent pipe flow for low to moderate Re. Phys. Fluids 9, 3398–3409.CrossRefGoogle Scholar
50. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
51. Vallikivi, M., Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2011 Turbulence measurements in pipe flow using a nano-scale thermal anemometry probe. Exp. Fluids 51, 1521–1527.CrossRefGoogle Scholar
52. Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.Google Scholar
53. Zhao, X. & He, G.-W. 2009 Space-time correlations of fluctuating velocities in turbulent shear flows. Phys. Rev. E 79, 046316.CrossRefGoogle ScholarPubMed
54. Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar