Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T22:14:57.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusion transients in convection rolls

Published online by Cambridge University Press:  05 February 2021

Qingqing Yin ,
Yunyun Li ,
Baowen Li ,
Fabio Marchesoni ,
Shubhadip Nayak  and
Pulak K. Ghosh Open the ORCID record for Pulak K. Ghosh [Opens in a new window]
Qingqing Yin
Affiliation:
Center for Phononics and Thermal Energy Science, Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology, School of Physics Science and Engineering, Tongji University, Shanghai200092, PR China
Yunyun Li*
Affiliation:
Center for Phononics and Thermal Energy Science, Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology, School of Physics Science and Engineering, Tongji University, Shanghai200092, PR China
Baowen Li
Affiliation:
Paul M. Rady Department of Mechanical Engineering and Department of Physics, University of Colorado, Boulder, Colorado 80309-0427, USA
Fabio Marchesoni
Affiliation:
Center for Phononics and Thermal Energy Science, Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology, School of Physics Science and Engineering, Tongji University, Shanghai200092, PR China Dipartimento di Fisica, Università di Camerino, I-62032Camerino, Italy
Shubhadip Nayak
Affiliation:
Department of Chemistry, Presidency University, Kolkata700073, India
Pulak K. Ghosh*
Affiliation:
Department of Chemistry, Presidency University, Kolkata700073, India
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

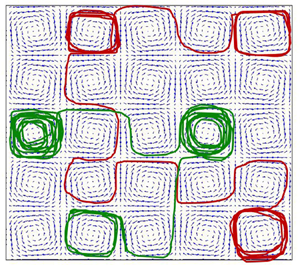
We numerically investigated the phenomenon of non-Gaussian normal diffusion of a Brownian colloidal particle in a periodic array of planar counter-rotating convection rolls. At high Péclet numbers, normal diffusion is observed to occur at all times with non-Gaussian transient statistics. This effect vanishes with increasing the observation time. The displacement distributions decay either slower or faster than a Gaussian function, depending on the flow parameters. The sign of their excess kurtosis is related to the difference between two dynamical time scales, namely, the mean exit time of the particle out of a convection roll and its circulation period inside it.

JFM classification

Complex Fluids: Colloids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A14
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bhattacharya, S., Sharma, D.K., Saurabh, S., De, S., Sain, A., Nandi, A. & Chowdhury, A. 2013 Plasticization of poly(vinylpyrrolidone) thin films under ambient humidity: insight from single-molecule tracer diffusion dynamics. J. Phys. Chem. B 117, 7771–7782.CrossRefGoogle ScholarPubMed
Chandrasekhar, S. 1967 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chaudhuri, P., Berthier, P. & Kob, W. 2007 Universal nature of particle displacements close to glass and jamming transitions. Phys. Rev. Lett. 99, 060604.CrossRefGoogle ScholarPubMed
Childress, S. 1979 Alpha-effect in flux ropes and sheets. Phys. Earth Planet. Inter. 20, 172–180.CrossRefGoogle Scholar
Chubynsky, M.V. & Slater, G.W. 2014 Diffusing diffusivity: a model for anomalous, yet Brownian, diffusion. Phys. Rev. Lett. 113, 098302.CrossRefGoogle Scholar
Cromer, N.O. 1995 Many oscillations of a rigid rod. Am. J. Phys. 63, 112–121.CrossRefGoogle Scholar
Eaves, J.D. & Reichman, D.R. 2009 Spatial dimension and the dynamics of supercooled liquids. Proc. Natl Acad. Sci. USA 106, 15171–15175.CrossRefGoogle ScholarPubMed
Gardiner, C. 2009 Stochastic Methods: A Handbook for the Natural and Social Sciences. Springer.Google Scholar
Ghosh, S.K., Cherstvy, A.G., Grebenkov, D.S. & Metzler, R. 2016 Anomalous, non-Gaussian tracer diffusion in crowded two-dimensional environments. New J. Phys. 18, 013027.CrossRefGoogle Scholar
Gradshteyn, I.S. & Ryzhik, I.M. 2007 Table of Integrals, Series, and Products, 7th edn. Academic Press.Google Scholar
Guan, J., Wang, B. & Granick, S. 2014 Even hard-sphere colloidal suspensions display Fickian yet non-Gaussian diffusion. ACS Nano 8, 3331–3336.CrossRefGoogle ScholarPubMed
He, W., Song, H., Su, Y., Geng, L., Ackerson, B.J., Peng, H.B. & Tong, P. 2016 Dynamic heterogeneity and non-Gaussian statistics for acetylcholine receptors on live cell membrane. Nat. Commun. 7, 11701.CrossRefGoogle ScholarPubMed
Kegel, W.K. & van Blaaderen, A. 2000 Direct observation of dynamical heterogeneities in colloidal hard-sphere suspensions. Science 287, 290–293.CrossRefGoogle ScholarPubMed
Kendall, M.G. & Stuart, A. 1976 The Advanced Theory of Statistics, 3rd edn, vol. 1. Griffin.Google Scholar
Kim, J., Kim, C. & Sung, B.J. 2013 Simulation study of seemingly Fickian but heterogeneous dynamics of two dimensional colloids. Phys. Rev. Lett. 110, 047801.CrossRefGoogle ScholarPubMed
Kirby, B.J. 2010 Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. Cambridge University Press.CrossRefGoogle Scholar
Kloeden, P.E. & Platen, E. 1992 Numerical Solution of Stochastic Differential Equations. Springer.CrossRefGoogle Scholar
Kwon, G., Sung, B.J. & Yethiraj, A. 2014 Dynamics in crowded environments: is non-Gaussian Brownian diffusion normal? J. Phys. Chem. B 118, 8128–8134.CrossRefGoogle ScholarPubMed
Leptos, K.C., Guasto, J.S., Gollub, J.P., Pesci, A.I. & Goldstein, R.E. 2009 Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett. 103, 198103.CrossRefGoogle ScholarPubMed
Li, Y., Li, L., Marchesoni, F., Debnath, D. & Ghosh, P.K. 2020 Active diffusion in convection rolls. Phys. Rev. Res. 2, 013250.CrossRefGoogle Scholar
Li, Y., Marchesoni, F., Debnath, D. & Ghosh, P.K. 2019 Non-Gaussian normal diffusion in a fluctuating corrugated channel. Phys. Rev. Res. 1, 033003.CrossRefGoogle Scholar
Manikantan, H. & Saintillan, D. 2013 Subdiffusive transport of fluctuating elastic filaments in cellular flows. Phys. Fluids 25, 073603.CrossRefGoogle Scholar
Moffatt, H.K., Zaslavsky, G.M., Comte, P. & Tabor, M. (Eds.) 1992 Topological Aspects of the Dynamics of Fluids and Plasmas. Springer.CrossRefGoogle Scholar
Rosenbluth, M.N., Berk, H.L., Doxas, I. & Horton, W. 1987 Effective diffusion in laminar convective flows. Phys. Fluids 30, 2636–2647.CrossRefGoogle Scholar
Sarracino, A., Cecconi, F., Puglisi, A. & Vulpiani, A. 2016 Nonlinear response of inertial tracers in steady laminar flows: differential and absolute negative mobility. Phys. Rev. Lett. 117, 174501.CrossRefGoogle ScholarPubMed
Shraiman, B.I. 1987 Diffusive transport in a Rayleigh-Bénard convection cell. Phys. Rev. A 36, 261–267.CrossRefGoogle Scholar
Solomon, T.H. & Gollub, J.P. 1988 Chaotic particle transport in time-dependent Rayleigh-Bénard convection. Phys. Rev. A 38, 6280–6286.CrossRefGoogle ScholarPubMed
Solomon, T.H. & Mezić, I. 2003 Uniform resonant chaotic mixing in fluid flows. Nature 425, 376–380.CrossRefGoogle ScholarPubMed
Soward, A.M. 1987 Fast dynamo action in a steady flow. J. Fluid Mech. 180, 267–295.CrossRefGoogle Scholar
Tabeling, P. 2002 Two-dimensional turbulence: a physicist approach. Phys. Rep. 362, 1–62.CrossRefGoogle Scholar
Torney, C. & Neufeld, Z. 2007 Transport and aggregation of self-propelled particles in fluid flows. Phys. Rev. Lett. 99, 078101.CrossRefGoogle ScholarPubMed
Wang, B., Anthony, S.M., Bae, S.C. & Granick, S. 2009 Anomalous yet Brownian. Proc. Natl Acad. Sci. USA 106, 15160–15164.CrossRefGoogle ScholarPubMed
Wang, B., Kuo, J., Bae, C. & Granick, S. 2012 When Brownian diffusion is not Gaussian. Nat. Mater. 11, 481–485.CrossRefGoogle Scholar
Weeks, E.R., Crocker, J.C., Levitt, A.C., Schofield, A. & Weitz, D.A. 2000 Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science 287, 627–631.CrossRefGoogle ScholarPubMed
Weiss, N.O. 1966 The expulsion of magnetic flux by eddies. Proc. R. Soc. Lond. A293, 310–328.Google Scholar
Yin, Q., Li, Y., Marchesoni, F., Debnath, D. & Ghosh, P.K. 2021 Excess diffusion of a driven colloidal particle in a convection array. Chin. Phys. Lett. (to be published).Google Scholar
Young, W., Pumir, A. & Pomeau, Y. 1989 Anomalous diffusion of tracer in convection rolls. Phys. Fluids A 1, 462–469.CrossRefGoogle Scholar
Young, Y.-N. & Shelley, M.J. 2007 Stretch-coil transition and transport of fibers in cellular flows. Phys. Rev. Lett. 99, 058303.CrossRefGoogle ScholarPubMed
Zheng, X., ten Hagen, B., Kaiser, A., Wu, M., Cui, H., Silber-Li, Z. & Löwen, H. 2013 Non-Gaussian statistics for the motion of self-propelled Janus particles: experiment versus theory. Phys. Rev. E 88, 032304.CrossRefGoogle ScholarPubMed