Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kostaschuk, Ray
Nasr‐Azadani, Mohamad M.
Meiburg, Eckart
Wei, Taoyuan
Chen, Zhongyuan
Negretti, Maria Eletta
Best, Jim
Peakall, Jeff
and
Parsons, Daniel R.
2018.
On the Causes of Pulsing in Continuous Turbidity Currents.
Journal of Geophysical Research: Earth Surface,
Vol. 123,
Issue. 11,
p.
2827.
Neamtu-Halic, Marius M.
Krug, Dominik
Haller, George
and
Holzner, Markus
2019.
Lagrangian coherent structures and entrainment near the turbulent/non-turbulent interface of a gravity current.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
824.
Dorrell, R. M.
Peakall, J.
Darby, S. E.
Parsons, D. R.
Johnson, J.
Sumner, E. J.
Wynn, R. B.
Özsoy, E.
and
Tezcan, D.
2019.
Self-sharpening induces jet-like structure in seafloor gravity currents.
Nature Communications,
Vol. 10,
Issue. 1,
Martin, Antoine
Negretti, M. Eletta
and
Hopfinger, E. J.
2019.
Development of gravity currents on slopes under different interfacial instability conditions.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
180.
Zemach, T.
Ungarish, M.
Martin, A.
and
Negretti, M. E.
2019.
On gravity currents of fixed volume that encounter a down-slope or up-slope bottom.
Physics of Fluids,
Vol. 31,
Issue. 9,
Tanimoto, Yukinobu
Ouellette, Nicholas T.
and
Koseff, Jeffrey R.
2020.
Interaction between an inclined gravity current and a pycnocline in a two-layer stratification.
Journal of Fluid Mechanics,
Vol. 887,
Issue. ,
Thomson, Richard E.
Kulikov, Evgueni A.
Spear, David J.
Johannessen, Sophia C.
and
Peter Wills, W.
2020.
A Role for Gravity Currents in Cross‐Sill Estuarine Exchange and Subsurface Inflow to the Southern Strait of Georgia.
Journal of Geophysical Research: Oceans,
Vol. 125,
Issue. 4,
Dai, Albert
and
Huang, Yu-Lin
2020.
Experiments on gravity currents propagating on unbounded uniform slopes.
Environmental Fluid Mechanics,
Vol. 20,
Issue. 6,
p.
1637.
Martin, A.
Negretti, M. E.
Ungarish, M.
and
Zemach, T.
2020.
Propagation of a continuously supplied gravity current head down bottom slopes.
Physical Review Fluids,
Vol. 5,
Issue. 5,
Jarrín Oseguera, Pablo Isaac
and
Calle Chumo, Rafael Norberto
2021.
Influencia de las condiciones iniciales sobre los parámetros de velocidad y aceleración de las corrientes por gravedad.
Revista Científica y Tecnológica UPSE,
Vol. 8,
Issue. 2,
p.
01.
Negretti, M. Eletta
Tucciarone, Francesco L.
and
Wirth, Achim
2021.
Intruding gravity currents and re-circulation in a rotating frame: Laboratory experiments.
Physics of Fluids,
Vol. 33,
Issue. 9,
De Falco, M.C.
Adduce, C.
Negretti, M.E.
and
Hopfinger, E.J.
2021.
On the dynamics of quasi-steady gravity currents flowing up a slope.
Advances in Water Resources,
Vol. 147,
Issue. ,
p.
103791.
Dai, Albert
and
Huang, Yu-Lin
2021.
Boussinesq and non-Boussinesq gravity currents propagating on unbounded uniform slopes in the deceleration phase.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Wells, Mathew G.
and
Dorrell, Robert M.
2021.
Turbulence Processes Within Turbidity Currents.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
59.
De Falco, M.C.
Adduce, C.
and
Maggi, M.R.
2021.
Gravity currents interacting with a bottom triangular obstacle and implications on entrainment.
Advances in Water Resources,
Vol. 154,
Issue. ,
p.
103967.
Maggi, Maria Rita
Adduce, Claudia
and
Negretti, Maria Eletta
2022.
Lock-release gravity currents propagating over roughness elements.
Environmental Fluid Mechanics,
Vol. 22,
Issue. 2-3,
p.
383.
Negretti, M.E.
Martin, A.
and
Naaim-Bouvet, F.
2022.
Simultaneous velocity–density measurements of downslope density clouds.
Advances in Water Resources,
Vol. 164,
Issue. ,
p.
104215.
Wu, Ching-Sen
and
Dai, Albert
2023.
Gravity currents from a constant inflow on unbounded uniform slopes.
Journal of Hydraulic Research,
Vol. 61,
Issue. 6,
p.
880.
Peacock, Thomas
and
Ouillon, Raphael
2023.
The Fluid Mechanics of Deep-Sea Mining.
Annual Review of Fluid Mechanics,
Vol. 55,
Issue. 1,
p.
403.
Ungarish, M.
2023.
Strongly supercritical non-Boussinesq sustained gravity currents: Time-dependent and steady-state approximate solutions.
Physical Review Fluids,
Vol. 8,
Issue. 5,
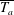 $\overline{T_{a}}$, expressing the rate of velocity increase, the currents can adjust gradually to the slope conditions (small
$\overline{T_{a}}$, expressing the rate of velocity increase, the currents can adjust gradually to the slope conditions (small 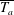 $\overline{T_{a}}$) or go through acceleration–deceleration cycles (large
$\overline{T_{a}}$) or go through acceleration–deceleration cycles (large 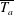 $\overline{T_{a}}$). In the latter case, the KH billows at the interface have a strong effect on the flow dynamics, and are observed to cause boundary layer separation. Comparison of currents on concave and straight slopes reveals that the downhill deceleration on concave slopes has no qualitative influence, i.e. the dynamics is entirely dominated by the initial acceleration and ensuing KH billows. Following the similarity theory of Turner 1973 (Buoyancy Effects in Fluids. Cambridge University Press), we derive a general equation for the depth-integrated velocity that exhibits all driving and retarding forces. Comparison of this equation with the experimental velocity data shows that when
$\overline{T_{a}}$). In the latter case, the KH billows at the interface have a strong effect on the flow dynamics, and are observed to cause boundary layer separation. Comparison of currents on concave and straight slopes reveals that the downhill deceleration on concave slopes has no qualitative influence, i.e. the dynamics is entirely dominated by the initial acceleration and ensuing KH billows. Following the similarity theory of Turner 1973 (Buoyancy Effects in Fluids. Cambridge University Press), we derive a general equation for the depth-integrated velocity that exhibits all driving and retarding forces. Comparison of this equation with the experimental velocity data shows that when 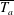 $\overline{T_{a}}$ is large, bottom friction and entrainment are large in the region of appearance of KH billows. The large bottom friction is confirmed by the measured high Reynolds stresses in these regions. The head velocity does not exhibit the same behaviour as the layer velocity. It gradually approaches an equilibrium state even when the acceleration parameter of the layer is large.
$\overline{T_{a}}$ is large, bottom friction and entrainment are large in the region of appearance of KH billows. The large bottom friction is confirmed by the measured high Reynolds stresses in these regions. The head velocity does not exhibit the same behaviour as the layer velocity. It gradually approaches an equilibrium state even when the acceleration parameter of the layer is large.

