Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T16:39:33.274Z Has data issue: false hasContentIssue false
  • English
  • Français

The detrimental effect of hydrodynamic interactions on the process of Brownian flocculation in shear flow

Published online by Cambridge University Press:  29 April 2014

Krzysztof A. Mizerski
Krzysztof A. Mizerski*
Affiliation:
Department of Magnetism, Institute of Geophysics, Polish Academy of Sciences, ul. Ksiecia Janusza 64, 01-452 Warsaw, Poland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The problem of Brownian flocculation of spherical particles in strong shearing flow without hydrodynamic interactions is studied in detail using the singular perturbation method. All other types of interparticle interactions, such as van der Waals or Lennard-Jones forces, are also ignored. In the limit of strong external flow, the strength of which is measured by the Péclet number (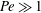$Pe\gg 1$), a complicated boundary layer structure for the pair probability density function (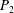$P_{2}$) is identified and the complete stationary spatial distribution of 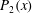$P_{2}(\boldsymbol {x})$ in the domain is found. The results, in particular the total mass flux in the accumulation process, are compared qualitatively and quantitatively with the case where the spheres interact hydrodynamically and it is demonstrated that the hydrodynamic interactions tend to decrease the rate of flocculation. An explicit simple formula for the flocculation rate for a general form of hydrodynamic interactions is provided. The limit of small Péclet number is also discussed to confirm the conclusion on the detrimental influence of hydrodynamic interactions on the rate of Brownian flocculation in shearing flow.

JFM classification

Mathematical Foundations: General fluid mechanics Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 328 - 349
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications.Google Scholar
Acrivos, A. & Taylor, T. D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 5, 387–394.CrossRefGoogle Scholar
Batchelor, G. K. 1979 Mass transfer from a particle suspended in fluid with a steady linear ambient velocity distribution. J. Fluid Mech. 95, 369–400.CrossRefGoogle Scholar
Batchelor, G. K. & Green, J. T. 1972 The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56, 375–400.Google Scholar
Dormy, E., Jault, E. & Soward, A. M. 2002 A super-rotating shear layer in magnetohydrodynamic spherical Couette flow. J. Fluid Mech. 452, 263–291.CrossRefGoogle Scholar
Elrick, D. E. 1962 Source functions for diffusion in uniform shear flow. Austral. J. Phys. 15, 283–288.Google Scholar
Frankel, N. A. & Acrivos, A. 1968 Heat and mass transfer from small spheres and cylinders freely suspended in shear flow. Phys. Fluids 11, 1913–1918.Google Scholar
Kim, S. & Karrila, S. J. 2005 Microhydrodynamics. Principles and Selected Applications. Dover Publications.Google Scholar
Levich, V. G. 1962 Physiochemical Hydrodynamics. Prentice-Hall.Google Scholar
von Mises, R. 1927 Bemerkungen zur Hydrodynamik. Z. Angew. Math. Mech. 7, 425–431.Google Scholar
Noh, D. S., Koh, Y. & Kang, I. S. 1998 Numerical solutions for shape evolution of a particle growing in axisymmetric flows of supersaturated solution. J. Cryst. Growth 183, 427–440.Google Scholar
Roberts, P. H. 1967 Singularities of Hartmann layers. Proc. R. Soc. Lond. A 300, 94–107.Google Scholar
Rotne, J. & Prager, S. 1969 Variational treatment of hydrodynamic interaction in polymers. J. Chem. Phys. 50, 4831–4837.Google Scholar
Russel, W. B., Saville, D. A. & Showalter, W. A. 1989 Colloidal Dispersions. Cambridge University Press.Google Scholar
Smoluchowski, M. 1917 Versuch einer mathematischen Theorie der Koagulationkinetik kolloider lösungen. Z. Phys. Chem. 92, 129–168.Google Scholar
Wang, H., Zinchenko, A. Z. & Davis, R. H. 1994 The collision rate of small drops in linear flow fields. J. Fluid Mech. 265, 161–188.Google Scholar
Yamakawa, H. 1970 Transport properties of polymer chains in dilute solution: hydrodynamic interaction. J. Chem. Phys. 53, 436–443.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 1995 Collision rates of spherical drops or particles in a shear flow at arbitrary Péclet numbers. Phys. Fluids 7, 2310–2327.CrossRefGoogle Scholar