Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T15:24:31.613Z Has data issue: false hasContentIssue false
  • English
  • Français

Depth and minimal slope for surface flows of cohesive granular materials on inclined channels

Published online by Cambridge University Press:  19 June 2013

Alain de Ryck  and
Olivier Louisnard
Alain de Ryck
Affiliation:
Centre RAPSODEE, UMR CNRS 5302, Université de Toulouse, Ecole des Mines d’Albi, 81013 Albi CEDEX 09, France
Olivier Louisnard*
Affiliation:
Centre RAPSODEE, UMR CNRS 5302, Université de Toulouse, Ecole des Mines d’Albi, 81013 Albi CEDEX 09, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present analytical predictions of the depth and onset slope of the steady surface flow of a cohesive granular material in an inclined channel. The rheology of Jop, Forterre & Pouliquen (Nature, vol. 441, 2006, pp. 727–730) is used, assuming co-axiality between the stress and strain-rate tensors, and a coefficient of friction dependent on the strain rate through the dimensionless inertial number 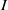$I$. This rheological law is augmented by a constant stress representing cohesion. Our analysis does not rely on a precise 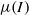$\mu (I)$ functional, but only on its asymptotic power law in the limit of vanishing strain rates. Assuming a unidirectional flow, the Navier–Stokes equations can be solved explicitly to yield parametric equations of the iso-velocity lines in the plane perpendicular to the flow. Two types of channel walls are considered: rough and smooth, depicting walls whose friction coefficient is respectively larger or smaller than that of the flowing material. The steady flow starts above a critical onset angle and consists of a sheared zone confined between a surface plug flow and a deep dead zone. The details of the flow are discussed, depending on dimensionless parameters relating the static friction coefficient, cohesion strength of the material, incline angle, wall friction, and channel width. The depths of the flow at the centre of the channel and at the walls are calculated by a force balance on the flowing material. The critical angle for the onset of the flow is also calculated, and is found to be strongly dependent on the channel width, in agreement with experimental results on heap stability and in rotating drums. Our results predict the important conclusion that a cohesive material always starts to flow for an incline angle lower than 90° between smooth walls, whereas in a narrow enough channel with rough walls, it may not flow, even if the channel is inclined vertically.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , pp. 191 - 235
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brewster, R., Crest, G. S., Landry, J. W. & Levine, A. J. 2005 Plug flow and the breakdown of Bagnold scaling in cohesive granular flows. Phys. Rev. E 72, 061301.CrossRefGoogle ScholarPubMed
Cassar, C., Nicolas, M. & Pouliquen, O. 2005 Submarine granular flows down inclined planes. Phys. Fluids 17 (10), 103301.Google Scholar
Chevoir, F., Roux, J. N., da Cruz, F., Rognon, P. G. & Koval, G. 2009 Friction law in dense granular flows. Powder Technol. 190 (1–2), 264–268.CrossRefGoogle Scholar
da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulations of plane shear. Phys. Rev. E 72, 021309.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.Google Scholar
GDR MiDi, 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Hatano, T. 2007 Power-law friction in closely packed granular materials. Phys. Rev. E 75, 060301.CrossRefGoogle ScholarPubMed
Hungr, O. 1995 A model for the runout analysis of rapid flow slides, debris flows, and avalanches. Can. Geotech. J. 32 (4), 610–623.Google Scholar
Jenike, A. W. 1987 A theory of flow of particulate solids in converging and diverging channels based on a conical yield function. Powder Technol. 50, 229–236.Google Scholar
Jop, P. 2008 Hydrodynamic modeling of granular flows in a modified Couette cell. Phys. Rev. E 77, 032301.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in dense granular flows. J. Fluid Mech. 541, 167–192.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441, 727–730.Google Scholar
Kamrin, K. & Bazant, M. Z. 2007 Stochastic flow rule for granular materials. Phys. Rev. E 75, 041301.Google Scholar
Kamrin, K. & Koval, G. 2012 Non-local constitutive relation for steady granular flow. Phys. Rev. Lett. 108, 178301.Google Scholar
Kern, M. A., Tiefenbacher, F. & McElwaine, J. N. 2004 The rheology of snow in large chute flows. Cold Reg. Sci. Technol. 39, 181–192.Google Scholar
Komatsu, T. S., Inagaki, S., Nakagawa, N. & Nasuno, S. 2001 Creep motion in a granular pile exhibiting steady surface flow. Phys. Rev. Lett. 86, 1757–1760.CrossRefGoogle Scholar
Koval, G., Chevoir, F., Roux, J. N., Sulem, J. & Corfdir, A. 2011 Interface roughness effect on slow cyclic annular shear of granular materials. Granul. Matt. 13, 525–540.Google Scholar
Koval, G., Roux, J. N., Corfdir, A. & Chevoir, F. 2009 Annular shear of cohesionless granular materials: from the inertial to quasistatic regime. Phys. Rev. E 79, 021306.Google Scholar
Métayer, J. F., Richard, P., Faisant, A. & Delannay, R. 2010 Electrically induced tunable cohesion in granular systems. J. Stat. Mech. 2010 (08), P08003.Google Scholar
Nedderman, R. M. 1992 Statics and Kinematics of Granular Materials. Cambridge University Press.Google Scholar
Nowak, S., Samadani, A. & Kudrolli, A. 2005 Maximum angle of stability of a wet granular pile. Nat. Phys. 1, 50–52.Google Scholar
Peyneau, P.-E. & Roux, J.-N. 2008 Frictionless bead packs have macroscopic friction, but no dilatancy. Phys. Rev. E 78, 011307.Google Scholar
Pouliquen, O. & Renaut, N. 1996 Onset of granular flows on an inclined rough surface: dilatancy effects. J. Phys. II Paris 6, 923–935.Google Scholar
Renouf, M., Bonamy, D., Dubois, F. & Alart, P. 2005 Numerical simulation of two-dimensional steady granular flows in rotating drum: on surface flow rheology. Phys. Fluids 17, 103303.Google Scholar
Rognon, P. G., Roux, J. N., Naaïm, M. & Chevoir, F. 2008 Dense flows of cohesive granular materials. J. Fluid Mech. 596, 21–47.Google Scholar
de Ryck, A. 2008 Granular flows down inclined channels with a strain-rate dependent friction coefficient. Part II: cohesive materials. Granul. Matt. 10, 361–367.Google Scholar
de Ryck, A., Ansart, R. & Dodds, J. A. 2008 Granular flows down inclined channels with a strain-rate dependent friction coefficient. Part I: non-cohesive materials. Granul. Matt. 10, 353–360.CrossRefGoogle Scholar
de Ryck, A., Zhu, H. P., Wu, S. M., Yu, A. B. & Zulli, P. 2010 Numerical and theoretical investigation of the surface flows of granular materials on heaps. Powder Technol. 203, 125–132.CrossRefGoogle Scholar
Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.Google Scholar
Schaeffer, D. G. 1987 Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 66, 19–50.Google Scholar
Staron, L., Lagrée, P. Y., Josserand, C. & Lhuillier, D. 2010 Flow and jamming of a two-dimensional granular bed: toward a non-local rheology? Phys. Fluids 22 (11), 113303.CrossRefGoogle Scholar
Taberlet, N., Richard, P., Valance, A. & Losert, W. 2003 Superstable granular heap in a thin channel. Phys. Rev. Lett. 91 (26), 264301.Google Scholar
Weir, G. J. 1999 The intrinsic cohesion of granular materials. Powder Technol. 104 (1), 29–36.Google Scholar