Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T18:46:46.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Dense granular flow rheology in turbulent bedload transport

Published online by Cambridge University Press:  09 September 2016

Raphael Maurin ,
Julien Chauchat  and
Philippe Frey
Raphael Maurin
Affiliation:
Univ. Grenoble Alpes, Irstea, UR ETGR, 2 rue de la Papeterie-BP 76, F-38402 St-Martin-d’Hères, France
Julien Chauchat*
Affiliation:
Univ. Grenoble Alpes, LEGI, G-INP, CNRS, F-38000 Grenoble, France
Philippe Frey
Affiliation:
Univ. Grenoble Alpes, Irstea, UR ETGR, 2 rue de la Papeterie-BP 76, F-38402 St-Martin-d’Hères, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The local granular rheology is investigated numerically in turbulent bedload transport. Considering spherical particles, steady uniform configurations are simulated using a coupled fluid–discrete-element model. The stress tensor is computed as a function of the depth for a series of simulations varying the Shields number, the specific density and the particle diameter. 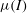The results are analysed in the framework of the $\unicode[STIX]{x1D707}(I)$ rheology and exhibit a collapse of both the shear to normal stress ratio and the solid volume fraction over a wide range of inertial numbers. Contrary to expectations, the effect of the interstitial fluid on the granular rheology is shown to be negligible, supporting recent work suggesting the absence of a clear transition between the free-fall and turbulent regimes. In addition, data collapse is observed up to unexpectedly high inertial numbers 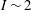$I\sim 2$, challenging the existing conceptions and parametrisation of the 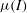$\unicode[STIX]{x1D707}(I)$ rheology. Focusing upon bedload transport modelling, the results are pragmatically analysed in the 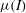$\unicode[STIX]{x1D707}(I)$ framework in order to propose a granular rheology for bedload transport. The proposed rheology is tested using a 1D volume-averaged two-phase continuous model, and is shown to accurately reproduce the dense granular flow profiles and the sediment transport rate over a wide range of Shields numbers. The present contribution represents a step in the upscaling process from particle-scale simulations towards large-scale applications involving complex flow geometry.

JFM classification

Granular media: Granular media Non-Newtonian Flows: Rheology Geophysical and Geological Flows: Sediment transport
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 490 - 512
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, 31400 Toulouse, France.

References

Amoudry, L. O. 2014 Extension of turbulence closure to two-phase sediment transport modelling: application to oscillatory sheet flows. Adv. Water Resour. 72, 110–121.CrossRefGoogle Scholar
Anderson, T. B. & Jackson, R. 1967 Fluid mechanical description of fluidized beds. Equations of motion. Ind. Engng Chem. Fundam. 6 (4), 527–539.CrossRefGoogle Scholar
Andreotti, B., Forterre, Y. & Pouliquen, O. 2013 Granular Media: Between Fluid and Solid. Cambridge University Press.CrossRefGoogle Scholar
Armanini, A., Capart, H., Fraccarollo, L. & Larcher, M. 2005 Rheological stratification in experimental free-surface flows of granular–liquid mixtures. J. Fluid Mech. 532, 269–319.CrossRefGoogle Scholar
Armanini, A., Larcher, M., Nucci, E. & Dumbser, M. 2014 Submerged granular channel flows driven by gravity. Adv. Water Resour. 63, 1–10.CrossRefGoogle Scholar
Aussillous, P., Chauchat, J., Pailha, M., Médale, M. & Guazzelli, E. 2013 Investigation of the mobile granular layer in bedload transport by laminar shearing flows. J. Fluid Mech. 736, 594–615.CrossRefGoogle Scholar
Bagnold, R. A. 1956 The flow of cohesionless grains in fluids. Phil. Trans. R. Soc. Lond. A 249, 235–297.Google Scholar
Berzi, D. & Jenkins, J. T. 2008 A theoretical analysis of free-surface flows of saturated granular–liquid mixtures. J. Fluid Mech. 608, 393–410.CrossRefGoogle Scholar
Berzi, D., di Prisco, C. G. & Vescovi, D. 2011 Constitutive relations for steady, dense granular flows. Phys. Rev. E 84, 031301.CrossRefGoogle ScholarPubMed
Börzsönyi, T., Ecke, R. E. & Mcelwaine, J. N. 2009 Patterns in flowing sand: understanding the physics of granular flow. Phys. Rev. Lett. 103, 178302.CrossRefGoogle ScholarPubMed
Bouzid, M., Trulsson, M., Claudin, P., Clément, E. & Andreotti, B. 2013 Nonlocal rheology of granular flows across yield conditions. Phys. Rev. Lett. 111, 238301.CrossRefGoogle ScholarPubMed
Boyer, F., Guazzelli, É. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.CrossRefGoogle ScholarPubMed
Campbell, C. S. 1990 Rapid granular flows. Annu. Rev. Fluid Mech. 22 (1), 57–90.CrossRefGoogle Scholar
Capart, H. & Fraccarollo, L. 2011 Transport layer structure in intense bed-load. Geophys. Res. Lett. 38 (20), L20402.CrossRefGoogle Scholar
Cassar, C., Nicolas, M. & Pouliquen, O. 2005 Submarine granular flows down inclined planes. Phys. Fluids 17 (10), 103301.CrossRefGoogle Scholar
Chauchat, J., Guillou, S., Pham Van Bang, D. & Dan Nguyen, K. 2013 Modelling sedimentation-consolidation in the framework of a one-dimensional two-phase flow model. J. Hydraul Res. 51 (3), 293–305.CrossRefGoogle Scholar
Chauchat, J., Revil-Baudard, T. & Hurther, D. 2015 An improved two-phase flow model for steady uniform sheet-flow based on dense granular flow rheology. In 36th IAHR World Congress, The Hague.Google Scholar
Chiodi, F., Claudin, P. & Andreotti, B. 2014 A two-phase flow model of sediment transport: transition from bedload to suspended load. J. Fluid Mech. 755, 561–581.CrossRefGoogle Scholar
Courrech du Pont, S., Gondret, P., Perrin, B. & Rabaud, M. 2003 Granular avalanches in fluids. Phys. Rev. Lett. 90, 044301.CrossRefGoogle ScholarPubMed
Cowen, E. A., Dudley, R. D., Liao, Q., Variano, E. A. & Liu, P. L.-F. 2010 An in situ borescopic quantitative imaging profiler for the measurement of high concentration sediment velocity. Exp. Fluids 49 (1), 77–88.CrossRefGoogle Scholar
Da Cruz, F., Chevoir, F., Roux, J. N. & Iordanoff, I. 2004 Macroscopic friction of dry granular materials. In Transient Processes in Tribology (ed. Dalmaz, G., Lubrecht, A. A., Dowson, D. & Priest, M.), Tribology and Interface Engineering Series, vol. 43, pp. 53–61; 30th Leeds–Lyon Symposium on Tribology, Inst. Natl Sci. Appl., Lyon, France, 2–5 September 2003, Elsevier.Google Scholar
Da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72, 021309.Google ScholarPubMed
Dallavalle, J. M. 1948 Micrometrics: The Technology of Fine Particles, 2nd edn. Pitman Publishing Corporation.Google Scholar
Doppler, D., Gondret, P., Loiseleux, T., Meyer, S. & Rabaud, M. 2007 Relaxation dynamics of water-immersed granular avalanches. J. Fluid Mech. 577, 161–181.CrossRefGoogle Scholar
Duran, O., Andreotti, B. & Claudin, P. 2012 Numerical simulation of turbulent sediment transport, from bed load to saltation. Phys. Fluids 24 (10), 103306.CrossRefGoogle Scholar
Einstein, H. A. 1942 Formulas for the transport of bed sediment. Trans. ASCE 107, 561–574.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40 (1), 1–24.CrossRefGoogle Scholar
Fredsøe, J. & Deigaard, R. 1992 Mechanics of Coastal Sediment Transport. World Scientific.CrossRefGoogle Scholar
Frey, P. 2014 Particle velocity and concentration profiles in bedload experiments on a steep slope. Earth Surf. Process. Landf. 39 (5), 646–655.CrossRefGoogle Scholar
Frey, P. & Church, M. 2009 How river beds move. Science 325, 1509–1510.CrossRefGoogle ScholarPubMed
Frey, P. & Church, M. 2011 Bedload: a granular phenomenon. Earth Surf. Process. Landf. 36, 58–69.CrossRefGoogle Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35 (1), 267–293.CrossRefGoogle Scholar
Goldhirsch, I. 2010 Stress, stress asymmetry and couple stress: from discrete particles to continuous fields. Granul. Matt. 12 (3), 239–252.CrossRefGoogle Scholar
Hergault, V., Frey, P., Métivier, F., Barat, C., Ducottet, C., Böhm, T. & Ancey, C. 2010 Image processing for the study of bedload transport of two-size spherical particles in a supercritical flow. Exp. Fluids 49 (5), 1095–1107.CrossRefGoogle Scholar
Holyoake, A. J. & Mcelwaine, J. N. 2012 High-speed granular chute flows. J. Fluid Mech. 710, 35–71.CrossRefGoogle Scholar
Houssais, M., Ortiz, C. P., Durian, D. J. & Jerolmack, D. J. 2015 Onset of sediment transport is a continuous transition driven by fluid shear and granular creep. Nature Communications 6, 6527.CrossRefGoogle ScholarPubMed
Hsu, T. J., Jenkins, J. T. & Liu, P. L. F. 2004 On two-phase sediment transport: sheet flow of massive particles. Proc. R. Soc. Lond. A 460 (2048), 2223–2250.CrossRefGoogle Scholar
Izard, E., Bonometti, T. & Lacaze, L. 2014 Simulation of an avalanche in a fluid with a soft-sphere/immersed boundary method including a lubrication force. J. Comput. Multiphase Flows 6 (4), 391–406.CrossRefGoogle Scholar
Jackson, R. 2000 The Dynamics of Fluidized Particles. Cambridge University Press.Google Scholar
Jenkins, J. T. 2006 Dense shearing flows of inelastic disks. Phys. Fluids 18 (10), 103307.CrossRefGoogle Scholar
Jenkins, J. T. 2007 Dense inclined flows of inelastic spheres. Granul. Matt. 10 (1), 47–52.CrossRefGoogle Scholar
Jenkins, J. T. & Hanes, D. M. 1998 Collisional sheet flows of sediment driven by a turbulent fluid. J. Fluid Mech. 370, 29–52.CrossRefGoogle Scholar
Ji, C., Munjiza, A., Avital, E., Ma, J. & Williams, J. J. R. 2013 Direct numerical simulation of sediment entrainment in turbulent channel flow. Phys. Fluids 25 (5), 056601.CrossRefGoogle Scholar
Jop, P. 2015 Rheological properties of dense granular flows. C. R. Phys. 16 (1), 62–72.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.CrossRefGoogle ScholarPubMed
Kamrin, K. & Koval, G. 2012 Nonlocal constitutive relation for steady granular flow. Phys. Rev. Lett. 108, 178301.Google ScholarPubMed
Kidanemariam, A. G. & Uhlmann, M. 2014 Interface-resolved direct numerical simulation of the erosion of a sediment bed sheared by laminar channel flow. Intl J. Multiphase Flow 67 (0), 174–188.CrossRefGoogle Scholar
Komatsu, T. S., Inagaki, S., Nakagawa, N. & Nasuno, S. 2001 Creep motion in a granular pile exhibiting steady surface flow. Phys. Rev. Lett. 86, 1757–1760.CrossRefGoogle Scholar
Lajeunesse, E., Malverti, L. & Charru, F. 2010 Bed load transport in turbulent flow at the grain scale: experiments and modeling. J. Geophys. Res. 115, F04001.Google Scholar
Larcher, M., Fraccarollo, L., Armanini, A. & Capart, H. 2007 Set of measurement data from flume experiments on steady uniform debris flows. J. Hydraul Res. 45, 59–71.CrossRefGoogle Scholar
Lee, C.-H., Low, Y. M. & Chiew, Y.-M. 2016 Multi-dimensional rheology-based two-phase model for sediment transport and applications to sheet flow and pipeline scour. Phys. Fluids 28 (5), 053305.CrossRefGoogle Scholar
Li, L. & Sawamoto, M. 1995 Multi-phase model on sediment transport in sheet-flow regime under oscillatory flow. Coast. Engng Japan 38, 157–178.CrossRefGoogle Scholar
Lois, G., Lemaître, A. & Carlson, J. M. 2006 Emergence of multi-contact interactions in contact dynamics simulations of granular shear flows. Europhys. Lett. 76 (2), 318–324.CrossRefGoogle Scholar
Maurin, R.2015 Investigation of granular behavior in bedload transport using an Eulerian–Lagrangian model. PhD thesis, Université Grenoble Alpes.Google Scholar
Maurin, R., Chauchat, J., Chareyre, B. & Frey, P. 2015 A minimal coupled fluid–discrete element model for bedload transport. Phys. Fluids 27 (11), 113302.CrossRefGoogle Scholar
Meyer-Peter, E. & Müller, R. 1948 Formulas for bed-load transport. In Proceedings of the 2nd Meeting, pp. 39–64. IAHR.Google Scholar
Midi, G. D. R. 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Mouilleron, H., Charru, F. & Eiff, O. 2009 Inside the moving layer of a sheared granular bed. J. Fluid Mech. 628, 229–239.CrossRefGoogle Scholar
Ouriemi, M., Aussillous, P. & Guazzelli, E. 2009 Sediment dynamics. Part 1. Bed-load transport by laminar shearing flows. J. Fluid Mech. 636, 295–319.CrossRefGoogle Scholar
Prandtl, L. 1926 Bericht über neuere Turbulenzforschung. Hydraulische Probleme. Vorträge Hydrauliktagung Göttingen 5, 1–13.Google Scholar
Revil-Baudard, T. & Chauchat, J. 2013 A two-phase model for sheet flow regime based on dense granular flow rheology. J. Geophys. Res. 118 (2), 619–634.CrossRefGoogle Scholar
Revil-Baudard, T., Chauchat, J., Hurther, D. & Barraud, P.-A. 2015 Investigation of sheet-flow processes based on novel acoustic high-resolution velocity and concentration measurements. J. Fluid Mech. 767, 1–30.CrossRefGoogle Scholar
Richard, P., Valance, A., Métayer, J.-F., Sanchez, P., Crassous, J., Louge, M. & Delannay, R. 2008 Rheology of confined granular flows: scale invariance, glass transition, and friction weakening. Phys. Rev. Lett. 101, 248002.CrossRefGoogle ScholarPubMed
Richardson, J. F. & Zaki, W. N. 1954 Sedimentation and fluidization: part I. Trans. Inst. Chem. Engrs 32, 35–53.Google Scholar
Rondon, L., Pouliquen, O. & Aussillous, P. 2011 Granular collapse in a fluid: role of the initial volume fraction. Phys. Fluids 23 (7), 073301.CrossRefGoogle Scholar
Roux, J.-N. & Combe, G. 2002 Quasistatic rheology and the origins of strain. C. R. Phys. 3 (2), 131–140.CrossRefGoogle Scholar
Schwager, T. & Pöschel, T. 2007 Coefficient of restitution and linear spring–dashpot model revisited. Granul. Matt. 9, 465–469.CrossRefGoogle Scholar
Šmilauer, V., Catalano, E., Chareyre, B., Dorofeenko, S., Duriez, J., Dyck, N., Elias, J., Er, B., Eulitz, A., Gladky, A. et al. 2015 Yade Documentation, 2nd edn. The Yade Project (http://yade-dem.org/doc/) doi:10.5281/zenodo.34073.CrossRefGoogle Scholar
Sumer, B. M., Kozakiewicz, A., Fredsøe, J. & Deigaard, R. 1996 Velocity and concentration profiles in sheet-flow layer of movable bed. J. Hydraul. Engng ASCE 122 (10), 549–558.CrossRefGoogle Scholar
Trulsson, M., Andreotti, B. & Claudin, P. 2012 Transition from the viscous to inertial regime in dense suspensions. Phys. Rev. Lett. 109, 118305.CrossRefGoogle ScholarPubMed