Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T07:18:10.329Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformation characteristics of a single droplet driven by a piezoelectric nozzle of the drop-on-demand inkjet system

Published online by Cambridge University Press:  02 May 2019

Shangkun Wang ,
Yonghong Zhong  and
Haisheng Fang Open the ORCID record for Haisheng Fang [Opens in a new window]
Shangkun Wang
Affiliation:
State Key Laboratory of Coal Combustion, School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, 430074, China
Yonghong Zhong
Affiliation:
State Key Laboratory of Coal Combustion, School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, 430074, China
Haisheng Fang*
Affiliation:
State Key Laboratory of Coal Combustion, School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, 430074, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the drop-on-demand (DOD) inkjet system, deformation process and the direct relations between the droplet motions and the liquid properties have been seldom investigated, although they are very critical for the printing accuracy. In this study, experiments and computational simulations regarding deformation of a single droplet driven by a piezoelectric nozzle have been conducted to address the deformation characteristics of droplets. It is found that the droplet deformation is influenced by the pressure wave propagation in the ink channel related to the driven parameters and reflected in the subsequent droplet motions. 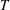The deformation extent oscillates with a certain period of $T$ and a decreasing amplitude as the droplet moves downwards. The deformation extent is found strongly dependent on the capillary number (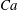$Ca$), first ascending and then descending as the number increases. The maximum value of the deformation extent is surprisingly found to be within range of 0.068–0.082 of the 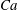$Ca$ number regardless of other factors. Furthermore, the Rayleigh’s linear relation of the oscillation frequency of the droplet to the parameter, 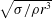$\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}r^{3}}$ (where $\unicode[STIX]{x1D70E}$ is the surface tension coefficient, 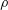$\unicode[STIX]{x1D70C}$ is the density and $r$ is the droplet’s radius), is updated with a smaller slope shown both by experiment and simulation.

JFM classification

Drops and Bubbles: Drops Micro-/Nano-fluid dynamics: Microfluidics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 634 - 645
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Becker, E., Hiller, W. J. & Kowalewski, T. A. 1991 Experimental and theoretical investigation of large-amplitude oscillations of liquid droplets. J. Fluid Mech. 231, 189–210.10.1017/S0022112091003361Google Scholar
Bogy, D. B. & Talke, F. E. 1984 Experimental and theoretical-study of wave-propagation phenomena in drop-on-demand ink jet devices. IBM J. Res. Dev. 28 (3), 314–321.10.1147/rd.283.0314Google Scholar
De Gans, B. J., Duineveld, P. C. & Schubert, U. S. 2004 Inkjet printing of polymers: state of the art and future developments. Adv. Mater. 16 (3), 203–213.10.1002/adma.200300385Google Scholar
Derby, B. 2011 Inkjet printing ceramics: From drops to solid. J. Eur. Ceram. Soc. 31 (14), 2543–2550.10.1016/j.jeurceramsoc.2011.01.016Google Scholar
Dijksman, J. F., Duineveld, P. C., Hack, M. J. J., Pierik, A., Rensen, J., Rubingh, J.-E., Schram, I. & Vernhout, M. M. 2007 Precision ink jet printing of polymer light emitting displays. J. Mater. Chem. 17 (6), 511–522.10.1039/B609204GGoogle Scholar
Fromm, J. E. 1984 Numerical calculation of the fluid dynamics of drop-on-demand jets. IBM J. Res. Dev. 28 (3), 322–333.10.1147/rd.283.0322Google Scholar
Kamyshny, A. 2011 Metal-based Inkjet Inks for Printed Electronics. Open Appl. Phys. J. 4 (1), 19–36.10.2174/1874183501104010019Google Scholar
Kornek, U., Müller, F., Harth, K., Hahn, A., Ganesan, S., Tobiska, L. & Stannarius, R. 2010 Oscillations of soap bubbles. New J. Phys. 12, 073031.10.1088/1367-2630/12/7/073031Google Scholar
McKerricher, G., Vaseem, M. & Shamim, A. 2017 Fully inkjet-printed microwave passive electronics. Microsystems & Nanoengineering 3 (2016), 16075.10.1038/micronano.2016.75Google Scholar
Olsson, E. & Kreiss, G. 2005 A conservative level set method for two phase flow. J. Comput. Phys. 210 (1), 225–246.Google Scholar
Olsson, E., Kreiss, G. & Zahedi, S. 2007 A conservative level set method for two phase flow II. J. Comput. Phys. 225 (1), 785–807.10.1016/j.jcp.2006.12.027Google Scholar
Rayleigh, L. 1879 On the Capillary Phenomena of Jets. Proc. R. Soc. Lond. 29 (196–199), 71–97.Google Scholar
Rein, M. 1993 Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 12 (2), 61–93.10.1016/0169-5983(93)90106-KGoogle Scholar
Reis, N., Ainsley, C. & Derby, B. 2005 Ink-jet delivery of particle suspensions by piezoelectric droplet ejectors. J. Appl. Phys. 97 (9), 094903.10.1063/1.1888026Google Scholar
Saunders, R. E. & Derby, B. 2014 Inkjet printing biomaterials for tissue engineering: bioprinting. Intl Mater. Rev. 59 (8), 430–448.10.1179/1743280414Y.0000000040Google Scholar
Shin, W. J., Jeong, Y. S., Choi, K. & Shin, W. G. 2015 The effect of inkjet operating parameters on the size control of aerosol particles. Aerosol Sci. Technol. 49 (12), 1256–1262.10.1080/02786826.2015.1115465Google Scholar
Wijshoff, H.2006 Manipulating drop formation in piezo acoustic inkjet. In NIP & Digital Fabrication Conference, vol. 2006, no. 1, pp. 79–82.Google Scholar
Wijshoff, H. 2010 The dynamics of the piezo inkjet printhead operation. Phys. Rep. 491 (4–5), 77–177.Google Scholar
Yun, S. 2017 Bouncing of an ellipsoidal drop on a superhydrophobic surface. Sci. Rep. 7 (1), 17699.10.1038/s41598-017-18017-2Google Scholar
Zhang, X. 1999 Dynamics of growth and breakup of viscous pendant drops into air. J. Colloid Interface Sci. 212 (1), 107–122.10.1006/jcis.1998.6047Google Scholar
Zhong, Y., Fang, H., Ma, Q. & Dong, X. 2018 Analysis of droplet stability after ejection from an inkjet nozzle. J. Fluid Mech. 845, 378–391.10.1017/jfm.2018.251Google Scholar