Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T00:09:29.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of the temporal growth rate in linear instability of compressible gas flows

Published online by Cambridge University Press:  31 July 2015

Mario Weder ,
Michael Gloor  and
Leonhard Kleiser
Mario Weder*
Affiliation:
Institute of Fluid Dynamics, ETH Zurich, 8092 Zurich, Switzerland Institute of Mechanical Systems, ETH Zurich, 8092 Zurich, Switzerland
Michael Gloor
Affiliation:
Institute of Fluid Dynamics, ETH Zurich, 8092 Zurich, Switzerland
Leonhard Kleiser
Affiliation:
Institute of Fluid Dynamics, ETH Zurich, 8092 Zurich, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a decomposition of the temporal growth rate 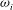${\it\omega}_{i}$ which characterises the evolution of wave-like disturbances in linear stability theory for compressible flows. The decomposition is based on the disturbance energy balance by Chu (Acta Mech., vol. 1 (3), 1965, pp. 215–234) and provides terms for production, dissipation and flux of energy as components of 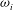${\it\omega}_{i}$. The inclusion of flux terms makes our formulation applicable to unconfined flows and flows with permeable or vibrating boundaries. The decomposition sheds light on the fundamental mechanisms determining temporal growth or decay of disturbances. The additional insights gained by the proposed approach are demonstrated by an investigation of two model flows, namely compressible Couette flow and a plane compressible jet.

JFM classification

Compressible Flows: Compressible Flows Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 120 - 132
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th edn. National Bureau of Standards.Google Scholar
Bayliss, A. & Turkel, E. 1992 Mappings and accuracy for Chebyshev pseudo-spectral approximations. J. Comput. Phys. 101 (2), 349–359.Google Scholar
Busemann, A. 1935 Gasströmung mit laminarer Grenzschicht entlang einer Platte. Z. Angew. Math. Mech. 15 (1–2), 23–25.CrossRefGoogle Scholar
Chu, B.-T. 1965 On the energy transfer to small disturbances in fluid flow (Part I). Acta Mech. 1 (3), 215–234.Google Scholar
Criminale, W. O., Jackson, T. L. & Joslin, R. D. 2003 Theory and Computation of Hydrodynamic Stability, 1st edn. Cambridge University Press.Google Scholar
Drazin, P. D. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge Mathematical Library.CrossRefGoogle Scholar
Duck, P. W., Erlebacher, G. & Hussaini, M. Y. 1994 On the linear stability of compressible plane Couette flow. J. Fluids Mech. 258, 131–165.CrossRefGoogle Scholar
Hu, S. & Zhong, X. 1998 Linear stability of viscous supersonic plane Couette flow. Phys. Fluids 10 (3), 709–729.CrossRefGoogle Scholar
Malik, M., Alam, M. & Dey, J. 2006 Nonmodal energy growth and optimal perturbations in compressible plane Couette flow. Phys. Fluids 18 (3), 034103.Google Scholar
Malik, M., Dey, J. & Alam, M. 2008 Linear stability, transient energy growth, and the role of viscosity stratification in compressible plane Couette flow. Phys. Rev. E 77 (3).CrossRefGoogle ScholarPubMed
Malik, M. R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86 (2), 376–413.CrossRefGoogle Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.Google Scholar
Moran, M. J. & Shapiro, H. N. 2000 Fundamentals of Engineering Thermodynamics, 4th edn. Wiley.Google Scholar
Parras, L. & Le Dizès, S. 2010 Temporal instability modes of supersonic round jets. J. Fluid Mech. 662, 173–196.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow, Applied Mathematical Sciences, vol. 148. Springer.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, 1st edn. vol. 142. Springer.CrossRefGoogle Scholar
Tam, C. K. W. & Hu, F. Q. 1989 On the three families of instability waves of high-speed jets. J. Fluid Mech. 201, 447–483.Google Scholar
Thompson, K. W. 1987 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 68 (1), 1–24.Google Scholar
Tritarelli, R. C.2011 Modal and non-modal energy evolution in hypersonic boundary layers over porous coatings. Master’s thesis, ETH Zurich.Google Scholar