Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T18:05:35.830Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical slope for laminar transcritical shallow-water flows

Published online by Cambridge University Press:  13 October 2015

O. Thual ,
L. Lacaze ,
M. Mouzouri  and
B. Boutkhamouine
O. Thual*
Affiliation:
Université de Toulouse; INPT, UPS; IMFT, Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
L. Lacaze
Affiliation:
Université de Toulouse; INPT, UPS; IMFT, Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
M. Mouzouri
Affiliation:
Université de Toulouse; INPT, UPS; IMFT, Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
B. Boutkhamouine
Affiliation:
Université de Toulouse; INPT, UPS; IMFT, Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Backwater curves denote the depth profiles of steady flows in a shallow open channel. The classification of these curves for turbulent regimes is commonly used in hydraulics. When the bottom slope 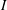$I$ is increased, they can describe the transition from fluvial to torrential regimes. In the case of an infinitely wide channel, we show that laminar flows have the same critical height 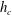$h_{c}$ as that in the turbulent case. This feature is due to the existence of surface slope singularities associated to plug-like velocity profiles with vanishing boundary-layer thickness. We also provide the expression of the critical surface slope as a function of the bottom curvature at the critical location. These results validate a similarity model to approximate the asymptotic Navier–Stokes equations for small slopes 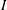$I$ with Reynolds number 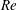$Re$ such that 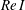$Re\,I$ is of order 1.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Low-Reynolds-number flows Interfacial Flows (free surface): Thin films
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , R1
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseenko, S. V., Nakoryakov, V. Ye. & Pokusaev, B. G. 1985 Wave formation on a vertical falling liquid film. AIChE J. 31 (9), 1446–1460.Google Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45 (2), 50–155.Google Scholar
Boutounet, M., Chupin, L., Noble, P. & Vila, J.-P. 2008 Shallow water viscous flows for arbitrary topopgraphy. Commun. Math. Sci. 6 (1), 29–55.Google Scholar
Bukreev, V. I., Gusev, A. V. & Lyapidevskii, V. Yu. 2002 Transcritical flow over a ramp in an open channel. Fluid Dyn. 37 (6), 896–902.Google Scholar
Chakraborty, S., Nguyen, P.-K., Ruyer-Quil, C. & Bontozoglou, V. 2014 Extreme solitary waves on falling liquid films. J. Fluid Mech. 745, 564–591.Google Scholar
Chow, V. T. 1959 Open-channel Hydraulics. McGraw-Hill.Google Scholar
Fernàndez-Nieto, E. D., Noble, P. & Vila, J.-P. 2010 Shallow water equations for non-newtonian fluids. J. Non-Newtonian Fluid Mech. 165 (1314), 712–732.CrossRefGoogle Scholar
Gjevik, B. 1970 Occurrence of finite amplitude surface waves on falling liquid films. Phys. Fluids 13 (8), 1918–1925.CrossRefGoogle Scholar
Kapitsa, P. L. & Kapitsa, S. P. 1949 Wave flow of thin layers of a viscous liquid. Zh. Eksp. Teor. Fiz. 19, 105–120.Google Scholar
Lin, S. P. 1969 Finite-amplitude stability of a parallel flow with a free surface. J. Fluid Mech. 36, 113–126.Google Scholar
Nakaya, C. 1975 Long waves on a thin fluid layer flowing down an inclined plane. Phys. Fluids 18 (11), 1407–1412.Google Scholar
Nguyen, L. T. & Balakotaiah, V. 2000 Modeling and experimental studies of wave evolution on free falling viscous films. Phys. Fluids 12 (9), 2236–2256.CrossRefGoogle Scholar
Noble, P. & Vila, J.-P. 2013 Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations. J. Fluid Mech. 735, 29–60.Google Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.CrossRefGoogle Scholar
Pumir, A., Manneville, P. & Pomeau, Y. 1983 On solitary waves running down an inclined plane. J. Fluid Mech. 135, 27–50.Google Scholar
Roberts, A.J. 1996 Low-dimensional models of thin film fluid dynamics. Phys. Lett. A 212 (12), 63–71.Google Scholar
Ruyer-Quil, C. & Manneville, P. 1998 Modeling film flows down inclined planes. Eur. Phys. J. B 6 (2), 277–292.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15 (2), 357–369.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2005 On the speed of solitary waves running down a vertical wall. J. Fluid Mech. 531, 181–190.CrossRefGoogle Scholar
Sadiq, I. M. R. & Usha, R. 2008 Thin newtonian film flow down a porous inclined plane: stability analysis. Phys. Fluids 20 (2), 022105.Google Scholar
de Saint-Venant, B. 1871 Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et à l’introduction des marées dans leur lit. C. R. Acad. Sci. Paris 73, 147–154.Google Scholar
Samanta, A., Ruyer-Quil, C. & Goyeau, B. 2011 A falling film down a slippery inclined plane. J. Fluid Mech. 684, 353–383.Google Scholar
Schlichting, H. 1955 Boundary-layer Theory. McGraw-Hill.Google Scholar
Scilab Enterprises 2012 Scilab: Free and Open Source Software for Numerical Computation, Scilab Enterprises, (http://www.scilab.org).Google Scholar
Serre, F. 1953 Contribution à l’étude des écoulements permanents et variables dans les canaux (Contribution to the study of steady and unsteady channel flows). La Houille Blanche 8, 830–887.CrossRefGoogle Scholar
Shkadov, V. Y. 1967 Wave flow regimes of a thin layer of viscous fluid subject to gravity. Fluid Dyn. 2 (1), 29–34.Google Scholar
Shkadov, V. Y. & Sisoev, G. M. 2004 Waves induced by instability in falling films of finite thickness. Fluid Dyn. Res. 35 (5), 357–389.CrossRefGoogle Scholar
Thual, O. 2013 Modelling rollers for shallow water flows. J. Fluid Mech. 728, 1–4.Google Scholar
Thual, O., Plumerault, L.-R. & Astruc, D. 2010 Linear stability of the 1d Saint-Venant equations and drag parameterizations. J. Hydraul Res. 48 (3), 348–353.CrossRefGoogle Scholar
Zerihun, Y. T. & Fenton, J. D. 2006 One-dimensional simulation model for steady transcritical free surface flows at short length transitions. Adv. Water Resour. 29 (11), 1598–1607.Google Scholar