Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T13:37:27.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Correlation coefficients of thermodynamic fluctuations in compressible aerodynamic turbulence

Published online by Cambridge University Press:  25 July 2018

G. A. Gerolymos Open the ORCID record for G. A. Gerolymos [Opens in a new window]  and
I. Vallet Open the ORCID record for I. Vallet [Opens in a new window]
G. A. Gerolymos
Affiliation:
Sorbonne Université, Faculty of Science and Engineering, 4 place Jussieu, 75005 Paris, France
I. Vallet*
Affiliation:
Sorbonne Université, Faculty of Science and Engineering, 4 place Jussieu, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Thermodynamic fluctuations of pressure, density, temperature or entropy $\{p^{\prime },\unicode[STIX]{x1D70C}^{\prime },T^{\prime },s^{\prime }\}$ in compressible aerodynamic turbulence, although generated by the flow, are fundamentally related to one another by the thermodynamic equation of state. Ratios between non-dimensional root-mean-square (r.m.s.) levels (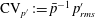$\text{CV}_{p^{\prime }}:=\bar{p}^{-1}\,p_{rms}^{\prime }$, 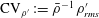$\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }}:=\bar{\unicode[STIX]{x1D70C}}^{-1}\,\unicode[STIX]{x1D70C}_{rms}^{\prime }$, 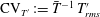$\text{CV}_{T^{\prime }}:=\bar{T}^{-1}\,T_{rms}^{\prime }$), along with all possible 2-moment correlation coefficients 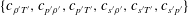$\{c_{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }},c_{p^{\prime }\unicode[STIX]{x1D70C}^{\prime }},c_{p^{\prime }T^{\prime }},c_{s^{\prime }\unicode[STIX]{x1D70C}^{\prime }},c_{s^{\prime }T^{\prime }},c_{s^{\prime }p^{\prime }}\}$, represent, in the sense of Bradshaw (Annu. Rev. Fluid Mech., vol. 9, 1977, pp. 33–54), the thermodynamic turbulence structure of the flow. We use direct numerical simulation (DNS) data, both for plane channel flow and for sustained homogeneous isotropic turbulence, to determine the range of validity of the leading-order, formally 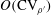$O(\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }})$, approximations of the exact relations between thermodynamic turbulence structure parameters. Available DNS data are mapped on the 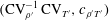$(\text{CV}_{\unicode[STIX]{x1D70C}^{\prime }}^{-1}\,\text{CV}_{T^{\prime }},c_{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }})$-plane and their loci, identified using the leading-order approximations, highlight specific behaviour for different flows or flow regions. For the particular case of sustained compressible homogeneous isotropic turbulence, it is shown that the DNS data collapse onto a single curve corresponding to 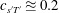$c_{s^{\prime }T^{\prime }}\approxeq 0.2$ (for air flow), while the approximation 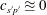$c_{s^{\prime }p^{\prime }}\approxeq 0$ fits reasonably well wall turbulence DNS data, providing building blocks towards the construction of simple phenomenological models.

JFM classification

Compressible Flows: Compressible boundary layers Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 447 - 478
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banerjee, S. & Galtier, S. 2014 A Kolomogorov-like exact relation for compressible polytropic turbulence. J. Fluid Mech. 542, 230–242.Google Scholar
Barre, S. & Bonnet, J. P. 2015 Detailed experimental study of a highly compressible supersonic turbulent plane mixing layer and comparison with most recent DNS results: ‘towards an accurate description of compressibility effects in supersonic free shear flows’. Intl J. Heat Fluid Flow 51, 324–334.Google Scholar
Blaisdell, G. A., Mansour, N. N. & Reynolds, W. C. 1993 Compressibility effects on the growth and structure of homogeneous turbulent shear flow. J. Fluid Mech. 256, 443–485.Google Scholar
Bradshaw, P. 1977 Compressible turbulent shear layers. Annu. Rev. Fluid Mech. 9, 33–54.Google Scholar
Chu, B. T. & Kovásznay, L. S. G. 1958 Nonlinear interactions in a viscous heat-conducting compressible gas. J. Fluid Mech. 3, 494–514.Google Scholar
Coleman, G. N., Kim, J. & Moser, R. D. 1995 A numerical study of turbulent supersonic isothermal-wall channel flow. J. Fluid Mech. 305, 159–183.Google Scholar
Donzis, D. A. & Jagannathan, S. 2013 Fluctuation of thermodynamic variables in stationary compressible turbulence. J. Fluid Mech. 733, 221–244.Google Scholar
Duan, L., Choudhari, M. M. & Zhang, C. 2016 Pressure fluctuations induced by a hypersonic turbulent boundary-layer. J. Fluid Mech. 804, 578–607.Google Scholar
Duan, L. & Martín, M. P. 2011 Direct numerical simulation of hypersonic turbulent boundary-layers. Part 4. Effect of high enthalpy. J. Fluid Mech. 684, 25–59.Google Scholar
Eswaran, V. & Pope, S. B. 1988 An examination of forcing in DNS of turbulence. Comput. Fluids 16 (3), 257–278.Google Scholar
Foysi, H., Sarkar, S. & Friedrich, R. 2004 Compressibility effects and turbulence scalings in supersonic channel flow. J. Fluid Mech. 509, 207–216.Google Scholar
Gatski, T. B. & Bonnet, J.-P. 2009 Compressibility, Turbulence and High Speed Flow. Elsevier.Google Scholar
Gerolymos, G. A., Sénéchal, D. & Vallet, I. 2010 Performance of very-high-order upwind schemes for DNS of compressible wall-turbulence. Intl J. Numer. Meth. Fluids 63, 769–810.Google Scholar
Gerolymos, G. A., Sénéchal, D. & Vallet, I. 2013 Wall effects on pressure fluctuations in turbulent channel flow. J. Fluid Mech. 720, 15–65.Google Scholar
Gerolymos, G. A. & Vallet, I. 1996 Implicit computation of the 3-D compressible Navier–Stokes equations using k-𝜀 turbulence closure. AIAA J. 34 (7), 1321–1330.Google Scholar
Gerolymos, G. A. & Vallet, I. 2014 Pressure, density, temperature and entropy fluctuations in compressible turbulent plane channel flow. J. Fluid Mech. 757, 701–746.Google Scholar
Guarini, S. E., Moser, R. D., Shariff, K. & Wray, A. 2000 Direct numerical simulation of a supersonic turbulent boundary-layer at Mach 2.5. J. Fluid Mech. 414, 1–33.Google Scholar
Hansen, C. F.1958 Approximations for the thermodynamic and transport properties of high-temperature air. Tech. Note 4150. NACA, Ames Aeronautical Laboratory, Moffett Field, CA, USA.Google Scholar
Huang, P. G., Coleman, G. N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.Google Scholar
Jagannathan, S. & Donzis, D. A. 2016 Reynolds and mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations. J. Fluid Mech. 789, 669–707.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel-flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kistler, A. L. 1959 Fluctuation measurements in a supersonic turbulent boundary-layer. Phys. Fluids 2, 290–297.Google Scholar
Kovásznay, L. S. G. 1953 Turbulence in supersonic flow. J. Aero. Sci. 20, 657–674; 682.Google Scholar
Laderman, A. J. & Demetriades, A. 1974 Mean and fluctuating flow measurements in the hypersonic boundary-layer over a cooled wall. J. Fluid Mech. 63, 121–144.Google Scholar
Lagha, M., Kim, J., Eldredge, J. D. & Zhong, X. 2011 Near-wall dynamics of compressible boundary layers. Phys. Fluids 23, 065109(1–13).Google Scholar
Lechner, R., Sesterhenn, J. & Friedrich, R. 2001 Turbulent supersonic channel flow. J. Turbul. 2, 001.1–25.Google Scholar
Lee, S., Lele, S. K. & Moin, P. 1991 Eddy shocklets in decaying compressible turbulence. Phys. Fluids A 3 (4), 657–664.Google Scholar
Lele, S. K. 1994 Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 26, 211–254.Google Scholar
Liepmann, H. W. & Roshko, A. 1957 Elements of Gasdynamics. John Wiley.Google Scholar
Mahesh, K., Lele, S. K. & Moin, P. 1997 The influence of entropy fluctutions on the interaction of turbulence with a shock-wave. J. Fluid Mech. 334, 353–379.Google Scholar
Modesti, D. & Pirozzoli, S. 2016 Reynolds and Mach number effects in compressible turbulent channel. Intl J. Heat Fluid Flow 59 (33–49).Google Scholar
Morkovin, M. V. 1962 Effects of compressibility on turbulent flows. In Mechanics of Turbulence (Proceedings of the International Colloquium, Aug. 28–Sep. 2, 1961, Marseille, [Fra]) (ed. Favre, A.), Colloques Internationaux du CNRS 108, pp. 367–380. Editions du CNRS.Google Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.Google Scholar
Pham, H.(Ed.) 2006 Handbook of Engineering Statistics. Springer.Google Scholar
Ristorcelli, J. R. 1997 A pseudosound constitutive relationship for the dilatational covariances in compressible turbulence. J. Fluid Mech. 347, 37–70.Google Scholar
Rubesin, M. W.1976 A 1-equation model of turbulence for use with the compressible Navier–Stokes equations. Tech. Mem. NASA–1976–TM–X–73128. NASA, Ames Research Center, Moffett Field, CA, USA.Google Scholar
Sarkar, S. 1995 The stabilizing effect of compressibility in turbulent shear flow. J. Fluid Mech. 282, 163–186.Google Scholar
Shadloo, M. S., Hadjadj, A. & Hussain, F. 2015 Statistical behavior of supersonic turbulent boundary layers with heat transfer at m ∞ = 2. Intl J. Heat Fluid Flow 53, 113–134.Google Scholar
Smits, A. J. & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer.Google Scholar
Suman, S. & Girimaji, S. S. 2001 Dynamical model for velocity-gradient evolution in compressible turbulence. J. Fluid Mech. 683, 289–319.Google Scholar
Taulbee, D. & Van Osdol, J.1991 Modeling turbulent compressible flows: the mass fluctuating velocity and squared density. AIAA Paper 1991–0524 (doi: http://dx.doi.org/10.2514/6.1991-524).Google Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scalings in high-Reynolds-number turbulent boundary-layers. J. Fluid Mech. 585, 1–40.Google Scholar
Wang, J., Shi, Y., Wang, L.-P. & He, X. 2011 Effect of shocklets on the velocity gradients in highly compressible isotropic turbulence. Phys. Fluids 23, 125103.Google Scholar
Wei, L. & Pollard, A. 2011 Interactions among pressure, density, vorticity and their gradients in compressible turbulent channel flow. J. Fluid Mech. 673, 1–18.Google Scholar
Zhang, Y. S., Bi, W. T., Hussain, F. & She, Z. S. 2013 A generalized Reynolds analogy for compressible wall-boundaed turbulent flows. J. Fluid Mech. 739, 392–420.Google Scholar