Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T11:03:48.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Corner effects for oblique shock wave/turbulent boundary layer interactions in rectangular channels

Published online by Cambridge University Press:  16 January 2019

X. Xiang Open the ORCID record for X. Xiang [Opens in a new window]  and
H. Babinsky
X. Xiang*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
H. Babinsky
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In a rectangular cross-section wind tunnel, a separated oblique shock reflection is set to interact with the turbulent boundary layer (oblique shock wave/turbulent boundary layer interaction (SBLI)) both on the bottom wall and in the corners formed by the intersection of the floor with the sidewalls. To examine how corner separations can affect the ‘quasi-two-dimensional’ main interaction and by what mechanisms this is achieved, an experimental investigation has been conducted. This examines how modifications to the corner separation affect an 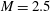$M=2.5$ oblique shock reflection. The nature of the flow field is studied using flow visualisation, pressure-sensitive paint and laser Doppler anemometry. The results show that the size and shape of central separation vary considerably when the onset and magnitude of corner separation changes. The primary mechanism explaining the coupling between these separated regions appears to be the generation of compression waves and expansion fans as a result of the displacement effect of the corner separation. This is shown to modify the three-dimensional shock structure and alter the adverse pressure gradient experienced by the tunnel floor boundary layer. It is suggested that a typical oblique SBLI in rectangular channels features several zones depending on the relative position of the corner waves and the main interaction domain. In particular, it has been shown that the position of the corner ‘shock’ crossing point, found by approximating the corner compression waves by a straight line, is a critical factor determining the main separation size and shape. Thus, corner effects can substantially modify the central separation. This can cause significant growth or contraction of the separation length measured along the symmetry line from the nominally two-dimensional baseline value, giving a fivefold increase from the smallest to the largest observed value. Moreover, the shape and flow topology of the centreline separation bubble is also considerably changed by varying corner effects.

JFM classification

Boundary Layers: Boundary layer separation Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 1060 - 1083
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamson, T. C. & Messiter, A. F. 1980 Analysis of two-dimensional interactions between shock waves and boundary layers. Annu. Rev. Fluid Mech. 12 (1), 103–138.Google Scholar
Babinsky, H. & Harvey, J. K. 2011 Shock Wave–Boundary-Layer Interactions. Cambridge University Press.Google Scholar
Babinsky, H., Oorebeek, J. & Cottingham, T.2013 Corner effects in reflecting oblique shock-wave/boundary-layer interactions. AIAA Paper 2013-859.Google Scholar
Benek, J. A., Suchyta, C. J. & Babinsky, H.2016 Simulations of incident shock boundary layer interactions. AIAA Paper 2016-0352.Google Scholar
Burton, D. M. F. & Babinsky, H. 2012 Corner separation effects for normal shock wave/turbulent boundary layer interactions in rectangular channels. J. Fluid Mech. 707, 287–306.Google Scholar
Colliss, S. P.2014 Vortical structures on three-dimensional shock control bumps. PhD thesis, University of Cambridge.Google Scholar
Colliss, S. P., Babinsky, H., Nübler, K. & Lutz, T. 2014 Joint experimental and numerical approach to three-dimensional shock control bump research. AIAA J. 52 (2), 436–446.Google Scholar
Délery, J. M. & Dussauge, J.-P. 2009 Some physical aspects of shock wave/boundary layer interactions. Shock Waves 19 (6), 453–468.Google Scholar
van Driest, E. R. 1951 Turbulent boundary layer in compressible fluids. J. Aeronaut. Sci. 18 (3), 145–160.Google Scholar
Eagle, W. E. & Driscoll, J. F. 2014 Shock wave–boundary layer interactions in rectangular inlets: three-dimensional separation topology and critical points. J. Fluid Mech. 756, 328–353.Google Scholar
Musker, A. J. 1979 Explicit expression for the smooth wall velocity distribution in a turbulent boundary layer. AIAA J. 17 (6), 655–657.Google Scholar
Perry, A. E. & Hornung, H. 1984 Some aspects of three-dimensional separation. II. Vortex skeletons. Z. Flugwiss. Weltraumforsch. 8, 155–160.Google Scholar
Squire, L. C. 1961 The motion of a thin oil sheet under the steady boundary layer on a body. J. Fluid Mech. 11 (2), 161–179.Google Scholar
Sun, C.-C. & Childs, M. E. 1973 A modified wall wake velocity profile for turbulent compressible boundary layers. J. Aircraft 10 (6), 381–383.Google Scholar
Titchener, N., Colliss, S. & Babinsky, H. 2015 On the calculation of boundary-layer parameters from discrete data. Exp. Fluids 56 (8), 1–18.Google Scholar
Wang, B., Sandham, N. D., Hu, Z. & Liu, W. 2015 Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects. J. Fluid Mech. 767, 526–561.Google Scholar