Article contents
Convection from a line-source into a two-layer stratified ambient fluid
Published online by Cambridge University Press: 28 March 2017
Abstract
We experimentally investigate the behaviour of a line-source plume falling through a finite two-layer stratified ambient where the depth of the upper ambient layer increases in time. Laboratory observations suggest one of two possible flow regimes depending on the value of 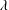 $\unicode[STIX]{x1D706}$, which represents the relative loss of buoyancy experienced by the plume upon crossing the ambient interface. When
$\unicode[STIX]{x1D706}$, which represents the relative loss of buoyancy experienced by the plume upon crossing the ambient interface. When 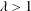 $\unicode[STIX]{x1D706}>1$, a classical filling-box-type flow is realized and plume fluid always reaches the bottom boundary. By contrast, when
$\unicode[STIX]{x1D706}>1$, a classical filling-box-type flow is realized and plume fluid always reaches the bottom boundary. By contrast, when 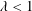 $\unicode[STIX]{x1D706}<1$, we observe a transition by which an increasing fraction of plume fluid discharges along the interface. The approximate start time,
$\unicode[STIX]{x1D706}<1$, we observe a transition by which an increasing fraction of plume fluid discharges along the interface. The approximate start time, 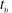 $t_{v}$, and end time,
$t_{v}$, and end time, 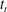 $t_{t}$, of the transition process are well determined by
$t_{t}$, of the transition process are well determined by 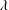 $\unicode[STIX]{x1D706}$. After transition, the ambient density evolves to form a three-layer fluid with an intermediate layer that grows in time. Measured densities of the intermediate layer in experiments with
$\unicode[STIX]{x1D706}$. After transition, the ambient density evolves to form a three-layer fluid with an intermediate layer that grows in time. Measured densities of the intermediate layer in experiments with 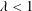 $\unicode[STIX]{x1D706}<1$ are well predicted using plume theory. We further characterize the horizontal speed of the intrusion that forms along the ambient interface, the mass of solute present in the intermediate layer at time
$\unicode[STIX]{x1D706}<1$ are well predicted using plume theory. We further characterize the horizontal speed of the intrusion that forms along the ambient interface, the mass of solute present in the intermediate layer at time 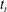 $t_{t}$ and the rate of descent of the intrusion level for
$t_{t}$ and the rate of descent of the intrusion level for 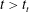 $t>t_{t}$. The significance of our findings is discussed in the context of the ventilation of natural and hybrid ventilated buildings and of effluent discharge through marine outfall diffusers.
$t>t_{t}$. The significance of our findings is discussed in the context of the ventilation of natural and hybrid ventilated buildings and of effluent discharge through marine outfall diffusers.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 4
- Cited by



