Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T14:13:47.195Z Has data issue: false hasContentIssue false
  • English
  • Français

Convection at an isothermal wall in an enclosure and establishment of stratification

Published online by Cambridge University Press:  23 June 2016

T. Caudwell ,
J.-B. Flór  and
M. E. Negretti
T. Caudwell
Affiliation:
Univ. Grenoble Alpes, CNRS, LEGI, 38000 Grenoble, France
J.-B. Flór*
Affiliation:
Univ. Grenoble Alpes, CNRS, LEGI, 38000 Grenoble, France
M. E. Negretti
Affiliation:
Univ. Grenoble Alpes, CNRS, LEGI, 38000 Grenoble, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this experimental–theoretical investigation, we consider a turbulent plume generated by an isothermal wall in a closed cavity and the formation of heat stratification in the interior. The buoyancy of the plume near the wall and the temperature stratification are measured across a vertical plane with the temperature laser induced fluorescence method, which is shown to be accurate and efficient (precision of 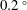$0.2\,^{\circ }$C) for experimental studies on convection. The simultaneous measurement of the velocity field with particle image velocimetry allows for the calculation of the flow characteristics such as the Richardson number and Reynolds stress. This enables us to give a refined description of the wall plume, as well as the circulation and evolution of the stratification in the interior. The wall plume is found to have an inner layer close to the heated boundary with a laminar transport of hardly mixed fluid which causes a relatively warm top layer and an outer layer with a transition from laminar to turbulent at a considerable height. The measured entrainment coefficient is found to be dramatically influenced by the increase in stratification of the ambient fluid. To model the flow, the entrainment model of Morton, Taylor & Turner (Proc. R. Soc. Lond. A, vol. 234 (1196), 1956, pp. 1–23) has first been adapted to the case of an isothermal wall. Differences due to their boundary condition of a constant buoyancy flux, modelled with salt by Cooper & Hunt (J. Fluid Mech., vol. 646, 2010, pp. 39–58), turn out to be small. Next, to include the laminar–turbulent transition of the boundary layer, a hybrid model is constructed which is based on the similarity solutions reported by Worster & Leitch (J. Fluid Mech., vol. 156, 1985, pp. 301–319) for the laminar part and the entrainment model for the turbulent part. Finally, the observed variation of the global entrainment coefficient, which is due to the increased presence of an upper stratified layer with a relatively low entrainment coefficient, is incorporated into both models. All models show reasonable agreement with experimental measurements for the volume, momentum and buoyancy fluxes as well as for the evolution of the stratification in the interior. In particular, the introduction of the variable entrainment coefficient improves all models significantly.

JFM classification

Convection: Convection in cavities Convection: Plumes/thermals Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , pp. 448 - 475
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. 2002 Two-dimensional plumes in stratified environments. J. Fluid Mech. 471, 315–337.CrossRefGoogle Scholar
Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37 (1), 51–80.CrossRefGoogle Scholar
Bejan, A. & Lage, J. L. 1990 The Prandtl number effect on the transition in natural convection along a vertical surface. Trans. ASME J. Heat Transfer 112, 787–790.CrossRefGoogle Scholar
Bruchhausen, M., Guillard, F. & Lemoine, F. 2005 Instantaneous measurement of two-dimensional temperature distributions by means of two-color planar laser induced fluorescence (PLIF). Exp. Fluids 38 (1), 123–131.CrossRefGoogle Scholar
Caudwell, T.2015 Convection et stratification induites par une paroi chauffante: mesures expérimentales et modélisations. PhD thesis, Université Grenoble Alpes.Google Scholar
Coolen, M. C. J., Kieft, R. N., Rindt, C. C. M. & van Steenhoven, A. A. 1999 Application of 2-D LIF temperature measurements in water using a nd : Yag laser. Exp. Fluids 27 (5), 420–426.CrossRefGoogle Scholar
Cooper, P. & Hunt, G. R. 2010 The ventilated filling box containing a vertically distributed source of buoyancy. J. Fluid Mech. 646, 39–58.CrossRefGoogle Scholar
Coppeta, J. & Rogers, C. 1998 Dual emission laser induced fluorescence for direct planar scalar behavior measurements. Exp. Fluids 25 (1), 1–15.CrossRefGoogle Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448.CrossRefGoogle Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23 (1), 455–493.CrossRefGoogle Scholar
Germeles, A. E. 1975 Forced plumes and mixing of liquids in tanks. J. Fluid Mech. 71, 601–623.CrossRefGoogle Scholar
Hunt, G. R. & van den Bremer, T. S. 2011 Classical plume theory: 1937–2010 and beyond. IMA J. Appl. Maths 76 (3), 424–448.CrossRefGoogle Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.CrossRefGoogle Scholar
Kaye, N. B. 2008 Turbulent plumes in stratified environments: A review of recent work. Atmos.-Ocean 46 (4), 433–441.CrossRefGoogle Scholar
Kaye, N. B. & Hunt, G. R. 2007 Overturning in a filling box. J. Fluid Mech. 576, 297–323.CrossRefGoogle Scholar
Linden, P. F. 1999 The fluid mechanics of natural ventilation. Annu. Rev. Fluid Mech. 31 (1), 201–238.CrossRefGoogle Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. P. R. Soc. Lond. A 234 (1196), 1–23.Google Scholar
Nakajima, T., Utsunomiya, M. & Ikeda, Y. 1991 Simultaneous measurement of velocity and temperature of water using LDV and fluorescence technique. In Applications of Laser Techniques to Fluid Mechanics, pp. 34–53. Springer.CrossRefGoogle Scholar
Petracci, A., Delfos, R. & Westerweel, J. 2006 Combined PIV/LIF measurements in a Rayleigh–Bénard convection cell. In 13th International Symposia on Application of Laser Techniques to Fluid Mechanics, Springer.Google Scholar
Sakakibara, J., Hishida, K. & Maeda, M. 1993 Measurements of thermally stratified pipe-flow using image-processing techniques. Exp. Fluids 16 (2), 82–96.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.CrossRefGoogle Scholar
Steven, D. S. & Gregory, F. L.-S. 2011 Transient buoyancy-driven ventilation: part 1. modelling advection. Build. Environ. 46 (8), 1578–1588.Google Scholar
Tsuji, T. & Nagano, Y. 1988 Characteristics of a turbulent natural convection boundary layer along a vertical flat plate. Intl J. Heat Mass Transfer. 31 (8), 1723–1734.CrossRefGoogle Scholar
Walker, D. A. 1987 A fluorescence technique for measurement of concentration in mixing liquids. J. Phys. E: Sci. Instrum. 20 (2), 217–224.CrossRefGoogle Scholar
Wells, A. J. & Worster, M. G. 2008 A geophysical-scale model of vertical natural convection boundary layers. J. Fluid Mech. 609, 111–137.CrossRefGoogle Scholar
Wells, M. G., Griffiths, R. W. & Turner, J. S. 1999 Competition between distributed and localized buoyancy fluxes in a confined volume. J. Fluid Mech. 391, 319–336.CrossRefGoogle Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42 (1), 391–412.CrossRefGoogle Scholar
Worster, M. G. & Huppert, H. E. 1983 Time-dependent density profiles in a filling box. J. Fluid Mech. 132, 457–466.CrossRefGoogle Scholar
Worster, M. G. & Leitch, A. M. 1985 Laminar free-convection in confined regions. J. Fluid Mech. 156, 301–319.CrossRefGoogle Scholar